Процесс нелинейной трансформации гравитационной поверхностной волны на мелкой воде рассматривается в работах многих авторов [1–3, 6–8, 10–11, 14]. Этот процесс, приводящий к опрокидыванию волны и последующему образованию ударной волны (бора), часто наблюдается в прибрежной зоне моря и при вхождении приливной волны в устье реки [4, 13]. Динамика самой обрушенной волны изучена меньше. Аналитические результаты известны для развитого бора, в котором скорости течения по обе стороны от скачка стремятся к константам [1, 8, 10]. Часто при подходе волн к крутому береговому склону имеет место взаимодействие падающей и отраженной волн, которое еще не рассматривалось в литературе. Именно эта проблема изучается в данной статье.
Математическая модель
Гиперболическая система уравнений нелинейной теории мелкой воды имеет вид [1, 8, 10]
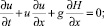
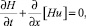(1)
где H(x, t) = h + h(x, t) – полная глубина, отсчитываемая от дна; h(x ,t) – возмущение водной поверхности над невозмущенной глубиной бассейна h; u – усредненная по глубине горизонтальная скорость водного потока; g – ускорение силы тяжести. В данной работе система уравнений (1) решается численно с помощью программного пакета CLAWPACK (www.amath.washington.edu/~claw), использующего метод конечных объемов [12]. Глубина бассейна h постоянна и во всех расчетах выбрана равной 1 м. Граничные условия на границах расчетной области соответствуют свободному уходу волны через границу. Размер пространственного шага – 0,5 м, временного – 2 с. Начальные условия соответствуют двум римановым волнам, двигающимся навстречу друг другу:
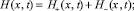
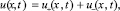(2)
где 
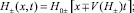
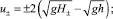
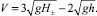(3)
В начальный момент времени уединенные волны расположены симметрично относительно начала координат на расстоянии 2,6 км друг от друга. Форма уединенной волны выбрана гауссовой
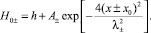(4)
Здесь А± – амплитуды импульсов; l± – их характерные длины; x0 характеризует расстояние от начала координат до каждого из импульсов. В расчетах характерные длины импульсов (λ) выбраны одинаковыми и равными 0,9 км. В численных расчетах контролировалось сохранение массы, и ошибка не превышала 10–6 %.
Взаимодействие двух импульсов
Рассмотрим теперь результаты расчетов с данными начальными условиями. Рис. 1 иллюстрирует процесс взаимодействия двух уединенных волн амплитудой 0,1 м. В этом случае параметр нелинейности, определяемый отношением амплитуды волны к глубине бассейна, достаточно мал (0,1), и столкновение волн произойдет до того, как начнут образовываться ударные фронты.
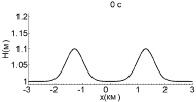
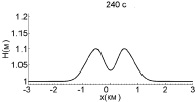
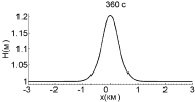
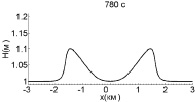
Рис. 1. Взаимодействие двух уединенных волн с амплитудой 0,1 м (слабонелинейный случай)
В численном эксперименте максимум амплитуды при взаимодействии волн составил 0,2 м, что хорошо согласуется с линейной теорией. Взаимодействие римановых волн одинаковой амплитуды исследовалось аналитически также в работе 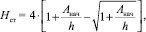[5]
(5)
где Aнач – амплитуда волны непосредственно перед столкновением. В момент взаимодействия высота результирующей волны Hст оценивается в 0,2 м по формуле (5), что полностью соответствует результатам численного эксперимента. Зависимость максимального значения поля от времени демонстрирует рис. 2, из которого видно, что падение амплитуды, связанное с возникновением скачка, началось только с момента времени Т ~ 1600 с. Этот факт еще раз подтверждает, что взаимодействие римановых волн происходило до образования ударных фронтов.
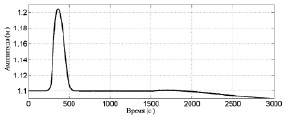
Рис. 2. Зависимость максимального значения толщины потока от времени (А0 = 0,1 м)
Взаимодействие волн большей амплитуды (А = 0,4 м) показано на рис. 3. Здесь волны успевают столкнуться также до того, как образуются ударные фронты (6–7 мин). Максимум смещения в момент взаимодействия составляет 0,87 м, что совпадает с оценкой (5).
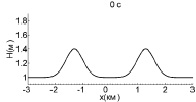
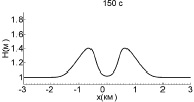
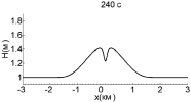
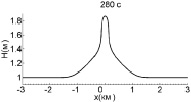
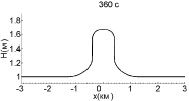
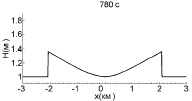
Рис. 3. Взаимодействие двух уединенных волн с амплитудой 0,4 м
Теперь рассмотрим случаи столкновения волн с ударными фронтами (рис. 4). Для этого увеличим амплитуду начальных импульсов до 0,9 м, а расстояние между ними – до 6,6 км. К моменту столкновения ударный фронт на каждой волне успевает сформироваться полностье, и высота волн начинает падать (рис. 5), так что амплитуды обеих волн непосредственно перед взаимодействием равны 0,7 м, то есть на 0,2 м меньше, чем начальные значения.
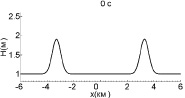
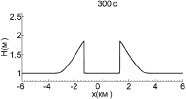
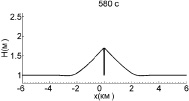
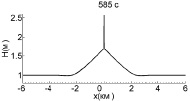
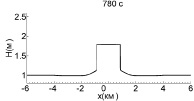
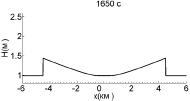
Рис. 4. Взаимодействие двух уединенных волн с начальной амплитудой 0,9 м
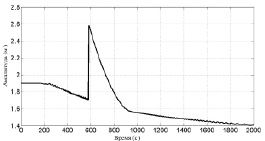
Рис. 5. Зависимость максимальной величины толщины водного потока от времени (A0 = 0,9 м)
Для теоретической оценки высоты «пика» при столкновении ударных волн воспользуемся законами сохранения массы и момента [1, 8, 10]:
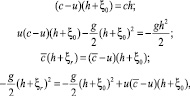(6)
где с – скорость движения подходящего бора; u – скорость потока за фронтом ударной волны; 
– скорость бора после взаимодействия; ξ0 – начальная высота возмущения, а ξr – искомая нами высота потока в момент взаимодействия. Эта система хорошо аппроксимирует случаи взаимодействия ударных волн относительно большой амплитуды (ξ0 ≥ 3h). В случае же бора малой амплитуды поток становится неустойчивым, и для его описания надо пользоваться теорией волнообразного бора [9]. Максимум толщины потока в момент взаимодействия составляет 2,6 м. Если вычесть невозмущенную глубину в 1 м, то получаем оценку высоты волны в момент столкновения 1,6 м. Высота необрушенной волны, вычисляемая по формуле (5) с такими начальными условиями будет равна также 1,6 м, а высота бесконечного бора по формуле (6) – 1,60 м. Линейная же теория предсказывает 1,4 м. Различие с предсказаниями нелинейной теории связано с «переходной» формой ударной волны, которая не может быть описана формой развитого бора. Так как ударный фронт был сформирован до взаимодействия импульсов, то и распределение максимума поля смещения будет иметь форму ассиметричного треугольника. Видно, что обрушение волны, а соответственно и спад амплитуды, начало происходить в момент времени 200 с, тогда как столкновение волн произошло только спустя 590 с.
Заключение
В работе исследованы случаи взаимодействия уединенных поверхностных гравитационных волн положительной полярности на поверхности жидкости малой глубины. Рассчитаны максимумы смещения водной поверхности в момент взаимодействия ударных волн. При малых амплитудах рассчитанные величины хорошо описываются результатами аналитической теории для взаимодействующих римановых волн. В случае обрушения из-за диссипации энергии на фронте ударных волн толщина потока становится меньшей, чем предсказывается теорией для римановых волн и полностью развитого бора.
Представленные результаты научно-исследовательской работы получены в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы, а также при поддержке грантов МК1440.2012.5, РФФИ 11-05-970006, SF0140007s11 и ETF8870.
Рецензенты:Петрухин Н.С., д.ф.-м.н., профессор кафедры математики, Высшая школа экономики, г. Нижний Новгород;
Талипова Т.Г., д.ф.-м.н., ведущий научный сотрудник, Институт прикладной физики РАН, г. Нижний Новгород.
Работа поступила в редакцию 26.10.2012.