Некоторые результаты рассматриваемого численного метода приведены в следующих работах [1–10].

Поставленная задача реализуется с помощью уравнений математической нестационарной динамической теории упругости.

Для решения поставленной задачи рассмотрим некоторое тело Γ в прямоугольной декартовой системе координат OXY, которому в начальный момент времени t = 0 сообщается механическое воздействие.

Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид

(x, y) ∈ Γ;

(x, y) ∈ (Γ ∪ S), (1)

где σx, σy и τxy – компоненты тензора упругих напряжений; εx, εy и γxy – компоненты тензора упругих деформаций; u и v – cоставляющие вектора упругих перемещений вдоль осей OX и OY соответственно; ρ – плотность материала; – скорость продольной упругой волны; – скорость поперечной упругой волны; v – коэффициент Пуассона; E – модуль упругости; S (S1 ∪ S2) – граничный контур тела Γ.

Систему (1) в области, занимаемой телом Γ, следует интегрировать при начальных и граничных условиях.

Начальные условия в области Γ зададим в виде

(x, y) ∈ Γ , (2)

где u0, v0, и – заданные в области Γ функции.

Граничные условия зададим в виде:

• составляющих компонентов тензора упругих напряжений на границе S1

(x, y) ∈ S1; (3)

• составляющих компонентов вектора упругих перемещений на границе S2

u = Bx; v = By;, , (x, y) ∈ S2, (4)

где l и m – направляющие косинусы; Ax, Ay, Bx и By – заданные на границе S функции.

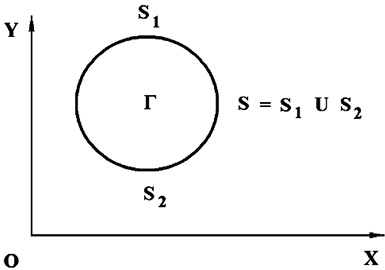
Рис. 1. Некоторое тело Γ в прямоугольной декартовой системе координат OXY

Для решения двумерной нестационарной динамической задачи математической теории упругости с начальными и граничными условиями (1–4) используем метод конечных элементов в перемещениях.

Задача решается методом сквозного счета, без выделения разрывов. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений.

Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Γ, записываем приближенное значение уравнения движения в теории упругости

(5)

где – матрица инерции; – матрица жесткости; – вектор узловых упругих перемещений; – вектор узловых упругих скоростей перемещений; – вектор узловых упругих ускорений; – вектор узловых упругих внешних сил.

Соотношение (5) − система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.

Таким образом, с помощью метода конечных элементов в перемещениях линейную задачу с начальными и граничными условиями (1–4) привели к линейной задаче Коши (5).

Для интегрирования уравнения (5) конечноэлементным вариантом метода Галеркина приведем его к следующему виду

(6)

Интегрируя по временной координате соотношение (6) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек

(7)

где Δt– шаг по временной координете.

Определим упругое контурное напряжение на границе области, свободной от нагрузок.

С помощью вырождения прямоугольного конечного элемента с четырьмя узловыми точками получим контурный конечный элемент с двумя узловыми точками (рис. 2).

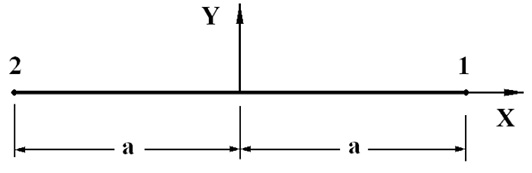
Рис. 2. Контурный конечный элемент с двумя узловыми точками

При повороте оси x на угол α против часовой стрелки получим упругое контурное напряжение σk в центре тяжести контурного конечного элемента с двумя узловыми точками

(8)

Рассмотрим устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках

(i = 1, 2, 3, ...), (9)

где Δl – длина стороны конечного элемента.

Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках.

Для исследуемой области, состоящей из материалов с разными физическими свойствами, выбирается минимальный шаг по временной координате.

На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при взрывных воздействиях на уникальные сооружения.

При разработке комплекса программ использовался алгоритмический язык Фортран-90.

Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений.

Автор выражают благодарность Мусаеву В.К. за внимание к работе.

Рецензенты:

Мусаев В.К. Оглы, д.т.н., профессор, директор научно-производственной фирмы «Интерсейм», г. Пушкино;

Шаршак В.К., д.т.н., профессор кафедры «Механика, машины и оборудование пищевых производств» Донского государственного аграрного университета, г. Новочеркасск.

Работа поступила в редакцию 18.10.2012.