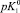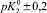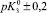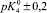Кислотно-основные свойства оксидных фаз, полностью соответствующие модели Грэма-Парсонса, позволяют характеризовать особенности строения двойного электрического слоя (ДЭС) на границе оксид-электролит, а также описывать особенности адсорбции ионов на поверхности оксида [2–7].
Существующие классические модели, такие, как Лэнгмюра, Фрейндлиха, Фрумкина, широко используемые на практике для описания адсорбционных явлений, не позволяют учитывать особенности влияния строения ДЭС на специфику адсорбции ионов [2]. Наиболее перспективным направлением является использование вириальных изотерм адсорбции в координатах
.
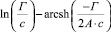Экспериментальная часть
Для изучения адсорбции ионов использовались продажные оксиды железа (Fe3O4 и α-Fe2O3) квалификации «ХЧ» (фракция 20–50 мкм) после дополнительной промывки от сопутствующих ионов и просушивания при 120 °С в течение 4 часов в инертной атмосфере аргона. Идентификация оксидов была проведена методами ИК-спектроскопии и РФА, которые доказали наличие монокристаллической фазы в образцах. Удельная поверхность, определенная методом БЭТ, составила в зарядовых единицах для Fe3O4 и α-Fe2O3 соответственно 62 и 42 мкКл/см2. Рабочие растворы готовились на бидистиллированной воде из NaCl квалификации «ХЧ» после дополнительной перекристаллизации, регуляция рН осуществлялась добавлением HCl или 40 % NaOH. Определение концентраций хлорид- и ионов натрия проводилось при помощи ионселективных электродов на рН-метр-иономере «Эксперт-001-3-0.1» в термостатируемой ячейке (303 К, 1 г оксида/50 мл раствора) в атмосфере аргона. Результаты измерений представлены на рис. 1.
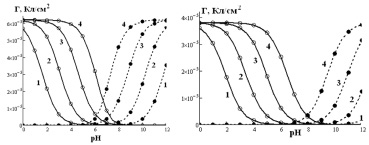
Рис. 1. Зависимость адсорбции хлорид-анионов () и катионов натрия () от рН на Fe3O4 (слева) и α-Fe2O3 (справа) при различной концентрации NaCl, моль/л: 1 – 0,001; 2 – 0,01; 3 – 0,1; 4 – 1 (точки – экспериментальные данные, линии – аппроксимирующие кривые)
Величина заряда q0 на поверхности оксида компенсируется противоионами (хлорид-ионами при рН < рН0 и катионами натрия при рН > рН0), образующими заряд q1 во внутренней плоскости Гельмгольца, проходящей через центры дегидратированных ионов, а также суммарным зарядом ионов в диффузном слое q2 (внешняя плоскость Гельмгольца):
Используя данные по адсорбции хлорид- и ионов натрия при различных рН и концентрациях электролита, можно рассчитать величину заряда q1:
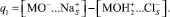(1)
Величины зарядов q1 от функции (рН-рН0) для различных концентраций электролита приведены на рис. 2. Из условия электронейтральности, учитывая уравнение Нернста и сделав ряд преобразований, можно получить уравнение (2), позволяющее рассчитать q0 (рис. 3).
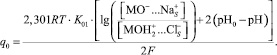(2)
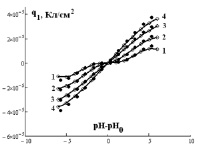
Рис. 2. Зависимость q1 от (рН–рН0) для Fe3O4 (черные точки) и α-Fe2O3 (белые точки) при различной концентрации NaCl, моль/л: 1 – 0,001; 2 – 0,01; 3 – 0,1; 4 – 1 (точки – экспериментальные данные, линии – аппроксимирующие кривые)
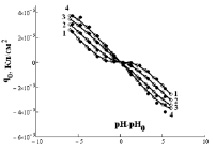
Рис. 3. Зависимость q0 от (рН–рН0) для Fe3O4 (черные точки) и α-Fe2O3 (белые точки) при различной концентрации NaCl, моль/л: 1 – 0,001; 2 – 0,01; 3 – 0,1; 4 – 1 (точки – экспериментальные данные, линии – аппроксимирующие кривые)
Экспериментальная зависимость q2 от (рН – рН0) имеет значительный разброс для различных оксидов в области сильнокислых и сильнощелочных рН, связанный с небольшими значениями заряда и погрешностью расчета.
Дальнейшая методика расчета констант кислотно-основных равновесий аналогична таковой для зависимости электрокинетического потенциала от рН [2]. Приведенные результаты показывают, что использование зависимости адсорбции хлорид- и ионов натрия от рН позволяет рассчитать величины зарядов, возникающих на границе оксид металла/раствор. Важно отметить, что их величина слабо зависит от природы оксида, если расчетные данные представить в координатах q – (рН – pH0), и характеристики оксидных фаз определяются только рН нулевого заряда [1]. На основании адсорбционных данных были рассчитаны константы кислотно-основных равновесий на границе оксид-электролит, которые показали хорошее согласование с рассчитанными по предыдущим методикам [2] (табл. 1).
Таблица 1
Результаты расчета значений констант равновесий из зависимости адсорбции хлорид- и ионов натрия от рН
|
Оксиды железа |
|
|
|
|
рHтнз ± 0,2 |
|
Fe3O4 |
4,4 |
9,0 |
6,2 |
7,0 |
6,6 |
|
α–Fe2O3 |
6,23 |
10,25 |
8,20 |
8,28 |
8,24 |
Адсорбция анионов (ГСl–) осуществляется в плотной части ДЭС, имеющей заряд q1 и потенциал ψ1, и описывается уравнением 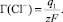(3).
(3)
Принимая, что Г(Cl–) пропорционально сi и учитывая уравнение (1), можно найти зависимости Г(Cl–) от ψ1:
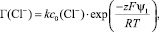(4)
где k – константа адсорбционного равновесия.
Зависимость суммарного заряда q1 адсорбированных на границе магнетит/водный раствор KCl катионов и анионов от концентрации электролита с0(Сl–) и среднего значения потенциала внутренней плоскости Гельмгольца ψ1 может быть аппроксимирована следующим уравнением:
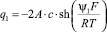
или
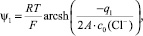(5)
где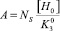 
, [H0] – концентрация ионов водорода на поверхности оксида при рН0.
Рассматривая адсорбцию хлорид-ионов в плоской части ДЭС и подставив (5) в (4), получим уравнение вида:
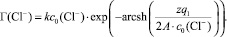(6)
Прологарифмировав уравнение (6) и сделав ряд преобразований, найдем:
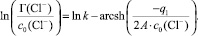(7)
Для экспериментальной проверки используется уравнение (7), графическое изображение которого в координатах
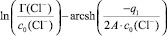
представляет прямую (рис. 4).
Из анализа данных следует, что величина ln(k) (первый вириальный коэффициент) не зависит от рН и концентрации электролита, незначительно зависит от природы оксида; их значение представлено в табл. 2.
Таблица 2
Значения рК адсорбции уравнения (7) для оксидов железа
|
Fe3O4 |
9,36 |
|
α-Fe2O3 |
9,25 |
|
γ-Fe2O3 |
9,77 |
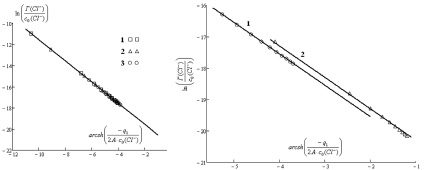
а б
Рис. 4. Зависимость : а – для магнетита (с (NaCl) = 0,001 – 1 М, Т = 298 К) при различных значениях рН: 1–3; 2–4; 3–5; б – для оксидов железа: 1 – Fe3O4; 2 – α-Fe2O3 (с (NaCl) = 0,001–1 М, рН = 5, Т = 298 К
Выводы
На основании теории Грэма-Парсонса предложена модель, описывающая адсорбцию однозарядных ионов на оксидной поверхности с учетом параметров ДЭС. Константа полученного уравнения не зависит от концентрации фонового электролита и рН раствора, однако зависит от природы оксида. Физический смысл полученной константы и ее связь с физико-химическими характеристиками оксидов металлов являются предметом дальнейших исследований.
Работа выполнена при финансовой поддержке ГК № 16.740.11.0679.
Рецензенты:
Ярополов А.И., д.х.н., профессор, заведующий лабораторией Федерального государственного учреждения науки Института биохимии им. А.Н. Баха Российской академии наук, г. Москва;
Графкина М.В., д.т.н., профессор, заведующий кафедрой «Экологическая безопасность автомобильного транспорта» Московского государственного машиностроительного университета (МАМИ), г. Москва.
Работа поступила в редакцию 04.04.2012