В работе пойдёт речь о синтезе четырёх различных видах кинематических цепей. Будем иметь в виду, что кинематической цепью принято называть последовательное соединение звеньев кинематическими парами. Рассмотрим вопрос о методах синтеза кинематических цепей в хронологическом порядке, т.е. по времени публикации их в научной печати.
Первый научный подход в решении вопроса о создании метода синтеза шарнирных механизмов предпринял русский ученый математик П.Л. Чебышёв. Посетив в 1852 г. Англию и ознакомившись с работой паровых машин Дж. Уатта, он в своём отчете о путешествии за границу [14] написал: «…Мы не знаем, каким путем он дошел до наивыгоднейшей формы своего механизма и размеров его элементов. Правила, которым следовал Уатт при устройстве параллелограммов, могли служить руководством для практики только до тех пор, пока не встречалась необходимость изменить форму его; а с изменением формы этого механизма потребовались новые правила…». Заинтересовавшись вопросом создания подобных механизмов, после возвращения из командировки по странам Европы П.Л. Чебышёв занялся исследованием параллелограммных механизмов, используя методы математического анализа, и установил связь между числом звеньев, числом кинематическим и подвижностью механизма.
Основываясь в своих исследованиях на формуле П.Л. Чебышёва, М.Ф. Грюблер в 1883 г. нашел важным рассмотреть структуры, обладающие подвижностью W = 4, т.е. такие, в которых нет свободных кинематических пар (замкнутые, принуждённые цепи) и которые имеют в плоскости четыре подвижности, три – совместных для всей цепи в плоскости и одну – относительного движения звеньев. Впоследствии такие цепи получили название цепей Грюблера. При остановке одного из звеньев в такой цепи она становится цепью с W = 1, называемой механизмом [17].
В начале прошлого века (1916 г.) русский учёный Л.В. Ассур обосновал другой принцип построения механизмов [1], который был сформулирован так: механизм может быть создан путём присоединения к ведущему звену группы или групп звеньев, обладающих нулевой подвижностью W = 0. Именно такие группы звеньев в дальнейшем стали называть группами Ассура.
В 1952 г. Баранов Г.Г. предложил метод нахождения групп Ассура, в основу которого положено создание жесткой, замкнутой, неизменяемой группы звеньев с W = 3, названной им «фермой», который заключается в последовательном отбрасывании одного из звеньев «фермы» [3]. Однако М. Грюблер не оставил правил создания собственно цепей с W = 4, Л.В. Ассуром не был разработан метод структурного построения самих групп Асура, за исключением нормальных групп, а Г.Г. Баранов не представил каких-либо рекомендаций по поиску самих «ферм». Рассмотрим более подробно выше перечисленные методы синтеза шарнирных кинематических цепей.
Метод синтеза структур механизмов П.Л. Чебышёва
Приступив к решению поставленной задачи, П.Л. Чебышев отмечает существование только трех видов параллелограммов (сокращенный, полный параллелограмм Уатта и механизм Эванса), которые широко применялись при создании машин того времени, и говорит о том, что составить различных параллелограммов, дающих прямолинейное движение с приближением, по желанию большим, чем вторая степень, можно достаточно много. Здесь речь идет о таких параллелограммах, степень точности которых легко определяется, и для перехода от бесконечно малых движений к конечным необходимо только изменить размеры их частей. Эти изменения незначительные и могут быть получены с помощью рядов по способу, приведенному в мемуаре «Теория механизмов, известных под названием параллелограммов» [15].
В тех случаях, когда необходимо создать параллелограммный механизм, заменяющий своими частями мотыль и кривошип, ряды не могут быть использованы, т.к. в этом случае нельзя говорить о бесконечно малых движениях. Такие механизмы П.Л. Чебышёв предлагает рассматривать «как систему прямых линий, двигающихся в одной плоскости и связанных между собою шарнирами, которые препятствуют точкам соединения линий скользить по ним, но не мешают изменяться углам, составленным этими линиями». При этом некоторые из линий должны быть прикреплены к плоскости, вокруг которых они могут вращаться. Обозначая m – число линий, образующих параллелограмм, n – число шарниров, связывающих эти линии по две, ν – число точек прикрепления и указывая на то, что на плоскости каждая из m линий определяется тремя величинами (двумя координатами и углом наклона её к оси абсцисс), а ν – двумя (координаты точки прикрепления), то в любой рассматриваемой системе место всех точек будет определяться 3m величинами, связанными между собой 2(n + ν) уравнениями, а число независимых переменных представится разностью [15]
3m – 2(n + ν).
Для того чтобы точки рассматриваемой системы могли совершать вполне определенные движения, как в механизмах, эта разность должна быть равна 1, т.е.
3m – 2(n + ν) = 1.
В современных обозначениях формула П.Л. Чебышёва запишется так:
3n – 2(p5 + ν) = W, (1)
где n – число подвижных звеньев механической системы; р5 – число подвижных шарниров; ν – число неподвижных шарниров; W – подвижность механической системы, для механизмов W = 1.
Понимая, что для создания всего многообразия параллелограммных механизмов, удовлетворяющих необходимым требованиям движения, одной полученной формулы недостаточно, П.Л. Чебышёв в работе [15] приводит еще одну формулу. Она основана на том, что, во-первых, любая механическая система может совершать определенное движение в плоскости, только при наличии точек прикрепления, т.е. ν > 0, а во-вторых, число шарниров р5 должно быть больше (n – 2). Тогда из уравнения (1) при условии р5 > (n – 2) получается, что число неподвижных кинематических пар (стоек) должно удовлетворять условию
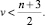 (2)
(2)
Рассмотрим пример, позволяющий понять способ создания П.Л. Чебышёвым различных схем параллелограммных механизмов, применяя формулу (1) и зависимость (2). При n = 5 и W = 1, по (1) р5 + ν = 7, а по (2) ν < 4. При этих условиях возможно существование трех вариантов решений:
1. ν = 1, р5 = 6;
2. ν = 2, р5 = 5;
3. ν = 3, р5 = 4.
Создать работоспособный механизм по первому варианту, с одной неподвижной кинематической парой невозможно, так как в этом случае получается жесткая неизменяемая механическая система, способная только совершать вращение вокруг стойки (рис. 1, а).
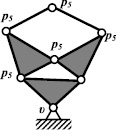
Механизм, полученный при условии ν = 2, р5 = 5, приведен на рис. 1, б. Найденные в нём соотношения длин звеньев позволили П.Л. Чебышёву получить прямолинейное движение точки А с точностью до шестой степени. Самое большое количество параллелограммных механизмов в работе [15], дающих различную степень точности прямолинейного движения определенной точки, было получено при значениях n = 5, ν = 3, р5 = 4.
 б
б 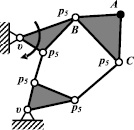
 г
г 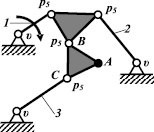
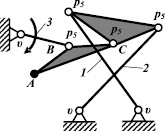
Рис. 1. Параллелограммные механизмы с пятью подвижными звеньями с одной (а), с двумя (б) и тремя (в, г) неподвижными кинематическими парами
Для примера приведем два характерных параллелограмма. Механизм, представленный на рис. 1, в, состоящий из тех же звеньев, что и механизм на рис. 1, г, обеспечивает прямолинейность движения точки А с точностью до восьмой степени, а на рис. 1, г (где звенья 1 и 2 перекрещиваются между собой) – с точностью до тринадцатой степени.
Из приведенных примеров видно, что различие в расположении неподвижных кинематических пар, около которых совершают движения подвижные звенья, одно их которых содержит определенную точку, например, точку А, влияет на точность её прямолинейного движения. Созданием именно таких механических систем занимался П.Л. Чебышёв. При внимательном изучении параллелограммных механизмов, представленных на рис. 1, б и в, г, можно заметить, что они являются шестизвенными механизмами. Звенья ВС по сути являются линейными, но конструктивно выполнены так, что вместо третьей кинематической пары находится точка, двигающаяся по определенной траектории.
Таким образом, рассматривая вопрос о создании параллелограммных механизмов, которые максимально приближают движение определенной точки к прямолинейному движению, П.Л. Чебышев решил не только задачу о приближении функций многочленами, приведшую к созданию теории наилучшего приближения функций; но и вывел формулу, устанавливающую связь между числом линий (числом звеньев), числом шарниров (числом кинематических пар), соединяющих эти линии по две, и подвижностью механизма, получившей впоследствии название формулы подвижности Чебышёва. Однако необходимо отметить, что использовать метод П.Л. Чебышева при синтезе структурных схем плоских сложных шарнирных механизмов практически невозможно, т.к. нельзя определить число и сложность звеньев, формирующих механизм.
Метод синтеза механизмов по М. Грюблеру
Основополагающей работой, в которой обосновывается метод синтеза плоских шарнирных механизмов, является научная статья М.Ф. Грюблера [17], опубликованная им в 1883 г. и, по видимому, впервые переведенная на русский язык в 2009 г. [6]. К этому году была известна структурная формула подвижности Чебышёва П.Л., обоснованная им в 1869 г., на что и указывает в [17] М. Грюблер и предлагает рассмотреть кинематические цепи, которые удовлетворяют условию
3nГ – 2р5 = 4, (3)
где nГ – число звеньев цепи Грюблера.
Например, если соединить шарнирами четыре звена так, как это показано на рисунке 2, то, в соответствии с формулой Чебышёва (1), эта цепь будет иметь подвижность W = 3∙4 – 2∙4 = 4.
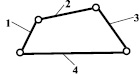
Рис. 2. Четырёхзвенная замкнутая кинематическая цепь Грюблера
Кинематическая цепь, показанная на рис. 2, есть простейшая кинематическая цепь Грюблера. Если теперь начать останавливать звенья 1, 2, 3 или 4, можно получать разные механизмы – двухкривошипные, кривошипно-коромысловые или двухкоромысловые. При этом структурно они отличаться друг от друга не будут – все они шарнирные четырёхзвенники.
Таким образом, если в цепи с W = 4 остановить одно из звеньев, т.е. сделать его неподвижным, то остальные звенья получат вполне определенные движения, а замкнутая кинематическая цепь в случае, когда число подвижных звеньев определяется как n = nГ – 1, становится механизмом, и подвижность её согласно формуле Чебышёва (1) будет равна единице W = 3∙3 – 2∙4 = 1.
Кроме того, в работе [17] М. Грюблером введено понятие i-парных звеньев и отмечено, что кинематические цепи могут содержать в своем составе различные по сложности звенья, в современной терминологии называемые линейными или двухпарными (n2), треугольными или трехпарными (n3), четырёхугольными или четырехпарными (n4) и т.д. (рис. 3).

Рис. 3. Звенья различной сложности
А также показано, что число кинематических пар и число звеньев цепи описываются следующими уравнениями
2p5 = 2n2 + 3n3 + 4n4 + ..., (4)
nГ = n2 + n3 + n4 + ... . (5)
Рассмотрим принцип метода синтеза шарнирных механизмов по Грюблеру на примере цепи, изображенной на рис. 4. Число звеньев по Грюблеру nГ = 6, число шарниров р5 = 7, подставляя эти значения в (1), получим W = 3·6 – 2·7 = 4. При остановке одного звена число подвижных звеньев n = 5, р5 = 7, подвижность по (1) W = 3·5 – 2·7 = 1.
Механизм, приведенный на рис. 4, б, получен при остановке одного из звеньев цепи Грюблера (рис. 4, а), приведенных под номерами 1, 3, 4 и 6, а на рис. 4, в – звеньев 2 или 5, т.е. из такой цепи Грюблера получается два различных по структуре шарнирных механизма. Необходимо отметить, что синтез самих цепей с W = 4, М. Грюблер не рассматривал, и ни в одной из своих последующих работ вопрос о создании замкнутых принужденных цепей им не ставился. Таким образом, для того чтобы применить рассмотренный метод для синтеза механизмов, необходимо иметь метод, позволяющий создавать сами цепи Грюблера.
а 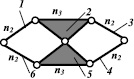 б
б 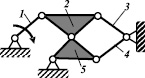 в
в 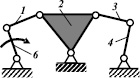
Рис. 4. Метод синтеза шарнирных механизмов по Грюблеру
Ассуров метод синтеза плоских механизмов
Русский ученый Л.В. Ассур, один из основателей русской научной школы по теории механизмов и машин, создал не только рациональную классификацию плоских шарнирных механизмов, но и предложил метод создания таких механизмов.
В 1916 г. Л.В. Ассур писал: «Единственный общий приём образования новых механизмов состоит в том, чтобы к двум точкам данного механизма присоединять шарнирно концы двух стержней, два других конца которых также шарнирно между собой соединять». Л.В. Ассур указывает на то, что «в прошлом на этот приём обращал внимание Д.Д. Сильвестр, который предложил называть комбинацию обоих присоединяемых стержней диадой». В своём исследовании [2] Л.В. Ассур описывает более сложную, а именно – четырёхповодковую группу, и указывает, что она также впервые опубликована М.Ф. Грюблером. Зная о существовании диады Сильвестра, трёхповодковом звене Бурместера и четырёхповодковой группе Грюблера, Ассур нашел и развил общий принцип построения нормальных многозвенных групп нулевой подвижности, разработав метод развития поводка, а затем метод создания механизмов путем наслоения нормальных групп, обладающих нулевой подвижностью на механизм первого класса (рис. 5).

Рис. 5. Ассуров метод синтеза плоских шарнирных механизмов
Таким образом, Л.В. Ассур после глубокого анализа накопленного опыта в структуре механизмов пошел по другому пути в отличие от многих других исследователей и, в частности, от Грюблера. Он рассмотрел синтез механизмов через суммирование подвижностей отдельных групп. И показал, что создать сколь угодно сложный механизм можно путем наслоения на ведущее звено (кривошип), имеющее подвижность W = 1, нормальных групп, подвижность которых равна нулю W = 0. До сих пор статически определимые группы звеньев, обладающие нулевой подвижностью, называют группами Ассура. Разработанное Л.В. Ассуром учение о структуре и классификации механизмов получило широкое использование в практике конструирования современных механизмов. Однако вопрос о создании метода, позволяющего получать все многообразие сложных групп Ассура, содержащих изменяемые замкнутые контуры, остается актуальным и в настоящее время, несмотря на известный метод Г.Г. Баранова. Обратимся к нему и рассмотрим более подробно.
В 1939 г. в работе [11] Х.Ф. Кетова и Н.И. Колчина впервые был изложен метод выделения из так называемых «плоских ферм» кинематических цепей нулевой подвижности – групп Ассура и наоборот. Позже, в 1952 г. этот метод был существенно развит Г.Г. Барановым и доведен до практического использования. В работе [3] Г.Г. Баранов обосновывает метод получения групп нулевой подвижности, который основан на создании жестких, неизменяемых групп звеньев («ферм»), подвижность которых W = 3. Из такой созданной «фермы», путем последовательного отбрасывания одного из звеньев, осуществляется синтез групп нулевой подвижности. Покажем этот метод на примере пятизвенной «фермы» (рис. 6, а). Первая группа, группа Бурмейстера, (рис. 6, б) получается при отбрасывании звеньев 2 или 4, а вторая, четырехзвенная группа с изменяемым замкнутым контуром (рис. 6, в) – при удалении звеньев 1, 3 или 5, т.е. из рассмотренной «фермы» получается две структурно отличающиеся друг от друга группы Ассура.
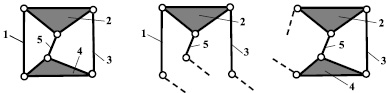
Рис. 6. Метод синтеза групп нулевой подвижности по Баранову
Г.Г. Барановым в [3] приведены: одна трёхзвенная, одна пятизвенная, три семизвенных и двадцать шесть десятизвенных «ферм», из которых получаются четырех, шести и восьмизвенные группы нулевой подвижности. Необходимо также отметить, что найденные им три семизвенные плоские «фермы», позволили вполне доказательно установить десять отличающихся друг от друга шестизвенных групп Ассура, которые ранее найдены В.В. Добровольским без описания метода [5].
В 1988 году в работе [12] профессор Э.Е. Пейсах ставит задачу, целью которой является построение всего многообразия структурных схем одноподвижных механизмов второго класса. Для этого, основываясь на теории графов и на принципе построения механизмов по методу Ассура, для ЭВМ была разработана программа с укрупненной блок-схемой для нахождения кинематических схем таких механизмов. В качестве исходных данных в ЭВМ вводилось число звеньев механизмов, которое одновременно соответствовало числу вершин графа. Результатами расчета являлись неизоморфные графы, которые представлялись либо в матричном, либо в графическом представлении графа типа 1–II высоты h с числом вершин, не превосходящим число звеньев (n) исследуемого механизма [11]. В 2005 г. в работе [13] профессор Пейсах Э.Е. сделал некоторое обобщение по поводу количественного состава структурных схем трёх видов структур, а именно – кинематических цепей Грюблера, групп Ассура и механизмов, в зависимости от числа используемых звеньев.
Считая, что эта таблица является важной вехой в рассматриваемом вопросе, в работе [7] авторами данной статьи предложено назвать эту таблицу «таблицей Пейсаха Э.Е.» и внести в неё как вид структуры – «фермы Баранова», а также указать под видами всех структур соответствующие им подвижности.
Таблица Э.Е. Пейсаха
|
Виды и числа структур |
||||
|
Числа звеньев, n |
Числа кинематических цепей Грюблера, W = 4 |
Числа ферм Баранова для звеньев (n + 1), W = 3 |
Числа групп Ассура, W = 0 |
Числа механизмов, W = 1 |
|
2 |
0 |
1 |
1 |
0 |
|
4 |
1 |
1 |
2 |
1 |
|
6 |
2 |
5 |
10 |
7 |
|
8 |
16 (20) |
26 |
173 (167) |
153 (158) |
В приведенной таблице колонка с числами звеньев структур заполнены лишь частично, т.к. предполагается, что не все цифры, приведённые профессором Э.Е. Пейсахом в [13], вполне подтвердятся дальнейшими исследованиями, но они могут уточняться и сверяться по «таблице Пейсаха». И этому уже на настоящий момент есть доказательство. Так, в работе [8] убедительно показано, что восьмизвенных цепей Грюблера в действительности не 16, а 20, а восьмизвенных механизмов не 153, а 158 [4]. Вопрос о количестве восьмизвенных групп Ассура, указанных в таблице числом 173, подробно рассмотрен и обоснован в [9]. Таким образом, проведенный анализ показывает, что все исследования Пейсаха Э.Е. по поиску структурных схем плоских кинематических цепей целиком основываются на использовании ранее известных методов Л.В. Ассура, М. Грюблера и подхода Г.Г. Баранова.
Таким образом, проведенное исследование показало, что к началу XXI века важная задача – задача синтеза структур механизмов по заданным параметрам осталась не решенной.
В основу решения этой задачи авторами настоящей статьи был положен сформулированный профессором Л.Т. Дворниковым (1994 г.) принцип, на основании которого любые кинематические цепи строятся путем присоединения к наиболее сложному – базисному звену (τ –угольнику) виртуальных звеньев ni, добавляющих в цепь по i кинематических пар [10]. На основе этого принципа для синтеза плоских кинематических цепей была создана обобщенная универсальная структурная система, позволяющая по заданным сложности базисного звена (τ) и подвижности цепи (W) находить полное множество возможных кинематических цепей.
Помимо значений τ и W введены дополнительные параметры, определяющие специфику разыскиваемых цепей, а именно; g – число ветвей цепи; a – число изменяемых замкнутых контуров цепи, d – число выходов цепи; lс – суммарное число сторон цепи; lн/d – распределение числа наружных сторон между выходами цепи.
Наиболее важным нововведением в проблему синтеза структур цепей является разработка алгоритма их поиска, основанного на использовании древа приёмов и критериев, позволяющих выстраивать процедуру отыскивания структур во всём их многообразии без пропуска возможных и без повторений [16].
Рецензенты:
Живаго Э.Я., д.т.н., профессор, зав. кафедрой «теоретическая механика», ФГОБУ ВПО «Сибирский государственный индустриальный университет», г. Новокузнецк;
Никитин А.Г., д.т.н., профессор, зав. кафедрой «Сопротивления материалов и строительной механики», ФГОБУ ВПО «Сибирский государственный индустриальный университет», г. Новокузнецк.
Работа поступила в редакцию 06.11.2013.



