В работе проводится идентификация процесса синтеза этаноламинов как объекта управления методом регрессионного анализа в условиях мультиколлинеарности статистической выборки [1, 2].
Исследуемый технологический процесс реализован в реакторах непрерывного действия и представляет собой многомерный объект с внутренним и внешним рециклами для проведения сложных последовательно-параллельных реакций.
Системный анализ процесса синтеза как объекта управления с большим числом одновременно и совокупно действующих факторов выполнен с помощью статистических методов.
Целевыми продуктами производства являются моноэтаноламин (МЭА), диэтаноламин (ДЭА) и триэтаноламин (ТЭА) – продукты взаимодействия окиси этилена с аммиаком. Это выходные параметры объекта управления:
– У1 – доля МЭА в реакционной смеси на выходе из узла синтеза ( %);
– У2 – доля ДЭА ( %) в реакционной смеси;
– Уз – доля ТЭА ( %) в реакционной смеси.
В качестве входных, постоянно контролируемых в ходе процесса факторов, приняты следующие:
– X1 – расход окиси этилена (ОЭ), (м /ч);
– Х2 – расход NH3 (м3/ч);
– Х3 – расход МЭА (м3/ч);
– Х4 – подача пара в узел синтеза (м/ч);
– Х5 – температура в верхней части реактора синтеза (°С);
– Х6 – температура в нижней части реактора синтеза (°С);
– Х7 – температура в смесителе (°С);
– Х8 – давление в смесителе (кг/см2).
Блок-схему объекта управления можно представить в виде (рис. 1)
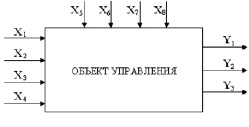
Рис. 1. Принципиальная схема процесса синтеза этаноламинов
Если объединить целевые (выходные) переменные узла синтеза, вектор Y(Y1, Y2, Y3), входные параметры управления узла синтеза, вектор U(X1, Х2, Х3, Х4), параметры состояния реактора, вектор ХP(Х5, Х6) и параметры состояния смесителя, вектор ХС(Х7, Х8), то получится обобщённая схема управления (рис. 2).
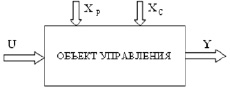
Рис. 2. Обобщённая принципиальная схема процесса синтеза этаноламинов
Для изучения статических характеристик объекта управления использовали метод пассивного контроля квазистатики узла синтеза. Исходная статистическая выборка включала 170 результатов наблюдений. В процессе сбора информации были исключены неполные данные и результаты ошибочных измерений, что позволяет считать выборку репрезентативной (представительной).
На первом этапе исследования объекта выполнили корреляционный анализ связей между параметрами многофакторного процесса синтеза этаноламинов. Коэффициенты парной корреляции, вычисленные для всех пар, включенных в анализ факторов, показаны в таблице.
Матрица коэффициентов парной корреляции
|
Расходы, м3/ч |
Температура, °C |
Давление |
Соотношение, % |
||||||||
|
ОЭ |
NH3 |
МЭА |
Пар |
Рн |
Рв |
См |
См |
МЭА |
ДЭА |
ТЭА |
|
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
Y1 |
Y2 |
Y3 |
|
|
X1 |
1 |
||||||||||
|
X2 |
0,596 |
1 |
|||||||||
|
X3 |
0,645 |
0,556 |
1 |
||||||||
|
X4 |
0,552 |
0,161 |
0,352 |
1 |
|||||||
|
X5 |
0,557 |
0,381 |
0,31 |
0,247 |
1 |
||||||
|
X6 |
0,524 |
0,281 |
0,153 |
–0,20 |
0,952 |
1 |
|||||
|
X7 |
0,373 |
0,388 |
0,645 |
0,282 |
0,227 |
0,125 |
1 |
||||
|
X8 |
–0,03 |
0,146 |
0,363 |
0,024 |
–0,07 |
–0,16 |
0,611 |
1 |
|||
|
Y1 |
–0,61 |
–0,22 |
–0,25 |
–0,39 |
–0,38 |
–0,44 |
–0,22 |
0,228 |
1 |
||
|
Y2 |
0,341 |
0,087 |
–0,051 |
0,176 |
0,151 |
0,249 |
–0,19 |
–0,15 |
–0,38 |
1 |
|
|
Y3 |
0,594 |
0,227 |
–0,125 |
0,401 |
0,400 |
0,423 |
0,335 |
–0,19 |
–0,92 |
0,157 |
1 |
О наличии или отсутствии линейной или близкой к линейной связи между переменными можно судить по величине коэффициента корреляции. Для проверки гипотезы о существовании линейной или приближающейся к линейной связи использовали критерий Меритерии (Стьюдента) (1):
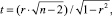 (1)
(1)
где r – выборочный коэффициент корреляции; n – размер выборки.
Если вычисленное значение t для выборочного коэффициента корреляции выше критического значения t-критерия, найденного при заданной доверительной вероятности с имеющимся числом степеней свободы, то связь между исследуемыми факторами можно считать с данной доверительной вероятностью приближающейся к линейной.
В таблице статистически значимые данные с доверительной вероятность не менее р = 0,95 отмечены жирным шрифтом.
Рассмотрение таблицы коэффициентов корреляции показывает, что:
– доля МЭА в продукте зависит в основном от подачи ОЭ и снижается с увеличением подачи ОЭ, а также от температуры в реакторе синтеза, от подачи пара в узел синтеза и в меньшей степени от подачи аммиака и МЭА [4];
– доля ДЭА зависит также от подачи ОЭ (увеличивается с повышением подачи ОЭ), от температуры в реакторе синтеза и в меньшей степени от температуры в смесителе;
– доля ТЭА зависит в первую очередь от подачи ОЭ и растет с увеличением подачи ОЭ, затем от температуры в реакторе синтеза и в смесителе (увеличивается с ростом температуры) и от подачи пара в узел синтеза.
Видно, что основными каналами управления составом реакционной смеси на выходе из узла синтеза являются подача ОЭ, температура в верхней и нижней части реактора синтеза и в смесителе [3, 5].
Корреляционный анализ обнаружил наличие статистически значимых связей между входными факторами или мультиколлинеарность исследуемой статистической выборки. Наличие мультиколлинеарности не позволяет применять для идентификации объекта классический множественный регрессионный анализ. Для устранения или уменьшения влияния мультиколлинеарности статистики использована процедура последовательного (пошагового) регрессионного анализа «от простого к сложному». На первом шаге были получены уравнения парной регрессии для всех выходных переменных от тех факторов, с которыми они были коррелированны. Затем полученные парные уравнения регрессии, которым соответствуют наибольшие коэффициенты корреляции, дополнялись факторами, имеющими меньшие, но статистически значимые коэффициенты корреляции. На каждом шаге выполнялся полный статистический анализ коэффициентов и уравнения регрессии с использованием статистических программ-функций, реализованных в Microsoft Excel. Процедура завершается, когда последующее дополнение моделей факторами не улучшает или даже ухудшает качество регрессии.
Качество регрессии оценивали, анализируя ошибки в определении коэффициентов регрессии и показатели адекватности модели: коэффициент детерминации (D), значение критерия Фишера (F) и ошибку регрессии (S). Коэффициент детерминации представляет собой отношение дисперсии, обусловленной регрессией, к общей дисперсии выборки и характеризует «прогностическую» силу уравнения регрессии. Критерий Фишера характеризует адекватность модели: гипотеза о соответствии модели результатам наблюдений считается не противоречащей эксперименту, если с данной доверительной вероятностью и имеющимся числом степеней свободы вычисленное значение критерия превышает его критическое (табличное) значение.
Как уже отмечалось ранее, на состав реакционной смеси, выходящей из узла синтеза, наиболее активно влияет подача ОЭ, поэтому за основные парные регрессионные уравнения на первом шаге анализа приняли уравнения связи долей МЭА, ДЭА и ТЭА с подачей ОЭ. Для оценки связи доли МЭА с подачей ОЭ используется уравнение (2):
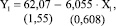 (2)
(2)
В скобках здесь и далее указаны ошибки в оценке соответствующих коэффициентов регрессии.
Значения D = 0,371, F = 99,02, S = 3,32. Уравнение адекватно с доверительной вероятностью выше р = 0,95. Более 37 % общей дисперсии выборки объясняется регрессией и ошибка регрессии ±3,32. Уравнение парной регрессии было дополнено следующим по силе связи входным параметром-температурой вверху реактора синтеза (Х5) (3):
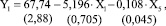 (3)
(3)
Значения D = 0,391, F = 53,5, S = 3,28, что показывает некоторое улучшение модели. Критерий Фишера несколько снижается, но его значение остается значительно выше критического.
Следующий шаг (4):
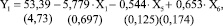 (4)
(4)
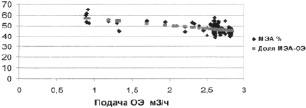
Рис. 3. Доля МЭА в продукте перед разделением в зависимости от подачи ОЭ
Дополнение следующим по величине коэффициента коррекции фактором – Х6 (температура внизу реактора синтеза) дает улучшения модели D = 0,438, F = 43,2, S = 3,151 по статистическим показателям. Однако направление влияния фактора Х6 сменилось на противоположное, вследствие высокой коррелированности факторов Х5 и Х6, r(Х5, Х6) = 0,952 произошло смешение эффектов факторов. В модель следует включать только один из них.
На следующем шаге в модель включен фактор Х4 – подача пара в узел синтеза (5)
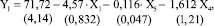 (5)
(5)
Показатели статистики: D = 0,397, F = 36,2, S = 3,27. Значительно снизилась величина критерия Фишера и вследствие значимой корреляции факторов Х5 и Х4, r = 0,25 резко возросла ошибка в оценке эффекта фактора Х4. Следовательно Х4 не целесообразно включать в регрессионную модель.
На следующем шаге в модель включили два фактора X2 и Х3, имеющие почти одинаковые коэффициенты корреляции с Y1 (6).
 (6)
(6)
Статистика: D = 0,444, F = 32,9, S = 3,151, показывает некоторое улучшение показателей адекватности модели при заметном росте ошибок в оценке коэффициентов регрессии.
Предпочтительной для целей управления является модель:
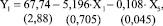
Уравнение регрессии для содержания ДМ в реакционной смеси в зависимости от подачи ОЭ имеет вид (7):
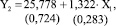 (7)
(7)
Показатели адекватности модели D = 0,115, F = 22,05, S = 1,548 свидетельствуют о ее невысокой прогностической силе. Дополнение модели другими коррелированными эффектами приводит к росту ошибок в оценке коэффициентов регрессии.
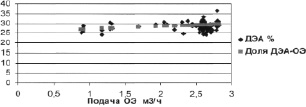
Рис. 4. Доля ДЭА в продукте перед разделением в зависимости от подачи ОЭ
Уравнение регрессии для зависимости доли ТЭА в продукте синтеза от подачи ОЭ (8):
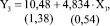 (8)
(8)
Показатели статистического анализа: D = 0.323, F = 80.23, S = 2.945.
Включение в модель дополнительных факторов приводит к увеличению коэффициента детерминации, но при этом к росту ошибок в оценке коэффициентов регрессии. Наиболее приемлемой для целей управления является вышеприведенная модель, а также несколько расширенная модель (8):
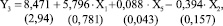 (9)
(9)
с показателями адекватности; D = 0б393, F = 35б9, S = 3б033. Полученные выше регрессионные модели пригодны для целей прогнозирования состава продукта синтеза и для управления составом в зависимости от спроса.
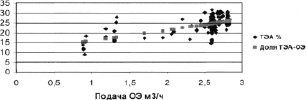
Рис. 5. Доля ТЭА в продукте перед разделением в зависимости от подачи ОЭ
Рецензенты:
Луконин В.П., д.т.н., профессор, генеральный директор ФГУП «НИИ полимеров им. академика В.А. Каргина», г. Дзержинск;
Никандров И.С., д.т.н., профессор кафедры «Автомобильный транспорт и механика» Дзержинского политехнического института (филиал) ФГБОУ ВПО Нижегородский государственный технический университет им. Р.Е. Алексеева, г. Дзержинск.
Работа поступила в редакцию 06.11.2013.



