В современной алгоритмической теории большие и сверхбольшие числа играют важную роль в криптографии для построения шифров различной сложности и для тестирования производительности суперкомпьютеров [4, 8]. Исследование сверхбольших чисел [5] показало, что они имеют величины, которые трудно или почти невозможно поразрядно представить в обычных позиционных системах счисления.
Если число A = 22147483647 возвести в указанную степень, то оно будет иметь более миллиона разрядов. Поэтому такие числа нецелесообразно представлять в обобщенной позиционной системе счисления в натуральном исходном состоянии.
Представим сверхбольшие многоразрядные числа с помощью обычной позиционной системы счисления, в виде информационной системы, показанной на схеме вычисления сверхбольших чисел (рис. 1), и проанализируем их.
На схеме показано, что на вход алгоритма вычисления сверхбольших чисел (стрелки слева) поступают сверхбольшие многоразрядные числа, стрелки «сверху-вниз» обозначают позиционную систему счисления и арифметические операции. На выходе алгоритма сверхбольшое число-результат. Однако если число-результат отобразить в обычной позиционной системе, то возникают проблемы:
- Число не вмещается в типовой компьютерный диапазон [0, ..., 231].
- Временные затраты на представление числа в обобщенной позиционной системе.
- Нагрузка на объем оперативной памяти, если число состоит из связанных списков.
По схеме абстрактного представления сверхбольшого многоразрядного числа (рис. 2) на выходе получается сверхбольшое число, которое не вмещается в типовой компьютерный диапазон. Наглядно выполнять какие-либо операции с таким числом не представляется возможным, так как оно занимает сотни страниц файлов любого типа из операционной системы Windows.
В связи с этим сверхбольшие многоразрядные числа A = 22147483648 эффективно представлять в непозиционной системе счисления – системе остаточных классов, где нет переносов из младших разрядов в старшие.
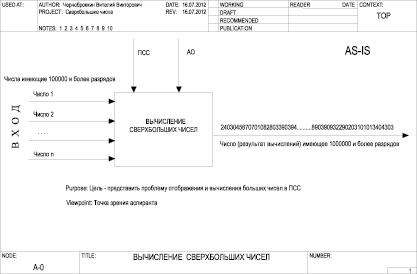
Рис. 1. Схема вычисления сверхбольших чисел
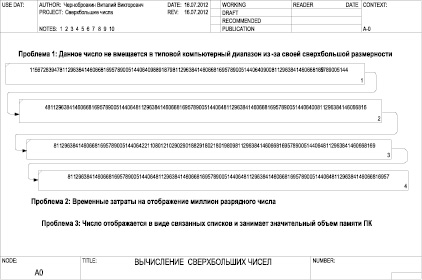
Рис. 2. Схема абстрактного представления сверхбольшого многоразрядного числа в виде связанных списков
Существует проблема, которая состоит в следующем: если сверхбольшое многоразрядное число представить с помощью системы остаточных классов [5, 7], то число остатков, как и выбранная система оснований, будет большим, что в свою очередь влияет на вычислительные процессы.
Введем числовой диапазон в двоичной позиционной системе [265537, ..., 22147483648].
Утверждение 1 Число A = 22147483648, имеющее количество разрядов из диапазона [265537, ..., 22147483648] и более, можно называть сверхбольшим многоразрядным числом.
Число, имеющее миллион и более разрядов, можно назвать сверхбольшим многоразрядным, так как в реальном исполнении оно имеет большое численное значение.
Утверждение 2 Сверхбольшие многоразрядные числа, представленные в системе остаточных классов, зависят от веса позиционного ранга |Z|P [1], а значит, могут состоять из большого множества выбранных модулей и соответственно остатков. Вес позиционного ранга |Z|P зависит от содержания в нем количества простых чисел. При вычислении сверхбольших чисел в системе остаточных классов нужно учитывать следующее равенство:
0 ≤ A ≤ P, (1)
где A – число, результат вычисления;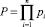 
– основания модулярной системы, взаимно простые числа.
Утверждение 3 Сверхбольшое число можно представить с помощью системы остаточных классов в виде остатков от вычетов [3, 5, 6, 7]
a ≡ b(mod p). (2)
Возможность такого представления числа определяется следующими теоремами.
Теорема 1 (Китайская теорема об остатках) [2, 3, 5, 6, 7].
Любое целое положительное число в системе остаточных классов можно представить в виде набора остатков (вычетов) от деления этого числа на выбранные основания (модули) системы.
Доказательство: Пусть число А = 22147483648 представлено в системе остаточных классов как
A(a1, a2, ..., an), (3)
где a1, a2,…, an – наименьшие неотрицательные остатков (вычетов), образованные путем целочисленного деления числа A на выбранные основания
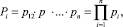(4)
где pi – взаимно простые числа.
Пример:
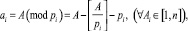(5)
И если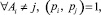 
то представление числа (3) является единственным при условии
0 ≤ A ≤ Pi. (6)
Тогда число A будет выглядеть следующим образом:
A ≡ a1(mod p1);
A ≡ a2(mod p2); (7)
. . . . . . . . . .
A ≡ an(mod pn).
Теорема доказана.
Докажем п. 1.6.
Теорема 2 Если числа в pi = p1, p2, ..., pn попарно взаимно просты, то для любых остатков a1, a2, ..., an, таких, что 0 ≤ an ≤ pn при всех i = 1, 2, ..., n найдется число A, которое при делении на pi дает остаток ai при всех i = 1, 2, ..., n
Доказательство: Применим индукцию по. При n = 1 утверждение теоремы очевидно. Пусть теорема справедлива при n = k – 1, т.е. существует число M, дающее остаток ri при делении нa pi при i ∈ {1, 2, ..., k – 1}. Обозначим
d = a1, a2, ..., ak–1. (8)
Рассмотрим числа M, M + d, M + 2d, ..., M(ak – 1)d. Покажем, что хотя бы одно из этих чисел даёт остаток rk при делении на ak. Предположим, что это не так. Поскольку количество чисел равно ak, а возможных остатков при делении этих чисел на ak может быть не более чем ak – 1 (т.к. ни одно число не даёт остаток rk), то среди них найдутся два числа, имеющих равные остатки. Пусть это числа
M + sdи M + tdM при 0 ≤ s ≤ ak
и 0 ≤ t ≤ ak и s ≠ t. (9)
Тогда их разность
(M + sd) – (M + td) = (s – t)d
делится на ak, что невозможно, т.к. 0 < s – t < ak и d = a1, a2, ..., ak–1 взаимно просто с ak, ибо числа a1, a2, ..., ak–1 попарно взаимно просты (по условию). Противоречие.
Теорема доказана.
Так как речь идет о миллион разрядных числах, то опишем реальные проблемы их построения в системе остаточных классов:
- Выбор количества оснований
- Разрядность выбранных оснований
- Многоразрядность остатков
Это означает, что, если мы строим сверхбольшие числа, у которых миллион и более разрядов, то количество оснований системы будет зависеть от разрядности этих чисел. Так, например, если разрядность каждого из выбранных оснований маленькая, то соответственно количество оснований нужно увеличивать. И, наоборот, если разрядность выбранных оснований большая, то их нужно уменьшить до необходимого количества. То есть речь идет о расширении или сужении оснований системы остаточных классов [7]. Еще одна проблема состоит в том, что при отображении сверхбольшого числа A = 22147483648 в системе остаточных классов остатки могут быть тоже многоразрядными.
В общем случае решить вышеперечисленные проблемы можно с помощью Малой теоремы Ферма, доказательство которой приведено в [2, 6] и Китайской теоремы об остатках [2, 3, 5, 6, 7].
Основной смысл Малой теоремы Ферма состоит в том, что если p – положительное простое число, a – целое, тогда
ap–1 ≡ 1(mod p), если p – простое число, (10)
значит, аk ≡ ar(mod p) и достаточно делать вычисления только для экспонент, показатель которых меньше р – 1.
Применяя Китайскую теорему об остатках, можно упростить отображение сверхбольших чисел. Показав их в виде вычетов степеней по модулю n, если известно его разложение на простые множители. Предположим, что каждый простой множитель входит в это разложение с кратностью 1, потому что именно в таком случае метод наиболее эффективен.
Допустим, что разложение имеет вид
n = p1 ... pk, (11)
где 0 < p1 < ...pk – простые числа.
Для целых чисел а и m сначала находим вычет аm по каждому модулю pi. Если простые множители не слишком велики, то вычисления будут очень быстрыми даже для больших m и a, поскольку нам помогает это делать Малая теорема Ферма (п. 10).
Предположим, что вычисления сделаны, причем
am ≡ r1(mod p1) и 0 ≤ r1 ≤ p1;
am ≡ r2(mod p2) и 0 ≤ r2 ≤ p2; (12)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
am ≡ rk(mod pk) и 0 ≤ rk ≤ pk.
Поэтому для определения вычета am по модулю n нужно решить систему сравнений:
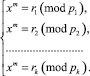(13)
Напомним, что модули системы – различные попарно взаимно простые числа. Значит, по Китайской теореме об остатках система всегда имеет решение, к примеру r, 0 ≤ ri ≤ pi – 1. Более того, любые два таких решения сравнимы по модулю p1 ... pk = n … . Так как am тоже решение системы, имеем am ≡ r(mod n). Следовательно, r – вычет amпо модулю n.
Пример. Сюръективно отобразим число A = 22147483648 в виде вычетов по выбранным основаниям p1 = 11, p2 = 13, p3 = 17, p4 = 19. Изменив при этом степень указанного числа на единицу 2147483648 – 1 = 2147483647, применим Малую теорему Ферма, для чего найдем остатки от деления степени 2147483647 (на p – 1) каждого выбранного основания p1, p2, p3, p4. Тогда
pi–1 = 11 – 1 = 10; pi–2 = 13 – 1 = 12;
pi–3 = 17 – 1 = 16; pi–4 = 19 – 1 = 18; (14)
a′1 = 2147483647 mod 10 = 7;
a′2 = 2147483647 mod 12 = 7; (15)
a′3 = 2147483647 mod 16 = 15;
a′4 = 2147483647 mod 18 = 1.
Следовательно
a1 = 22147483647 ≡ 27(mod 11);
a2 = 22147483647 ≡ 27(mod 13); (16)
a3 = 22147483647 ≡ 215(mod 17);
a4 = 22147483647 ≡ 21(mod 19).
Окончательно число A = 22147483647 будет выглядеть:
27 ≡ 7(mod 11);
27 ≡ 11(mod 13); (17)
215 ≡ 9(mod 17);
2 ≡ 2(mod 19).
Выводы
1. Распараллеливание представлений сверхбольших многоразрядных чисел с помощью системы остаточных классов дает преимущество по времени для вычислений при большом объеме обрабатываемых данных, так как вся обработка информации происходит параллельно и независимо друг от друга.
2. Любое многоразрядное число можно представить в виде остатков от степенных вычетов.
3. Над представленными параллельным образом числами можно проводить ускоренные параллельные вычисления.
4. Если образование остатков ai, производится независимо друг от друга, то каждое вычисление будет также происходить не зависимо друг от друга.
Рецензенты:
Инютин С.А., д.т.н., профессор кафедры «Проектирование вычислительных комплексов», ФГБОУ ВПО «Российский государственный технологический университет им. К.Э. Циолковского (МАТИ)», г. Москва;
Бахарев М.С., д.т.н., профессор кафедры «Нефтегазовое дело», ФГБОУ ВПО «Сургутский институт нефти и газа, филиал Тюменского государственного нефтегазового университета», г. Сургут;
Криштоп В.В., д.ф.-м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Университета Kwangwoon University, Korea.
Работа поступила в редакцию 19.12.2013.