Необходимость и актуальность стратегического планирования развития регионального туризма в Новгородской области является следствием маркетингового исследования туристической отрасли и возникших в ней проблем. Само исследование целесообразно проводить с помощью системного анализа, а разрешение последних – с помощью применения математических методов, так как они позволяют четко регламентировать процесс выявления и решения проблем при соблюдении соответствующей последовательности этапов.
Наиболее важными и сложными этапами в этой последовательности являются:
– определение цели решения проблем и принуждающих связей;
– определение критерия – показателя, оценивающего степень достижения цели и позволяющего сравнивать альтернативы решения проблемы;
– определение исследуемой системы управляемых переменных;
– построение набора альтернатив, представляющих собой объединение некоторых управляемых переменных, дающее существенное приращения критерия;
– выбор наилучшей альтернативы по наибольшему (наименьшему) значению критерия.
Эта последовательность этапов связана с процессами определения стратегических целей развития туризма в регионе и моделирования, комплекс которых является частью программно-целевого регулирования экономики региона.
Отличительной особенностью построения математической модели развития регионального туризма является ее большая размерность. В частности, при решении задач оптимального планирования на макроуровне матрица ограничений достигает размерности более 102. При такой размерности классические методы математического программирования (линейного, нелинейного, дискретного) оказываются малоэффективными [1].
В связи с этим возникла необходимость разработки специальных методов большей частью приближенных, предназначенных для задач большой размерности. Большинство из этих методов использует теорию декомпозиции, которая заключается в расчленении исходной задачи большой размерности, нахождении независимых решений для каждой из них и последующей увязке этих частных решений в общее решение исходной задачи. Впервые идея декомпозиции применительно к задачам линейного программирования была сформулирована Данцигом и Вульфом [4], а позднее была развита в работах [3, 5] и др.
В результате применения метода декомпозиции [2] можно смоделировать стратегию развития регионального туризма, представляющую собой так называемое «дерево целей». Метод «дерева целей» позволяет охватить достаточно существенное число возможных мероприятий, которые можно использовать для решения проблемы, но не обеспечивает их количественное сравнение.
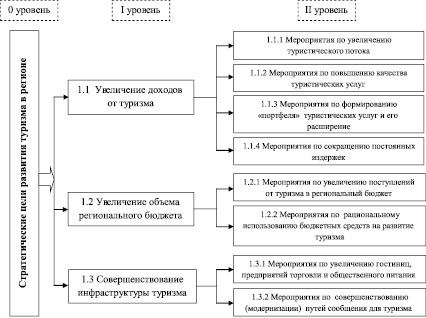
Декомпозиционная модель стратегического развития туризма в регионе
Для того чтобы обеспечить это количественное сравнение, для каждой подцели «дерева» надо сопоставить критерий и получить функциональную зависимость его от такого комплекса управляемых переменных, изменение которых было бы адекватно изменению комбинаций определенной группы мероприятий. Если это удается, то возможно построение математической модели для оценки движения к рассматриваемой подцели. Если же это удается сделать для каждой подцели «дерева», то возникает комплекс микромоделей, из которого можно выбрать модель для решения рассматриваемой проблемы. Построение такой модели – это завершающая процедура целевого анализа.
Для реализации этой процедуры лучше всего применить конструкцию под названием «дерево целевых задач». Построение такого «дерева» идет параллельно построению «дерева целей». Каждой цели «дерева целей» ставится в соответствие своя целевая задача под номером соответствующей цели (на рисунке – это задачи II уровня).
Рассмотрим формирование целевой задачи, входящей в состав стратегии развития регионального туризма, которая выбрана при возникновении проблемной ситуации, в которую попал регион, не выдержавший конкуренции в своем сегменте туристского рынка, в результате чего у него упал туристский поток, снизились доходы и прибыль от туризма (задача 1.1 – I уровень).
Эта целевая задача представляет собой задачу оптимизации, когда по выбранному критерию может достигаться его максимум или минимум.
В рассматриваемой ситуации критерий совпадает с целью, которая представляет собой годовой туристский поток и полученную прибыль от реализации товаров и услуг, и эту прибыль следует максимизировать за счет изменения некоторых управляемых переменных, от которых прибыль должна зависеть.
Функциональная зависимость прибыли от управляемых переменных и тип самих переменных должны определяться основными соотношениями между экономическими показателями, характеризующими функционирование туризма в регионе. В данном случае можно использовать основное соотношение между прибылью, выручкой, количеством продаваемых туристам товаров и услуг и всеми видами затрат.
Тогда математическая формулировка целевой задачи будет иметь следующий вид:
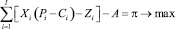 (1)
(1)
при следующих ограничениях
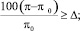 (2)
(2)
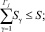 (3)
(3)
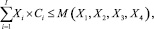 (4)
(4)
где π – максимизируемая прибыль туристической отрасли региона; π0 – минимальная годовая прибыль туристической отрасли региона в результате возникновения проблемной ситуации; Xi – управляемые переменные – число проданных единиц i-го товара (услуги) за год; I – число типов продаваемого товара (услуги); Pi – продажная цена i-го товара (услуги); Сi – производственные затраты на единицу i-го товара (услуги); Zi – годовые маркетинговые затраты на продажу i-го товара и услуги туристского ассортимента; А – постоянные издержки предприятий и организаций, обслуживающих туристов; Δ – минимальное потребное приращение прибыли в процентах; Sγ – затраты на γ-е мероприятие по преобразованию предприятий и организаций туристической отрасли региона, входящих в рассматриваемую альтернативу; Γj – число мероприятий, входящих в j-ю альтернативу; S – финансовые возможности предприятий и организаций регионального туризма; М(X1, X2, X3, X4) – потенциальные возможности региона по реализации товаров и услуг туристского назначения в стоимостном выражении как функция изменений X1 туристского потока, изменений X2 технологии обслуживания туристов (повышение качества), X3 производственной структуры, изменений X4 структуры аппарата управления.
Неравенства (2)–(4) представляют собой принуждающие связи, вводящие проблему в определенные границы.
Так, условие (2) является ограничением прибыли снизу, т.е. приращение прибыли должно быть больше Δ.
Условие (3) является ограничением прибыли по суммарной стоимости мероприятий, направленных на ее увеличение.
Условие (4) сдерживает рост производимых товаров и услуг туристского назначения, а значит, и прибыли за счет недостаточных производительности труда, уровня организации управления, темпов модернизации предприятий туриндустрии.
В сформированной задаче оптимизации все величины, кроме π и Xi, являются параметрами и для начальной стадии построения дерева целей и дерева целевых задач должны быть заданы как исходная информация. Это позволяет перед началом декомпозиции главной выбранной цели попытаться решить задачу оптимизации и получить оптимальный план реализации товаров и услуг туристского назначения {Xi} и соответствующую ему максимальную прибыль π, если условия (2)–(4) будут выполнены.
Если эта попытка удастся, то проблема неконкурентоспособности регионального турпродукта решается только за счет оптимизации плана реализации товаров и услуг туристского назначения, и строить дерево целей и дерево целевых задач не нужно.
Если же при решении задачи оптимизации хотя бы одно из указанных условий не выполняется, то проводится первый шаг декомпозиции главной цели.
Путь декомпозиции определяется видом целевой функции (1) и условий (2)–(4). Из целевой функции (1) следует, что для увеличения прибыли необходимо совместно или порознь проводить следующие действия:
– увеличивать выручку Bi = Pi×Xi;
– увеличивать число типов реализуемых туристам товаров и услуг I;
– сокращать производственные затраты Ci;
– сокращать маркетинговые затраты Zi;
– сокращать постоянные издержки А.
Из условия (3) следует, что для расширения множества мероприятий, используемых для различных изменений параметров, возможно, будет необходимо увеличивать финансовые возможности региона S.
Из условия (4), если сделать подстановку, следует, что при увеличении выручки Bi, начиная с некоторых их значений, реальной мощности предприятий туриндустрии может не хватить, и потребуется ее увеличение, сбалансированное с другими условиями.
Рассмотренный путь декомпозиции реализован в целях I уровня, далее для каждой цели I уровня должна быть сформирована своя целевая задача оптимизации II уровня.
Если все условия целевой задачи выполняются, то проблема решена.
В противном случае начинается второй шаг декомпозиции, на котором выявляются подцели III уровня. Процесс декомпозиции заканчивается тогда, когда ни в одной ветви дерева целей новая подцель не выявится.
Заключение
Предлагаемая математическая модель стратегического развития регионального туристского рынка, в основу которой положен метод декомпозиции целей стратегического развития туризма в регионе, в общем случае относится к задачам с нечеткими условиями, так как велико влияние факторов неопределенности и случайности.
Комплексный подход к стратегическому планированию и прогнозированию развития туризма в регионе является актуальным. В рамках этого подхода в качестве одной из его составляющих предлагается авторский алгоритм стратегии развития туризма в регионе, который позволяет прогнозировать такие показатели, как уровень развития туризма в регионе, величину и структуру туристского потока, величину доходов.
Рецензенты:
Бондаренко Е.А., д.т.н., профессор, проректор по научной работе НовГУ им. Ярослава Мудрого, г. В. Новгород;
Омаров М.М., д.э.н., профессор, декан факультета управления ИЭУ, НовГУ им. Ярослава Мудрого, г. В. Новгород.
Работа поступила в редакцию 04.04.2014.



