Для разработки данной темы явилась причина разрушения отдельных высотных сооружений, построенных в регионах Южного Казахстана. Безусловно, такие разрушения зданий явились последствием неправильного расчета грунтовых оснований, и в основном это связано с тем, что здесь неполноценно учитывались вопросы консолидации, ползучести и свойства старения грунта.
Решение проблемы прочности и надежности возводимых сооружений при строительстве гидротехнических, крупнопромышленных, транспортных и гражданских сооружений базируется на вопросах консолидации грунтового основания с учетом его многофазной структуры. Вопросы определения конечных осадок в теории механики уплотняемых многофазных грунтов, а также учет реологических и свойства старения грунтовых оснований представляет большой интерес при строительстве любого сооружения.
Успех инженерного прогнозирования подобных процессов, протекающих в массиве глинистого грунта под действием поверхностных и объемных сил, во многом зависит от того, с какой степенью точности и полноты отражены свойства грунта и характер взаимодействия фаз и частиц в математической модели, выбранной для описания его напряженно-деформированного состояния.
В данной работе в качестве такой модели выбрана общая модель В.А. Флорина [7]. При этом упругоползучее свойство уплотняемого грунта описывается теорией Г.Н. Маслова – Н.Х. Арутюняна [6]. Согласно этой теории зависимость между коэффициентом пористости грунта и суммой главных напряжений в представлении В.А. Флорина имеет вид:
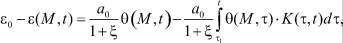(1)
где e0 - начальный коэффициент пористости; x - коэффициент бокового давления; e(М,t) - коэффициент пористости для исследуемого момента времени t; a0 - коэффициент сжимаемости уплотняемого грунта; θ(M, t) - сумма главных напряжений.
Подынтегральная функция K(τ, t), входящая в соотношение (1), согласно Н.Х. Арутюняну [1] запишется в виде
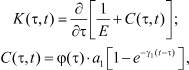(2)
где φ – функция старения, зависящая от физико-механических свойств уплотняемого грунта; a1, γ1 – параметры ползучести; E – модуль общей деформации уплотняемого грунта.
Если давление в поровой жидкости не зависит от угла q, то основное уравнение, отражающее неразрывность твердой и жидкой фаз грунта согласно [5] относительно цилиндрических координат представляется так:
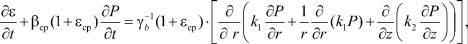(3)
где β1 – коэффициент объемного сжатия; εср – средний коэффициент пористости; Р(М, t) – давление в поровой жидкости; γb – объемный вес воды; k1, k2 – коэффициенты фильтрации во взаимно-перпендикулярных направлениях.
Условие равновесия нестабилизированного состояния уплотняемого грунтового массива согласно основной модели В.А. Флорина имеет вид
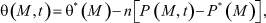(4)
где θ*, P* – сумма главных напряжений и давление в поровой жидкости для стабилизированного состояния уплотняемого грунтового массива; x, y, z – координаты точки M.
Рассматривая совместно выражения (1)–(4), в безразмерных координатах получим уравнения вида
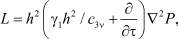(5)
с начальными условиями
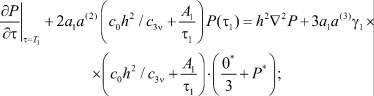(6)
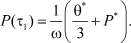(7)
Здесь L – дифференциальный оператор вида
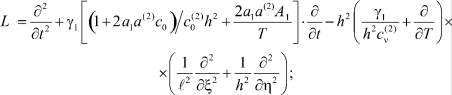(8)
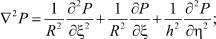(9)
ξ, η - безразмерные координаты; с0 - предельное значение меры ползучести для уплотняемого грунта; А1 - параметр, зависящий от свойств и условий старения грунта; a0, βср, ξ, k, γb, εср - параметры грунта.
Далее решим систему уравнений (5)–(8) применительно к ограниченной области уплотнения. Вначале решим для уплотнения слоя грунта в виде цилиндра радиуса R высотой h с водопроницаемым дном и стенками под действием равномерно распределенной нагрузки с интенсивностью q, приложенной на части площади верхней поверхности с радиусом a < R. Уплотненный многофазный грунт считается упругоползучей стареющей средой. Применительно к этой схеме требуется определить непрерывную функцию Р в области (G = (0 < r < R; 0 < x3 < h; t > 0), удовлетворяющую дифференциальному уравнению вида (5) и граничным условиям
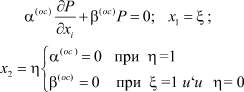. (10)
Здесь
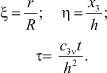(11)
Решение данной краевой задачи (5)–(10) при (11) дает возможность определить давление в поровой жидкости для любого момента времени относительно безразмерных координат.
Начальное распределение порового давления для рассматриваемой задачи относительно безразмерных координат представляется в виде
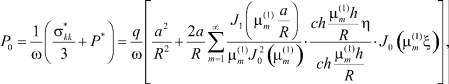(12)
где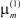 
– является бесчисленным множеством положительных корней трансцендентного уравнения
J1(μ) = 0; (13)
J0(x) и J1(x) – функции Бесселя первого рода соответственно нулевого и первого порядка.
Здесь необходимо заметить, когда h = 1 сумма ряда, полученная из (12) при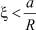 
равна q, а при 
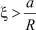– нулю, соответствует краевым значениям исследуемой задачи для начального момента времени.
Решение краевой задачи (5)–(10) представим в виде
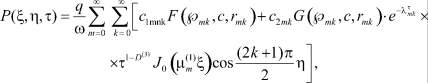(14)
где
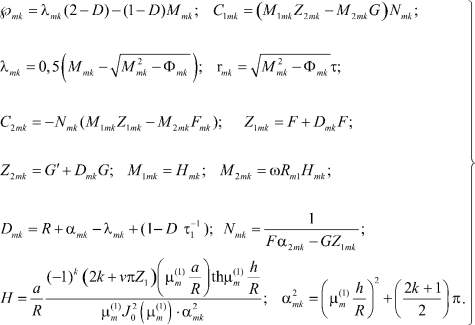(15)
Выражение (14) при (15) действительно является решением уравнения (5), удовлетворяющим граничным условиям (10). В этом можно легко убедиться непосредственной подставкой (14) в (5)–(10).
Сумму главных напряжений в грунтовом цилиндре можно вычислить по формуле
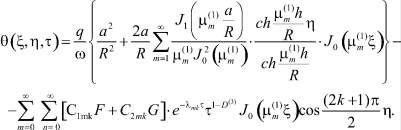(16)
После определения суммы главных напряжений осадку уплотняемого слоя грунта можно вычислить по формуле
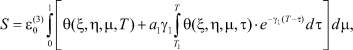(17)
где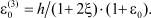 
Выражение (16), подставив в (17) осадку слоя грунта, представим в виде
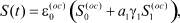(18)
где
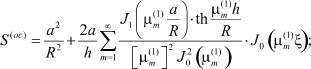
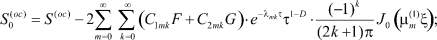
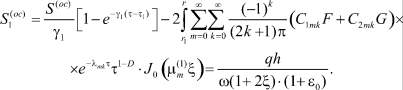
Таким образом, выражениями (14) и (17) будут вычислены поровое давление и вертикальные перемещения точек верхней поверхности уплотняемого массива. Они в основном зависят от параметров a0, c0, βср, k, εср, определяемых по результатам компрессионных испытаний грунтов, по величинам начального, конечного и изменяющегося во времени порового давления и осадок.
Аналогичные задачи теории консолидации грунтов исследованы в работах [2–4, 8].
Рецензенты:
Печёрский В.Н., д.т.н., профессор, Южно-Казахстанский государственный университет имени М. Ауэзова, г. Шымкент;
Бровко И.С., д.т.н., профессор, Южно-Казахстанский государственный университет имени М. Ауэзова, г. Шымкент.
Работа поступила в редакцию 30.04.2014.