Задачи проектирования автоматизированных систем многокритериальны: чем больше критериев качества вводится в рассмотрение, тем более полную характеристику достоинств и недостатков проектируемой системы получает конструктор. Проектирование систем с учетом многих критериев качества обычно имеет характер эвристического итерационного процесса путём мысленного творческого системного анализа и синтеза [6]. Поскольку метод аналитического выражения связи параметров полюсов спектральной функции с показателями качества замкнутой системы, оптимальной по многим критериям и удовлетворяющей поставленным ограничениям, к настоящему времени не разработан, целевая функция задана неявно, система оценивается как количественными, так и качественными критериями, то аналитические методы решения неприменимы.
Формальные обобщенные методы принятия решений, основанные на правилах сравнения вариантов или на сформированных обобщенных целевых функциях, рассматривает абстрактная математическая теория векторной оптимизации [2]. Выбор оптимальной альтернативы в этих методах осуществляется в неитерационном аспекте, ибо принятое правило выбора (или целевая функция) не корректируются по результатам принятого решения [2, 3]. При проектировании автоматизированных систем многокритериальная оптимизация не может решаться целиком формализованным путем [2, 4, 5]. Выбор функционала и механизма принятия решения, их уточнение производятся лицом, принимающим решение, итерационно, то есть с коррекцией по полученным (например, путем моделирования) результатам. Интеллектуальные методы принятия решений характерны тем, что требуют лишь частичной информации о степени предпочтений конструктора, не накладывая строгих ограничений на ее структуру.
Постановка многокритериальной задачи оптимального расположения полюсов спектральной функции на комплексной плоскости автоматической системы
Без ограничения общности конкретизируем постановку задачи оптимального управления объектом третьего порядка, где требуемая спектральная функция замкнутой системы имеет три изменяемых полюса.
1. Формулирование цели исследования (цели управления).
В обобщенной форме цель управления – формирование переходной функции с оптимальными показателями качества путем максимизации функционала качества F(x), выраженного через частные целевые функции качества.
1.1. Технологическая цель (формулирование цели в содержательном аспекте; выражает граничные условия): перейти из одного заданного состояния в другое с предельно возможными быстродействием и точностью.
1.2. Математическая цель (формулирование цели в формальном аспекте; оптимизация параметров полюсов требуемой спектральной функции замкнутой системы путем максимизации функционала качества): найти вектор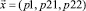 
, при котором формируется такой закон изменения во времени управления u(t) на объект, при котором система при заданных ограничениях перейдет из одного заданного состояния в другое таким образом, что функционал качества F(x) получит при найденном 
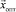наибольшее значение.
Составляющие вектора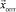 
:
p1 – действительный полюс;
p21 – действительная часть комплексного полюса p2;
p22 – мнимая часть комплексного полюса p2.
2. Формирование множества критериев качества управления:
2.1. Время регулирования (быстрое затухание переходного процесса благотворно влияет на износ механических передач, энергетику привода и производительность установки) tp, c.
2.2. Перерегулирование σ, %.
2.3. Время нарастания переходной характеристики (Rise Time) – tнp, c.
2.4. Максимальное отклонение регулируемой координаты от требуемого значения при действии возмущающих факторов.
Требование минимума по возмущающему воздействию фактически является требованием инвариантности до ε (или ограниченной чувствительности) к вариации внешних возмущений;
2.5. Статическая точность работы системы (Final – установившееся значение выходной функции) – hуст.
2.6. Динамическая точность работы системы:
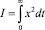– интегральная оценка динамической точности работы системы.
Обобщенный критерий (цель управления, выраженная через функционал качества управления) конструируется эвристически исследователем.
3. Формирование множества альтернатив (множество векторов заданного пространства параметров).
Изменяемые параметры требуемой спектральной функции системы:
3.1. Величина действительного полюса p1;
3.2. Величина действительной части комплексного полюса p21;
3.3. Величина мнимой части комплексного полюса p22.
4. Формирование множества ограничений.
4.1. Функциональные ограничения, представляющие собой системы дифференциальных или разностных уравнений, ограничивающих возможные способы движения системы, выраженные в форме требуемой спектральной характеристики системы.
4.2. Параметрические ограничения: требование положительности параметра p22 и отрицательности p1 и p21; ограничения в форме нестрогих неравенств.
4.3. Критериальные ограничения:
– запас устойчивости по модулю ΔL ≥ 7 дБ;
– запас устойчивости по фазе Δθ ≥ 30°;
– допустимая величина коэффициента усиления на высоких частотах последовательного стабилизирующего устройства Lc(∞), дБ.
4.4. Ограничения, представляющие собой системы алгебраических уравнений или неравенств, выражающих ограниченность ресурсов или иных величин, используемых при управлении. Ограничения выражены в форме нестрогих неравенств.
Метод выбора оптимальных параметров требуемой спектральной функции автоматической системы
Пусть обобщенная цель проектирования автоматизированной системы есть оптимальный перевод системы из одной точки пространства состояний в другую. И хотя для каждого режима технологического процесса можно указать обобщенную главную цель, процессы управления объектами должны удовлетворять множеству требований, выраженных в виде максимума (или минимума) некоторых целевых функций и ограничений. Выразим главную цель исследования в форме максимизируемого функционала (обобщенного критерия оптимальности), аргументами которого выступают целевые функции:
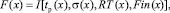
где X – пространство параметров требуемой спектральной функции системы; F(x) – гиперповерхность функционала качества, причем элемент x = (p1, p21, p22); p1 – действительный полюс спектральной функции замкнутой системы; p21 – действительная часть комплексного полюса спектральной функции замкнутой системы; p22 – мнимая часть комплексного полюса спектральной функции замкнутой системы; tp(x) – время затухания переходного процесса, с; σ(x) – перерегулирование, %; RT(x) – (Rise Time) время нарастания переходной характеристики системы; Fin(x) – (Final) установившееся значение переходной характеристики системы.
Lc(∞) – передаточный коэффициент в логарифмическом масштабе последовательного стабилизирующего алгоритма на высоких частотах, дБ.
ΔL – запас устойчивости по модулю, дБ.
Δθ – запас устойчивости по фазе, град.
Предположим, что функционал F(x) имеет первые частные производные. Величины приращений настраиваемых параметров в базовых точках пространства состояний требуемой спектральной функции устанавливаем пропорциональными проекциям градиента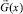 
целевого функционала в пространстве этих параметров:
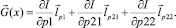
Сформулируем в словесной форме интеллектуальный принцип оптимальности, воплощенный в механизм и алгоритм выбора оптимальной альтернативы:
«Оптимальное движение объекта обладает тем свойством, что каковы бы ни были исходные параметры линейной системы и базовый ансамбль параметров полюсов требуемой спектральной функции замкнутой системы, найдется такой вектор параметров полюсов спектральной функции, при котором функционал качества, сформированный эвристически конструктором на основе выбранного им множества частных целевых функций с установкой рангового приоритета, получит максимальное значение».
Механизм выбора оптимального решения включает следующие элементы: систему критериев, ограничения, функционал качества, градиент качества, структуру предпочтений исследователя, проецируемую на систему критериев, системный анализ, отношение предпочтительности и гипотезы.
Структурная схема алгоритма механизма выбора оптимальной альтернативы приведена на рисунке.
Работает механизм выбора оптимальной альтернативы следующим образом. Пусть проведены модельные эксперименты в базовой точке параметров и ее окрестности и сформирована структура предпочтений исследователя на системе критериев путем классификации критериев на количественные и качественные, упорядочения критериев по важности и установки градационной близости критериев (тем самым формируется многокритериальный виртуальный образ качества работы системы). Затем исследуется функционал качества F(x) в окрестности базового ансамбля параметров сравнением критериев в точках покоординатного приращения параметров с базовыми значениями критериев:
– определяется знак приращения каждого из параметров, при котором качество системы повышается;
– определяется чувствительность критериев к изменению каждого из параметров требуемой спектральной функции;
– оценивается влияние на критерии ограничений оптимизируемых параметров;
– производится упорядочение параметров по чувствительности критериев к заданным величинам приращений параметров;
– выделяются параметры, существенно влияющие на качество работы системы.
Методика анализа качества работы системы по экспериментальным данным следующая.
Пусть известны результаты экспериментов, полученные путем изменения оптимизируемых параметров на некоторую фиксированную величину, например на 10 % от их базовых значений, и проведены структуризация критериев путем их упорядочения по важности, классификация критериев на количественные и качественные, установлена градационная близость критериев. Тогда формы вербального анализа могут быть следующими:
– анализ влияния каждого из оптимизируемых параметров на изменение показателей качества системы;
– экстраполяционный синтез оптимизируемых параметров с целью повышения качества работы системы по каждой целевой функции;
Структурная схема алгоритма работы механизма выбора оптимальной альтернативы
– выводы по результатам исследования: в каком направлении и насколько следует изменять каждый параметр, чтобы улучшить значения наиболее чувствительных к изменению этого параметра и важных показателей качества;
– анализ чувствительности системы к изменениям параметров путем определения частных производных целевых функций по каждому из параметров (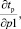
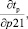
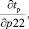
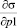и т.д.);
– построение и анализ таблиц данных, где приведены оптимизируемые параметры, оценка их влияния на все критерии и ограничения.
В результате исследования определяется знак приращения по каждому из параметров, то есть определяется ортант расположения градиента качества, затем выбираются величины покоординатных приращений параметров. Далее проводится расчет новых значений параметров полюсов передаточной функции и производятся модельные эксперименты в первой промежуточной точке, результаты которых сравниваются с базовыми. По результатам анализа качества работы системы в первой промежуточной точке определяется направление и осуществляется выбор покоординатных приращений для перехода во вторую промежуточную точку и т.д. до момента фиксирования экстремума.
Рецензенты:
Казанцев В.П., д.т.н., доцент, профессор кафедры «Микропроцессорные средства автоматизации», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Бочкарёв С.В., д.т.н., доцент, профессор кафедры «Микропроцессорные средства автоматизации», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Работа поступила в редакцию 06.11.2014.