Интеллектуальные системы являются одной из наиболее динамично развивающихся отраслей науки и техники. Это обусловлено не только растущими темпами накопления человечеством информации, но и необходимостью эффективно использовать аккумулируемые данные и знания для автоматизированного принятия решений, управления сложными техническими и иными системами, реализации новых видов взаимодействия между человеком и вычислительными устройствами.
Среди интеллектуальных систем наибольшую популярность получили экспертные системы (ЭС), позволяющие хранить, накапливать и использовать экспертные знания с целью автоматизации принятия решений в различных областях. Ядром ЭС является база знаний, включающая механизм принятия решений. Необходимо отметить, что с момента появления первых экспертных систем в семидесятых годах двадцатого века до настоящего времени развитие экспертных систем прошло достаточно большой путь в смысле развития моделей представления знаний: от простейших продукционных моделей с детерминированными правилами вида до комбинации различных способов представления знаний, позволяющих учитывать особенности предметной области.
Представим базу нечетких правил в виде
(V, I, G, P, R), (1)
где V – универсальное множество лингвистических переменных системы; I – множество входных лингвистических переменных, I ⊂ V; G – множество выходных лингвистических переменных, G ⊂ V; P – множество промежуточных лингвистических переменных, P ⊂ V, I ∪ G ∪ P = V, I ∩ G = ∅, I ∩ P = ∅, P ∩ G = ∅; R – множество правил вида
<rj, uj> ЕСЛИ vj,1 есть tj,1 И…И 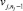 есть
есть 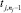 ТО
ТО 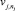 есть
есть 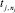 , (2)
, (2)
где rj – уникальное имя правила; uj – лингвистическая степень уверенности в истинности правила rj; nj – количество лингвистических переменных, задействованных в правиле; 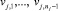 – входные лингвистические переменные для правила rj; их множество обозначим Gj;
– входные лингвистические переменные для правила rj; их множество обозначим Gj; 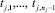 – значения входных лингвистических переменных (термы) для правила rj;
– значения входных лингвистических переменных (термы) для правила rj; 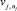 – выходная лингвистическая переменная для правила rj;
– выходная лингвистическая переменная для правила rj; 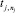 – значение выходной лингвистической переменной для правила rj.
– значение выходной лингвистической переменной для правила rj.
Чаще всего эксперт не может однозначно трактовать те ли иные факты и их влияние на принятие решения. Среди методов, позволяющих обрабатывать неточные знания, часто используется аппарат нечеткой логики, введенный в классических работах Заде [11,12]. Нечеткое множество A может быть представлено в виде
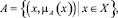 (3)
(3)
где X – универсальное множество; x – элемент множества X; μA(x) – функция принадлежности.
Функция принадлежности μA(x) характеризует степень принадлежности каждого x ∈ X нечеткому множеству A, причем μ:X → [0, 1]. Таким образом, μA(x) принимает значение 1 в случае, если элемент x полностью включен во множество A, и значение 0 в случае, если элемент x не включен во множество A. Значения функции принадлежности, лежащие на интервале (0, 1), характеризуют нечетко включенные элементы.
Общая схема механизма принятия решений в ЭС, основанных на нечетком выводе, представлена на рисунке.
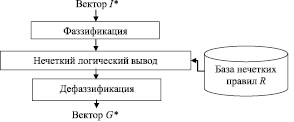
Схема системы нечеткого логического вывода
В литературе описано несколько различных подходов и алгоритмов принятия решений с использованием нечеткого вывода. Стоит отметить, что каждый из описанных в литературе алгоритмов [3–10] отличается не только характером и последовательностью операций, выполняемых в ходе фаззификации, нечеткого логического вывода и дефаззификации, но и видом используемых нечетких правил.
Методы Мамдани, Ларсена, Цукамото и product-sum-gravity оперируют нечеткими правилами, вид которых наиболее близок образу представления знаний человеком. Следовательно, формирование базы правил экспертом в случае использования этих методов будет наименее трудозатратным.
Методы Сугено, синглтона, упрощенного нечеткого вывода и SIRMs требуют от экспертов определения четких числовых значений и/или коэффициентов, что во многих предметных областях является нетривиальной задачей. Однако эти методы используют лишь простейшие арифметические операции, что дает выигрыш в вычислительной сложности по сравнению с первой группой методов.
Метод Цукамото накладывает требования к монотонности функций принадлежности выходных переменных, что во многих системах недопустимо.
Метод SIRMs требует при формировании базы правил группировать их в модули, кроме того, каждое правило должно содержать только одну входную переменную.
Отметим, что современные интеллектуальные системы, использующие механизмы нечеткого принятия решения, имеют базу знаний большой размерности, что требует использования специальных механизмов управления выводом для повышения эффективности принятия решения, в том числе для сокращения времени вывода. Описанные в литературе методы нечеткого вывода могут быть выполнены параллельно на нескольких вычислительных узлах, что может значительно снизить временные затраты на принятие решений в интеллектуальных системах. В данной статье предложены некоторые алгоритмы, позволяющие повысить эффективность принятия решения для продукционных баз знаний, использующих нечеткий вывод.
В нечетких базах знаний большой размерности распространены ситуации, когда обработать некоторое правило невозможно, предварительно не обработав ряд других правил. Например, такое ограничение появляется, когда среди посылок правила встречаются переменные, не подаваемые на вход системы, а получаемые в ходе выполнения других правил.
Для решения описанной проблемы предлагается метод определения очередности выполнения правил в базах правил с описанными выше особенностями.
На первом этапе сгенерируем матрицу зависимостей правил. Рассмотрим следующий алгоритм.
Алгоритм генерации матрицы зависимостей правил
Шаг 1. Инициализировать нулями квадратную матрицу DR размерностью |R|×|R| (где |R| – мощность множества R).
Шаг 2. Для каждого rj ∈ R выполнить Шаг 3.
Шаг 3. Для каждого rq ∈ R, rq ≠ rj выполнить Шаг 4.
Шаг 4. Если 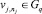 , то DRj,q = 1 и DRq,j = –1.
, то DRj,q = 1 и DRq,j = –1.
Полученная матрица DR является матрицей смежности для ориентированного графа зависимостей правил. Данный граф может быть использован для определения того, от обработки каких правил зависит выбор каждого конкретного правила в базе знаний.
Каждому правилу rj ∈ R поставим в соответствие значение функции ρ(rj), определяющее порядковый номер группы выполнения правил. Порядковый номер группы имеет следующий смысл: правило  не может быть выполнено раньше правила
не может быть выполнено раньше правила 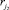 , если
, если 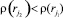 .
.
Алгоритм расчета функции ρ(rj), определяющей порядковый номер группы выполнения правил
Шаг 1. Инициализировать нулями множество RO, |RO| = |R|.
Шаг 2. j = 1.
Шаг 3. Если j ≤ |R|, то перейти к Шагу 4, иначе перейти к Шагу 10.
Шаг 4. i = 1.
Шаг 5. Если i ≤ |R|, то перейти к Шагу 6, иначе перейти к Шагу 8.
Шаг 6. Если DRj,i = –1, то перейти к Шагу 9.
Шаг 7. i = i + 1.
Шаг 8. roj = 1.
Шаг 9. j = j + 1. Перейти к шагу 3.
Шаг 10. j = 1, c = 0.
Шаг 11. Если j ≤ |R|, то перейти к Шагу 12, иначе перейти к Шагу 20.
Шаг 12. i = 1, m = 1.
Шаг 13. Если i ≤ |R|, то перейти к Шагу 14, иначе перейти к Шагу 17.
Шаг 14. Если DRj,i = –1, то перейти к Шагу 15, иначе перейти к Шагу 16.
Шаг 15. Если roi > m, то m = roi.
Шаг 16. i = i + 1. Перейти к Шагу 13.
Шаг 17. Если roj < m + 1, то c = 1.
Шаг 18. roj = m + 1.
Шаг 19. j = j + 1. Перейти к Шагу 11.
Шаг 20. Если c = 0, то перейти к Шагу 21, иначе перейти к Шагу 10.
Шаг 21. Для каждого rj: ρ(rj) = roj.
На основе полученных значений ρ(rj) формируются множества
RGm:rj ∈ RGm ⇔ ρ(rj) = m, 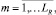
где LR – количество групп выполнения правил.
В ходе нечеткого логического вывода вычисляются не только результирующие функции принадлежности каждого отдельного правила rj, но и происходит дефаззификация лингвистических переменных. Очередность дефаззификации далеко не всегда связана с зависимостью между правилами базы знаний, т.к. каждая переменная может содержаться в посылках нескольких правил с различающимися порядковыми номерами групп выполнения ρ(rj).
Таким образом, возникает необходимость также определить наличие зависимостей между лингвистическими переменными. Рассмотрим следующий алгоритм генерации матрицы зависимостей лингвистических переменных.
Шаг 1. Инициализировать нулями квадратную матрицу DV размерностью |V|×|V|.
Шаг 2. Для каждого vk ∈ V выполнить Шаг 3.
Шаг 3. Для каждого vh ∈ V, vh ≠ vk выполнить Шаг 4.
Шаг 4. Для каждого rj ∈ R выполнить Шаг 5.
Шаг 5. Если vk ∈ Gj и 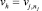 то DVk,h = 1 и DVh,k = –1.
то DVk,h = 1 и DVh,k = –1.
Полученная матрица DV может быть интерпретирована как матрица смежности ориентированного графа зависимости лингвистических переменных.
Каждой лингвистической переменной vk ∈ V поставим в соответствие значение функции ρ(vk), определяющее порядковый номер группы дефаззификации переменной. Порядковый номер группы имеет следующий смысл: переменная 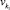 не может быть дефаззифицирована раньше переменной
не может быть дефаззифицирована раньше переменной 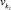 , если
, если 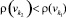 .
.
Алгоритм расчета функции ρ(vk), определяющей порядковый номер группы дефаззификации переменной
Шаг 1. Инициализировать нулями множество VO, |VO| = |V|.
Шаг 2. k = 1.
Шаг 3. Если k ≤ |V|, то перейти к Шагу 4, иначе перейти к Шагу 10.
Шаг 4. h = 1.
Шаг 5. Если h ≤ |V|, то перейти к Шагу 6, иначе перейти к Шагу 8.
Шаг 6. Если DVk,h = –1, то перейти к Шагу 9.
Шаг 7. h = h + 1.
Шаг 8. vok = 1.
Шаг 9. k = k + 1. Перейти к шагу 3.
Шаг 10. k = 1, c = 0.
Шаг 11. Если k ≤ |V|, то перейти к Шагу 12, иначе перейти к Шагу 20.
Шаг 12. h = 1, m = 1.
Шаг 13. Если h ≤ |V|, то перейти к Шагу 14, иначе перейти к Шагу 17.
Шаг 14. Если DVk,h = –1, то перейти к Шагу 15, иначе перейти к Шагу 16.
Шаг 15. Если voh > m, то m = voh.
Шаг 16. h = h + 1. Перейти к Шагу 13.
Шаг 17. Если vok < m + 1, то c = 1.
Шаг 18. vok = m + 1.
Шаг 19. k = k + 1. Перейти к Шагу 11.
Шаг 20. Если c = 0, то перейти к Шагу 21, иначе перейти к Шагу 10.
Шаг 21. Для каждого vk: ρ(vk) = vok.
На основе полученных значений ρ(vk) формируются множества
VGm:vk ∈ VGm ⇔ ρ(vk) = m, 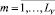 ,
,
где LV – количество групп выполнения переменных.
Подразумевается, что каждая переменная, для которой ρ(vk) = 1, является входной переменной (vk ∈ I) и не нуждается в дефаззификации.
На основе сформированных групп выполнения правил и дефаззификации лингвистических переменных планируется повысить эффективность процесса принятия решений за счет применения параллельных вычислений в пределах каждой группы. Эффективная параллельная обработка правил и переменных невозможна без предварительного разбиения на группы, т.к. зависимости (в т.ч. транзитивные) между ними зачастую позволяют обработать два правила только последовательно. Указанные алгоритмы были успешно применены для реализации механизма нечеткого вывода в экспертной системе обнаружения неисправностей газоперекачивающих агрегатов GAZDETECT [1].
Рецензенты:Кушников В.А., д.т.н., профессор, ведущий научный сотрудник, зам. директора по научно-организационной работе, Институт проблем точной механики и управления РАН, г. Саратов;
Шульга Т.Э., д.т.н., зав. кафедрой «Прикладная информатика и программная инженерия», международный факультет прикладных информационных технологий, Саратовский государственный технический университет им. Гагарина Ю.А., г. Саратов.
Работа поступила в редакцию 16.12.2014.



