Технические системы являются сложными, наделены множествами свойств, функций и требуют постоянного контроля над их состоянием. Эти обстоятельства обуславливают присутствие неопределенности информации по причине вероятностного протекания процессов. Применение теории информации не исключает возможностей оценивать состояние технической системы через меру неопределенности информации, включающую в себя информационную энтропию. Из-за многообразия состояний системы невозможно применить сколько-нибудь известные методы определения количества энтропии. Однако решение можно найти, пусть даже и с некоторыми допущениями, если рассматривать структуру системы. В этой сфере деятельности для оценки состояния системы через её структуру можно применить ряд математических инструментов определения количества информации. С количественным содержанием информации в технической системе можно ознакомиться в работах [1, 2, 9].
Если рассматривать структуру, то её элементы связаны между собой определенным образом и находятся в тот или иной момент времени в разнообразных вероятностных состояниях. При этом изменению подлежит и энтропия. Если принимать во внимание необходимость в определении количества информации, то в ряде задач целесообразно разделить информацию по качественному признаку на составляющие для целей последующего анализа. Например, когда рассматривают структурную надежность системы, разделяют состояния элементов на работоспособное и неработоспособное. Если решать подобную задачу с позиции меры неопределенности информации, то целесообразно информационную энтропию системы разделить по качественному признаку [6] с разграничением уровня надежности через показатель [3].
Прежде чем приступить к определению количества энтропии, следует построить модель выявления совместной и условной энтропий при рассмотрении событий, возникающих в системе, например отказ и работа элемента и системы. Такие модели предложены в [4, 5], реализация которых требует разработки методов. Одним из таких методов является метод перебора состояний (предложенный в [7]) и метод эквивалентирования последовательных и параллельных структур (представленный в [8]). Однако такие методы не применимы для сложнозамкнутых и многоэлементных структур. Поэтому востребован метод, который базировался бы на способе построения минимальных сечений структуры.
Рассмотрим далее математический метод минимальных сечений, позволяющий рассчитывать количество энтропии, присущей противоположным (непересекающимся) вероятностным состояниям элементов системы.
Определение энтропии методом минимальных сечений предполагает наличие показателей статистического ансамбля: время, в течение которого элемент находился в том или ином состоянии; частота появления тех или иных событий и др. Эти показатели позволяют рассчитать вероятности pi и qi = 1 – pi нахождения элемента i в двух противоположных состояниях. Если рассматривать состояние технической системы с позиции её структурной надежности, то pi и qi соответственно, вероятность работоспособного и неработоспособного состояний элемента i. Поскольку учитываются только два состояния, то можно определить информационную (статистическую) энтропию по Шеннону для одного элемента i по выражению
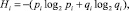 (1)
(1)
при условии pi + qi = 1. Здесь логарифм определения величины Hi в битах имеет основание, равное 2, что свидетельствует о рассмотрении двух противоположных состояний.
Для всей системы в целом, в предположении о независимом функционировании элементов системы, можно получить суммарную энтропию:
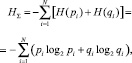 (2)
(2)
где N – число элементов в структуре системы. При всех pi = qi = 0,5, по (2) получим энтропию: HΣ = N.
Выражение (2) потребуется для проверки правильности выполненных расчетов энтропии противоположных состояний. Её количество следует рассчитать с учетом рассмотрения совместных событий в системе. Поэтому востребован метод, позволяющий рассчитывать качественные составляющие суммарной энтропии. Для определения её составляющих следует учесть не только число элементов N (состояния которых рассматриваются как независимые), но и топологию структуры системы. Если структура имеет замкнутый вид, то её следует преобразовать классическим методом минимальных сечений к виду «параллельно-последовательная структура».
Сформированные сечения, отраженные в виде параллельно-последовательной структуры, позволяют применить предлагаемый метод, который базируется на эквивалентных преобразованиях [8]. При реализации данного метода следует соблюсти условие: количество информации в исходной структуре должно быть равно количеству информации в сформированной параллельно-последовательной структуре. Дело в том, что количество элементов из-за их повторяемости в сформированной структуре будет больше чем в исходной структуре. Соблюдение данного условия выполняется следующим образом: количество энтропии каждого элемента k (во вновь созданной структуре) уменьшается на число его повторений.
Далее предложим порядок и применяемые математические выражения для расчета энтропии.
1. Рассчитывается энтропия по каждому из N элементов согласно (1):
– для работоспособного состояния элемента i –
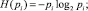 (3)
(3)
– для неработоспособного состояния элемента i –
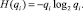 (4)
(4)
2. Рассчитывается энтропия по каждому из k элементов последовательно-параллельной структуры согласно:
– для работоспособного состояния
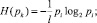 (5)
(5)
– для неработоспособного состояния
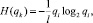 (6)
(6)
где l – количество повторений элемента i во вновь построенной структуре.
3. Для каждого сечения определяются вероятности:
– неработоспособного состояния элементов сечения j –
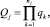 (7)
(7)
где qk – вероятность неработоспособного состояния элемента k, сечения j; nj – количество элементов, входящее в сечение;
– работоспособного состояния элементов сечения j –
Pj = 1 – Qj. (8)
4. По каждому из сечений определяются составляющие энтропии:
– неработоспособного состояния элементов сечения j –
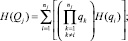 (9)
(9)
– работоспособного состояния элементов сечения j –
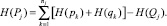 (10)
(10)
5. Определение энтропии системы:
– неработоспособного состояния –
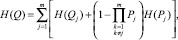 (11)
(11)
где m – количество сечений;
– работоспособного состояния –
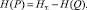 (12)
(12)
Пример. Следует определить методом минимальных сечений количество энтропии работоспособного и неработоспособного состояний мостиковой структуры, представленной на рис. 1.
Согласно рис. 1 множество всех состояний элементов 52 = 32. Неработоспособных состояний или сечений – 16. Из них минимальными являются сечения: {12}, {34}, {235}, {145}, количество которых – m = 4. Параллельно-последовательная структура из минимальных сечений представлена на рис. 2.
Примем значения pi = 0,9; qi = 1 – pi = 0,1, чтобы сопоставить конечные результаты энтропии со значениями, представленными в [8]. Представленные в процессе расчетов формулы отразим без перенумерации элементов сечений.
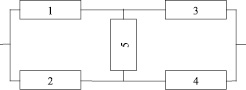
Рис. 1. Мостиковая структура (схема)
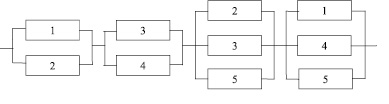
Рис. 2. Параллельно-последовательная структура (схема)
1. Определим по (3) и (4) энтропию элементов исходной схемы с N = 5 (рис. 1):
– для работоспособного состояния –
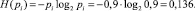
– для неработоспособного состояния –
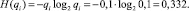
2. По выражениям (5) и (6) определим энтропии элементов параллельно-последовательной структуры, в которой каждый элемент i повторяется дважды:
– для работоспособного состояния –
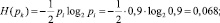
– для неработоспособного состояния –
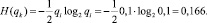
3. По выражениям (7) и (8) определяем для каждого из сечений вероятности:
– неработоспособного состояния:
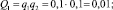
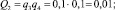
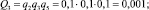
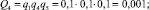
– работоспособного состояния:
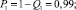
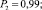
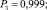
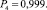
1. Согласно (9) и (10) определим составляющие энтропии каждого сечения:
– неработоспособного состояния:
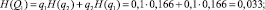
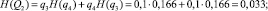
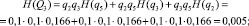
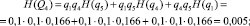
– работоспособного состояния:
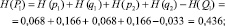
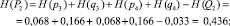
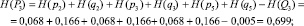
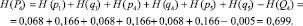
2. Определение по выражениям (11) и (12) энтропии системы:
– неработоспособного состояния:
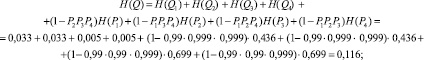
– работоспособного состояния:
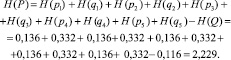
Из расчетов видно, что энтропия работоспособного состояния преобладает над энтропией противоположного состояния, поскольку вероятность работоспособного состояния выше, чем неработоспособного.
Сравним аналогичные результаты с представленными в работе [8]: H(P) = 2,169; H(Q) = 0,176; суммарная энтропия – HΣ = H(P) + H(Q) = 2,345.
Поскольку оба сравниваемых метода построены на предположении о независимости событий (возникающих в системе), то полученные по ним суммарные энтропии совпали, подтверждая тем самым справедливость предлагаемого метода. Однако между энтропиями состояний существует разница (между H(P) – 2,7 %, между H(Q) – 34 %). Ошибка обусловлена способом построения минимальных сечений, без учета множества других сечений.
Заключение
Представленный в работе метод служит для определения количества энтропии двух противоположных состояний. В качестве исходной структуры берется замкнутая, которая должна быть преобразована по способу выделения минимальных сечений в параллельно-последовательную структуру. Полученное количество энтропии отражает качественное и количественное содержание информации. Интеграция данного метода в среду оценки состояния системы (например, её структурной надежности) через меру неопределенности информации позволит выполнить сопоставительные оценки между противоположными состояниями системы.
Рассматривая различные варианты структур системы, используя предлагаемый метод, можно выбрать более надежную или эффективную структуру с позиции наличия в ней определенного количества информационной энтропии.
Работа выполнена при поддержке гранта РФФИ № 15-08-01473а.



