Как известно, термин «кавитация» употребляется как при описании гидродинамических, так и акустических эффектов [14, 18, 34]. Гидродинамическая кавитация представляет собой возникновение и развитие разрывных течений жидкостной среды (при образовании, росте, сжатии и схлопывании пузырей для системы газ – пар) в зоне пониженного давления при достижении некоторого критического значения скорости ее потока, акустическая – соответствует распространению акустических волн. Явление кавитации относится к эффектам с последствиями, имеющими двоякий характер в зависимости от функционального назначения процесса, в рамках которого проявляется. С одной стороны, в технике кавитация может оказывать нежелательное действие при работе различных гидравлических механизмов (эрозийные разрушения поверхностей каналов течения, значительный шум вне санитарных норм эксплуатации оборудования) [16]. С другой стороны, новые конструкторские решения насосов и винтов позволяют использовать явление суперкавитации (распространения одной каверны из слившихся малых пузырей на расстояния, много большие, чем местные сопротивления) [10], в области процессов химических технологий – применять кавитацию в операциях смешивания [24] и растворения [5] рабочих сред, очистки эмульсий [25], в том числе пищевых продуктов [21], для снижения вязкости нефтепродуктов [9] и т.д. При проектировании регулирующих органов трубопроводов необходимо учитывать одно из основных требований эксплуатационных норм [7, 8] – снижение влияния кавитационных эффектов на течение транспортируемых сред с целью повышения основных характеристик данных устройств (пропускной и расходной), а также предотвращения эрозии, шума (например, > 85 дБ) и вибраций в арматуре.
Цель работы: анализ современных методов определения критических параметров кавитации в регулирующих органах при транспортировании рабочих сред.
Об основных способах борьбы с кавитационными эффектами в регулирующих органах
Напомним, что одним из элементов трубопроводной арматуры является регулирующий орган, который как гидравлическое устройство может выполнять несколько функций в цепи трубопровода – непосредственно регулирование потоками рабочей среды (с целью исключения обратных протечек, сброса повышенного или поддержания заданного уровня давления), их смешивание, перекрытие, разделение [6, 27]. Способность клапанов управлять изменениями давления и расхода среды характеризует назначение данного оборудования как дросселирующего.
Различают три режима течения жидкости (ламинарный, переходный и турбулентный), которые соответствуют определенным диапазонам изменения числа Рейнольдса Re = wL/v, где w и ρ – усредненная скорость среды; ее плотность; L – характерный размер прямолинейного участка; 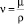 – динамическая и μ – кинематическая вязкости. Область течений жидкости, в которой одновременно реализуются два крайних режима, еще называют критической. Например, в соответствии с данными из работы [1] для односедельного клапана перечисленные области течений жидкостей соответствуют пределам: Re ≤ 10; 10 < Re < 104; Re ≥ 104; для двухседельного: Re ≤ 10; 10 < Re < 5·102; Re ≥ 5·102.
– динамическая и μ – кинематическая вязкости. Область течений жидкости, в которой одновременно реализуются два крайних режима, еще называют критической. Например, в соответствии с данными из работы [1] для односедельного клапана перечисленные области течений жидкостей соответствуют пределам: Re ≤ 10; 10 < Re < 104; Re ≥ 104; для двухседельного: Re ≤ 10; 10 < Re < 5·102; Re ≥ 5·102.
Появление критической области потока жидкости в проточной части регулирующего органа еще не означает реализацию негативных последствий кавитации [14, 18], требуется выявить характерные диапазоны изменения давления Δp, скорости, плотности среды. К образованию паровых пузырей при проходе рабочей жидкостной среды через проточную часть регулирующего органа приводит значительное падение давления (до значений ниже давления насыщенного пара pн) вследствие дросселирования или смены направления течения при обтекании препятствий. Для сравнения, известно, что при температуре 100 °С давление насыщенного водяного пара
pн = 760 мм рт. ст. = 1 бар = 10–1 МПа,
а при 20,8 °С значение
pн = 18,75 мм рт. ст. = 2,5·10–2 бар = = 2,5·10–3 МПа [16].
Попадание образовавшихся пузырей в область высоких давлений течения рабочей среды приводит к их схлопыванию при достижении локальных значений: давления в пределах (104–105) бар = (103–104) МПа; температуры до 103 °С; скоростей потоков до 103 м/c. На первый взгляд, можно было бы воспользоваться только критерием Эйлера 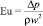 для оценки стадии эволюции гидродинамической кавитации, а при акустической – критерием Маха M = w/a, где a – местная скорость звука. Однако эти вопросы связаны с выбором критических параметров кавитации и требуют более детального подхода.
для оценки стадии эволюции гидродинамической кавитации, а при акустической – критерием Маха M = w/a, где a – местная скорость звука. Однако эти вопросы связаны с выбором критических параметров кавитации и требуют более детального подхода.
Кратко остановимся на основных способах борьбы с кавитационными эффектами при проектировании регулирующих клапанов [1, 6, 20, 23, 27]. Первый относится к уменьшению области турбулентности и предотвращению контакта пузырей с внутренними поверхностями каналов, в частности, за счет расширения выходного патрубка регулирующего устройства и т.д. Второй – к управлению потоками среды благодаря поэтапному достижению необходимого перепада давления или разделению потока заменой одного проходного сечения несколькими с меньшими размерами [20]. Избежание резкого падения давления при течении жидкостей достигается, например, при использовании: нескольких ступеней в конструкции плунжера (затвора устройства) [1] или его перфорированного цилиндра; дроссельных щелей в неподвижной (седельной) и подвижной (золотниковой) частях затвора для образования радиальных проходных сечений при повороте золотника [13, 15] и т.д. В работе [16] анализируются и другие конструктивные методы указанного назначения. Для газовых потоков также применяются принципы: многоступенчатости их дросселирования и интенсификации последнего с помощью дополнительных распределителей в виде сеток, перфорированных дисков, цилиндров [11, 17] и т.п. Заметим, что применение указанных дополнительных регулирующих элементов для сред с примесями в виде твердой фазы может, напротив, осложнить работу регулирующего органа.
Понятие о традиционных критических параметрах кавитации для регулирующих органов
Во многих литературных источниках вводится понятие «число кавитации κ» как параметр, характеризующий кавитационные свойства местных сопротивлений (или регулирующего органа) [1, 14, 18]:
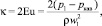 (1)
(1)
где p1 = pатм + pман – абсолютное давление в стационарном потоке жидкостной среды на входе, которое складывается из давлений – атмосферного и манометрического за устройством управления расходом; pкав – давление в кавитационном пузыре.
Согласно работам [15, 18] физический смысл числа кавитации κ соответствует отношению перепада давления жидкости, приводящего к схлопыванию пузыря, к изменению скорости среды, а следовательно, и к падению ее давления, при котором наблюдается образование и рост данного пузыря.
При выполнении (1) и условия pкав = pн (равенства между давлениями в пузыре и насыщенного пара рабочей жидкости) для практических расчетов применяется критический параметр кавитации κi (соответствующий достижению значения pкав – минимального давления в потоке), определяемый по формуле
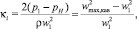 (2)
(2)
где wmax,кав – максимальная скорость течения среды в условиях кавитации.
При этом считается [1, 2, 15, 18, 22 и др.], что соотношение между параметрами κ и κi характеризует стадию эволюции кавитационного явления в потоке жидкостной среды. Достижение критического значения κi в этом случае соответствует начальной стадии кавитации, а возврат к условию вида κ < κi предполагает развитие нового ее этапа. Например, как уже отмечалось во введении, последнее условие отражает появление суперкавитации, которая может быть искусственно создана вдуванием воздуха, что отражено в работах [31, 33] при описании выбора критерия перехода от одной формы каверны к другой.
На практике для определения значения минимального критического числа кавитации в проточной части регулирующих органов, а также выявления зоны кавитации особый интерес представляет зависимость коэффициента гидравлического сопротивления для проходного сечения ζпр = ζпр(κ) или для условного прохода ζу = ζу(κ) от числа кавитации κ. Напомним, что для потока жидкостной среды справедлива формула Вейсбаха 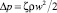 [1, 6, 27], отражающая взаимосвязь перепада давления Δp с другими параметрами течения. Обычно графическая зависимость ζу = ζу(κ) представляет собой кривую приближенно экспоненциального характера, которую можно разбить на два характерных участка по этапам эволюции кавитации: практическая стабилизация значений ζу при κ > κi (безкавитационный режим) и возрастание значений ζу до резкого скачка при κmin,i ≤ κ ≤ κi (кавитационные течения). При этом минимальное критическое число кавитации κmin,i соответствует пиковому значению ζу и максимально достижимому расходу жидкости Qкав.max через регулирующее устройство.
[1, 6, 27], отражающая взаимосвязь перепада давления Δp с другими параметрами течения. Обычно графическая зависимость ζу = ζу(κ) представляет собой кривую приближенно экспоненциального характера, которую можно разбить на два характерных участка по этапам эволюции кавитации: практическая стабилизация значений ζу при κ > κi (безкавитационный режим) и возрастание значений ζу до резкого скачка при κmin,i ≤ κ ≤ κi (кавитационные течения). При этом минимальное критическое число кавитации κmin,i соответствует пиковому значению ζу и максимально достижимому расходу жидкости Qкав.max через регулирующее устройство.
Заметим, что анализ условий достижения Qкав.max выполняется гидродинамическим методом. Графическое представление объемного расхода жидкости (согласно определению 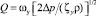 , где ωу – площадь сечения условного прохода) соответствует функции
, где ωу – площадь сечения условного прохода) соответствует функции 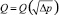 и, как правило, также используется для выявления условных этапов развития кавитации: участок прямой пропорциональности возрастания указанного расхода
и, как правило, также используется для выявления условных этапов развития кавитации: участок прямой пропорциональности возрастания указанного расхода 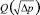 с ростом аргумента
с ростом аргумента 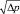 до точки перегиба
до точки перегиба 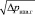 и участок выхода на постоянный расход рабочей среды при продолжающемся возрастании значений
и участок выхода на постоянный расход рабочей среды при продолжающемся возрастании значений 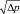 [6, 27, 23]. Здесь Δpкав.г – перепад давлений, определяемый гидродинамическим методом [26] (по указанному графику
[6, 27, 23]. Здесь Δpкав.г – перепад давлений, определяемый гидродинамическим методом [26] (по указанному графику 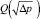 в точке перегиба).
в точке перегиба).
Об альтернативных способах оценки критических параметров кавитации для регулирующих устройств
Однако результаты экспериментальных исследований течений жидкости в условиях кавитации с привлечением не гидродинамических, а виброакустических методов [30] показали, что явление кавитации проявляется значительно раньше, чем при Δpкав.г, т.к. выявлено нарушение линейного характера описанного участка зависимости 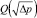 . В связи с этим обстоятельством в литературных источниках [4, 26] дискутируется вопрос о целесообразности применения дополнительных критических параметров кавитации, к которым согласно подходу [35] традиционно относятся: «коэффициент начальных стадий кавитации» Kc и «коэффициент кавитации или критического расхода» Km, определяемые по формулам [1, 6, 22, 23 и др.]
. В связи с этим обстоятельством в литературных источниках [4, 26] дискутируется вопрос о целесообразности применения дополнительных критических параметров кавитации, к которым согласно подходу [35] традиционно относятся: «коэффициент начальных стадий кавитации» Kc и «коэффициент кавитации или критического расхода» Km, определяемые по формулам [1, 6, 22, 23 и др.]
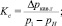 (3)
(3)
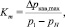 (4)
(4)
где Δpкав.max – перепад давлений, соответствующий минимальному критическому числу кавитации κmin,i, т.е. когда расход жидкости через регулирующее устройство достигает значения Qкав.max и стабилизируется. Причем, как отмечается авторами [4, 26], указанные критические параметры кавитации Kc и Km используются в отечественных стандартах, но в соответствии с результатами работы [30] отменены в международном стандарте [32].
В частности, в работе [4] внесены предложения по применению вместо параметров Kc и Km из (3) и (4) одной характеристики, например KR,c – степени «восстановления» давления в сжатом сечении регулирующего органа
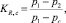 (5)
(5)
где p1, pс ≡ p3, p2 – давления среды во входном «1», суженном (щелевом) «3» и выходном «2» сечениях ω1, ω3, ω2. В статье [26] анализируются условия бескавитационной работы регулирующего устройства согласно требованию KR,c → 1 и предлагается способ расчета значения данного параметра с числом ступеней дросселирования, равным n, при условии одинаковых значений степени «восстановления» давления KR,c,др на каждой из ступеней:
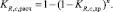 (6)
(6)
Заметим, что анализ гидродинамики в регулирующих органах, включающий расчет пропускной и расходной характеристик, основан на определении функциональных зависимостей: пропускной способности 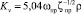 ; коэффициента гидравлического сопротивления для проходного сечения ζпр (или условного прохода ζу) согласно формуле Вейсбаха; коэффициента расхода среды – аналогично
; коэффициента гидравлического сопротивления для проходного сечения ζпр (или условного прохода ζу) согласно формуле Вейсбаха; коэффициента расхода среды – аналогично 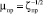 (или
(или 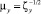 ) от критериев Рейнольдса, Эйлера, Струхаля и Маха, а также описанных ранее критических двух параметров кавитации Kc и Km [2, 6, 27] или одного – KR,c [4, 26].
) от критериев Рейнольдса, Эйлера, Струхаля и Маха, а также описанных ранее критических двух параметров кавитации Kc и Km [2, 6, 27] или одного – KR,c [4, 26].
О взаимосвязи коэффициента гидравлического сопротивления и критических параметров кавитации для регулирующих устройств
Как уже отмечалось, вид зависимости коэффициента гидравлического сопротивления для проходного сечения ζпр = ζпр(κ) или для условного прохода ζу = ζу(κ) от числа кавитации κ играет значительную роль при определении значений критических параметров кавитации κi гидродинамическим методом. В литературных источниках имеются разнообразные выражения для связи между значениями κi из (2) и коэффициентом сжатия жидкостной рабочей среды ε = ε(n) в различных случаях ее течений, полученные на основе уравнения непрерывности, где параметр 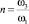 – степень сжатия потока [1]:
– степень сжатия потока [1]:
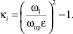 (7)
(7)
Справочные пособия по трубопроводной арматуре [1, 6, 12] содержат разнообразные формулы для расчета параметра κi как для простых случаев течений – в трубах с острыми и плавными входными кромками, конфузорных переходах, коленах и отводах, так и для регулирующих устройств – заслоночных, односедельных, двухседельных и т.д. Для различных форм плоских щелей используются полуэмпирические формулы [1, 6, 12]: при круглом сечении 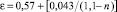 (А.Д. Альтшуль) или ε = 0,611 + 0,148n2 (В.В. Ведерников); с особой формой кромок
(А.Д. Альтшуль) или ε = 0,611 + 0,148n2 (В.В. Ведерников); с особой формой кромок 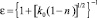 (К.В. Химицкий, k0 = 0,4 – для острых,
(К.В. Химицкий, k0 = 0,4 – для острых, 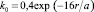 – для скругленных радиусом r со средним размером стороны отверстия a); для колена трубы
– для скругленных радиусом r со средним размером стороны отверстия a); для колена трубы 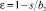 (И.Е. Идельчик, b2 – ширина выходной части колена); конфузора
(И.Е. Идельчик, b2 – ширина выходной части колена); конфузора 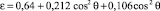 (формула Вейсбаха – Цейнера, θ – угол конусности) и др.
(формула Вейсбаха – Цейнера, θ – угол конусности) и др.
Например, в результате применения (7) и формулы К.В. Химицкого с учетом коэффициента абсолютной шероховатости kэ, а также различных скругленных радиусов седел r1 и r2 получены следующие выражения для искомого параметра κi соответственно для потоков жидкости под затвор (плунжер) и на затвор [2]:
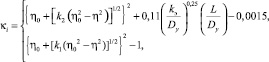 (8)
(8)
где
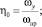
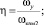
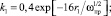
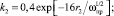
характерные размеры – для прямолинейных участков L и проходов условного (номинального диаметра входного патрубка) Dу; площади сечений для камеры после расширения (сужения) потока ωкан2; проходного ωпр и условного прохода ωу.
Кроме того, могут быть установлены функциональные зависимости вида 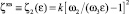 в квадратичной области гидравлического сопротивления (т.е. при Re ≥ 104) [1]. Тогда, в частности, учитывая принцип суперпозиции для потерь давления при течении жидкости через проточную часть углового односедельного регулирующего устройства, в работе [2] получены выражения для связи между κi и ζкв для потоков среды под затвор (плунжер) и на затвор
в квадратичной области гидравлического сопротивления (т.е. при Re ≥ 104) [1]. Тогда, в частности, учитывая принцип суперпозиции для потерь давления при течении жидкости через проточную часть углового односедельного регулирующего устройства, в работе [2] получены выражения для связи между κi и ζкв для потоков среды под затвор (плунжер) и на затвор
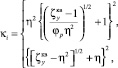 (9)
(9)
где значение угла расширения для поворота потока меняется в пределах
φp = (0,08 – 0,52);
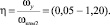
В работах [3, 4] получены выражения для KR,c – степени «восстановления» давления в сжатом сечении для бескризисного турбулентного режима течения жидкости в трубе Вентури согласно определению (5) в двух случаях: для произвольного сечения i трубопроводного сужающегося устройства
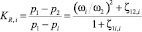
и для входного участка до сжатия струи (в сечении «c-c», аналогичного ранее введенному сечению ω3) при максимальной скорости потока
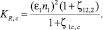
Здесь: 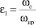 – коэффициент сжатия струи по отношению к лимитирующему проходному сечению ωпр;
– коэффициент сжатия струи по отношению к лимитирующему проходному сечению ωпр; 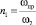 – степень сужения струи по отношению к выходному сечению ω2; ζ1c,c – коэффициент гидравлического сопротивления для входного участка до сжатия струи (в сечении «c-c»); ζ12,2 – коэффициент гидродинамического сопротивления между сечениями ω1 и ω2, отнесенный к выходной скорости потока w2.
– степень сужения струи по отношению к выходному сечению ω2; ζ1c,c – коэффициент гидравлического сопротивления для входного участка до сжатия струи (в сечении «c-c»); ζ12,2 – коэффициент гидродинамического сопротивления между сечениями ω1 и ω2, отнесенный к выходной скорости потока w2.
Отметим активное использование численного моделирования при определении коэффициентов начала кавитации в регулирующих устройствах, в частности при проектировании бескавитационного регулятора давления шарового типа [19] с пересекающимися перфорированными перегородками, образующими многокамерный рабочий объем. Кроме того, в работе [28, 29], применяя программный комплекс ANSYS, разработана методика регулирования расположения кавитационной зоны за запорным узлом для шиберных задвижек при действии стабилизатора, основанная на расчете диаметра отверстий между стабилизатором и шибером согласно технологическим условиям.
Заключение
Таким образом, оценка критических параметров кавитации в регулирующих органах при транспортировании рабочих сред является актуальной проблемой, связанной с проектированием соответствующего бескавитационного трубопроводного оборудования. Кратко проанализированы способы предотвращения появления кавитационных эффектов при работе трубопроводной регулирующей арматуры, которые в основном базируются на применении принципов многоступенчатости операции дросселирования потоков среды и его интенсификации с помощью дополнительных разгружающих элементов. Выявлены различные подходы к формированию набора гидродинамических показателей для описания поведения потоков жидкостей в проточных частях данных устройств. В анализируемых работах отечественных и зарубежных авторов для указанных целей используются гидродинамический и акустический методы. На примерах из литературных источников показана взаимосвязь между коэффициентом гидравлического сопротивления и критических параметров кавитации для регулирующих устройств.



