Разработка и исследование источников альтернативной энергии является важной и актуальной научно-технической задачей. Наибольшие перспективы в этой области связывают с фотоэлектрическими преобразователями на основе простых [1] и сложных полупроводников [2]. Основными методами получения солнечных элементов являются молекулярно-лучевая эпитаксия [3], газофазное осаждение [4] и ионно-лучевая кристаллизация [5]. Для исследования их морфологии часто применяют методы зондовой микроскопии [6]. Ранее нами метод ионно-лучевой кристаллизации был использован для выращивания кремниевых слоев [7], квантово-размерных гетероструктур в системе Ge/Si [8] и InAs/GaAs [9]. Параллельно с решением технологических задач нами проводилось также моделирование зависимостей функциональных характеристик солнечных элементов на основе аморфного кремния [10] и квантово-размерных гетероструктур [11]. Цель предлагаемой работы заключается в проведении численного моделирования и оптимизации функциональных характеристик монокристаллических кремниевых фотоэлектрических преобразователей.
Моделирование проводилось для спектрального состава солнечного излучения АМ 1.5 в спектральном диапазоне от 300 до 1200 нм, освещение осуществлялось с фронтальной части. В качестве контактов были выбраны идеальные контакты Шоттки (работа выхода электронов принималось равной 4,05 эВ для фронтального и тыльного контактов). Скорость поверхностной рекомбинации электронов и дырок Sn и Sp на границе контактов Шоттки равнялась 107 см/с. В процессе моделирования варьировалась температура окружающей среды от 250 до 350 К; толщина фронтального слоя с-Si(n) от 300 до 500 нм, концентрация основных носителей заряда Nd от 1016 до 1019 см–3. Толщина тыльного слоя р варьировалась в диапазоне от 10 до 500 мкм и концентрация носителей заряда Na от 1016 до 1018 см–3. Ширина запрещенной зоны составляла 1,124 эВ. Для с-Si(n) были использованы следующие параметры: подвижность электронов µn = 119,5 см2/В·с, подвижность дырок µр = 159,9 см2/В·с, а для тыльного слоя с-Si(p) подвижность электронов µn = 1041 см2/В·с и подвижность дырок µр = 412,9 см2/В·с. Длины свободного пробега для всех слоев Ln = 0,246 мкм и Lр = 0,398 мкм.
Моделирование проводилось на основе стандартной «диффузионно-дрейфовой» одномерной модели. В этой модели совместно решается система одномерных уравнений с использованием дискретной сетки. Система представлена уравнением Пуассона и двумя уравнениями переноса заряда в случае электронов и дырок.
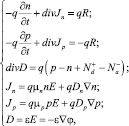 (1)
(1)
где q – заряд электрона; Е – напряженность электрического поля; Dn – диффузионный коэффициент для электрона; Dp – диффузионный коэффициент для дырки; ε – диэлектрическая проницаемость. φ = φ(x, t), n = n(x, t) и p = p(x, t), которые должны быть решены в ограниченной области Ω ⊂ Rq, q = 1, 2, 3. Моделирование проводилось в свободно распространяемой программе AFORS–HET 2.5.
Уравнение вольтамперной характеристики имеет вид
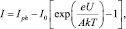 (2)
(2)
где Iph – плотность фототока; I0 – плотность тока насыщения; А – диодный коэффициент; T – температура; k – постоянная Больцмана; e – заряд электрона; U – напряжение.
Ток короткого замыкания численно равен фототоку:
Iкз = Iph. (3)
Напряжение холостого хода находится через величину фототока:
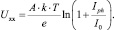 (4)
(4)
Важнейшей характеристикой солнечных элементов является КПД. КПД определяет эффективность преобразования энергии солнечного излучения в электрическую энергию:
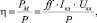 (5)
(5)
где Р – мощность падающего на СЭ солнечного излучения, приходящаяся на единицу поверхности СЭ; РМ – максимальная выходная мощность СЭ, отнесенная к площади поверхности; ff – коэффициент (фактор) заполнения или коэффициент формы ВАХ. Фактор заполнения показывает, какая часть мощности, вырабатываемая СЭ, используется в нагрузке и определяется как [6]
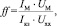 (6)
(6)
где IМ и UМ – плотность тока и напряжения, соответствующая наибольшей мощности PМ.
Результаты численного моделирования влияния уровня легирования доноров Nd в фронтальном слое с-Si(n) при неизменной толщине d = 300 нм на вольтамперную характеристику приведены на рис. 1.
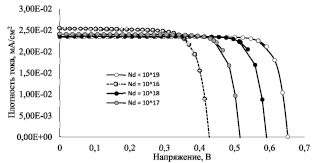
Рис. 1. Зависимость ВАХ моделируемого солнечного элемента от уровня легирования фронтального слоя
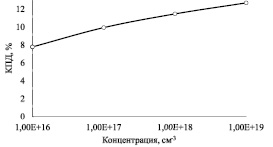
Рис. 2. Зависимость КПД моделируемого солнечного элемента от уровня легирования фронтального слоя с-Si(n)
Оптимальное значение уровня легирования фронтального слоя с-Si(n) можно определить из рис. 2.
Анализ полученных графических и численных данных показывает, что увеличение уровня легирования фронтального слоя с 1016 до 1019 см–3 приводит к небольшому спаду тока короткого замыкания Iкз и увеличению КПД. Зависимость напряжения холостого хода Uxx от уровня легирования фронтального слоя носит значительный характер. Так, при изменении уровня легирования фронтального слоя в указанном диапазоне напряжение холостого хода уменьшилось на 0,23 В.
Установлено, что изменение уровня легирования Nd оказывает большее влияние на напряжение холостого хода Uxx, чем на ток короткого замыкания Iкз. В диапазоне концентрации 1016–1019 см–3 повышается Uxx 0,43 до 0,65 В и снижается Iкз с 25,4 до 23,37 мА/см2. Установленные закономерности объясняются логарифмической зависимостью Uxx и обратно пропорциональной зависимостью Iкз от собственной концентрации доноров Nd. В совокупности повышение Nd приводит к возрастанию КПД с 8,2 до 12,7 %.
Результаты моделирования влияния уровня легирования акцепторов Na в тыльном слое с-Si(р) при неизменной толщине d = 300 мкм на эффективность солнечного преобразователя показаны на рисунке 3.
Анализ полученных графических и численных данных показывает, что увеличение уровня легирования тыльного слоя с 1016 до 1018 см–3 приводит к незначительному увеличению тока короткого замыкания Iкз. КПД немного увеличивается, с 11 до 12,6 %. Можно видеть, что зависимость напряжения холостого хода Uxx от уровня легирования тыльного слоя носит слабый характер и уменьшается на 50 мВ. Установлено, что изменение уровня легирования акцепторов Nа оказывает небольшое увеличение напряжения холостого хода Uxx и тока короткого замыкания Iкз. В диапазоне концентрации 1016–1018 см–3 повышается Uxx 0,6 до 0,65 В и снижается Iкз с 22,2 до 23 мА/см2.
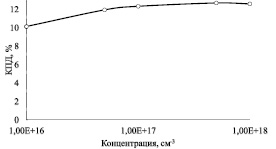
Рис. 3. Зависимость КПД моделируемого солнечного элемента от уровня легирования тыльного слоя с-Si(р)
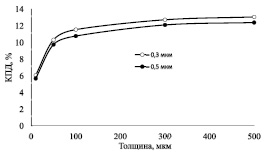
Рис. 4. Зависимость КПД моделируемого солнечного элемента от толщины тыльного слоя с-Si(р) при разной толщине фронтального слоя с-Si(n)
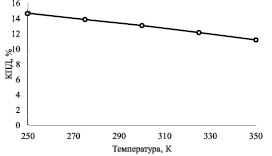
Рис. 5. Зависимость КПД моделируемого солнечного элемента от температуры окружающей среды
Результаты численного моделирования влияния толщины d тыльного слоя с-Si(р) на КПД представлены на рис. 4.
Технологически оправдано выращивать фронтальные слои толщиной d от 100 до 300 нм. При больших значениях толщины КПД моделируемого солнечного элемента становится менее 13 %. Слои тоньше 100 нм достаточно сложно получить. Поэтому оптимальной толщиной фронтального слоя будем считать 300 нм. При толщине тыльного слоя, равной 500 мкм, достигается максимальный КПД исследуемого солнечного элемента.
На рис. 5 графически представлена зависимость изменения температуры окружающей среды на КПД исследуемого солнечного элемента со следующими характеристиками: Nd = 1019 см–3, Nа = 5·1017 см–3, толщина фронтального слоя с-Si(n) равна d = 300 нм и толщина тыльного слоя с-Si(р) равна d = 300 мкм.
Выводы
Таким образом, в программе AFORS–HET 2.5 на основе диффузионно-дрейфовой модели Шокли – Рида – Холла было проведено численное моделирование влияния толщины d, температуры T и уровня легирования Nd фронтального и Na тыльного слоя на функциональные характеристики кремниевых солнечных элементов c–Si(n)/c–Si(p). Получены и проанализированы зависимости вольтамперных характеристик от параметров фронтального и тыльного слоя d, T, Nа и Nd. Установлено, что при толщине фронтального слоя d = 300 нм и толщине тыльного слоя d = 500 мкм КПД моделируемого солнечного элемента достигает максимального значения, равного 14 % при концентрации доноров Nd = 1019 см–3 и концентрации акцепторов Na = 5·1017 см–3 при температуре окружающей среды T = 250 K. Следует отметить, что КПД реальных солнечных элементов может быть меньше расчетных на 3–5 % [10], так как что на экспериментальных моделях появляются некоторые погрешности, которые не описываются формулами в аналитической модели. Поэтому на практике следует ожидать КПД у реальных солнечных элементов порядка 12–13 %.
Работа выполнена при поддержке гранта Президента Российской Федерации для государственной поддержки молодых российских ученых МК-5115.2016.8.



