Для расчета процентного содержания активов в портфеле применяют различные методы оптимизации. Рассмотрим основные оптимизационные методы.
Детерминистический контроль
Рассмотрим квадратично-линейный метод отслеживания траектории, который имеет следующий вид: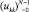 
Целью является минимизирование функционала стоимости:
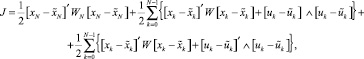
где xk = вектор состояния – вектор n;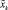 
= необходимый вектор состояния – вектор 
.
Алгоритм Нелдера - Мида
Данный алгоритм прост, но не быстр и не надежен. При решении многих задач проблема оптимизации, являющаяся частью более крупной проблемы, должна неоднократно решаться с незначительным изменением параметров функции при каждой итерации. Для решения таких задач, общих для динамических моделей, обычно предпочитают использовать метод, позволяющий более быстро и точно продвигаться к оптимуму с заданной хорошей начальной точкой.
Рассмотрим применение алгоритма оптимизации Нелдера – Мида к множеству глобальных минимумов. Для произвольно взятой функции h:D → R при D ⊂ Rm найдем точки
x* ∈ D,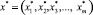 
,
при которых
x* = arg min h(w),
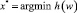, w ∈ D.
Таким образом,
h(x*) = min h(x), x ∈ D, (1)
где x = (x1, x2, x3, …, xm).
Фактически h(x*) представляет собой глобальный минимум функции h(x), x ∈ D. Для определения глобального минимума h(x*) часто применяются классические методы оптимизации с использованием производной, основанные на направлении градиента. Но на практике точное выражение функции градиента всегда чрезвычайно сложно определить. Поэтому выражение градиента часто аппроксимируется по конечным разностям.
В методах без использования производной непосредственно применяются только некоторые выбранные значения h(x).
Метод NM ориентирован на решение проблемы непрерывной неограниченной оптимизации типа (1).
Гибкость алгоритма, построенного по принципу NM, задается его четырьмя параметрами α, β, γ, δ, которые направляют процесс на поиск глобального минимума функции.
Рассмотрим применение алгоритма NM. В итеративных процедурах оптимизации в целом используется только начальная точка x1 ∈ D, которая определяется в соответствии со специальными правилами.
Алгоритм NM за начальную форму принимает D ⊂ Rm. Для любых двух точек y ∈ Rm и z ∈ Rm можно получить новую точку w ∈ Rm путем использования λ-правила, что имеет следующий вид:
w = z + λ(y – z), λ ∈ R.
Таким образом, если y = (y, y, y, …, ym), z = (z, z2, z, …, zm), w = (w1, w2, w, …, wm), мы получаем
wj = zj + λ(yj – zj), 1 ≤ j ≤ m.
В данном варианте параметры λ имеют следующие значения:
α = 1, β = 2, γ = 0,5, δ = 0,5.
Алгоритм Бройдена - Флетчера - Гольдфарба - Шанно (BFGS)
Рассмотрим алгоритм оптимизации на основе метода BFGS. Выберем начальное приближение х0, начальное приближение гессиана Н0 = 1 и параметры остановки δ и ε >0.
Шаг 1. Решим Hksk = –(∇f(xk))T для направления поиска sk.
Шаг 2. Решим λk = arg min λ f(xk + λsk).
Шаг 3. xk+1 = xk + λksk.
Шаг 4. Обновим Hk:
zk = xk+1 – xk;
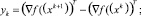
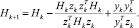(2)
Шаг 5. Если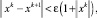 
перейти к шагу 6; иначе перейти к шагу 1.
Шаг 6. Если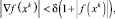 
остановиться и доложить о выполнении; иначе остановиться и доложить о схождении к неоптимальной точке.
Эта последовательность Hk является положительно определенной и симметричной настолько, насколько симметрично Н0. Общим выбором для Н0 является матрица тождественности. В этом случае первый шаг такой же, как и шаг наискорейшего спуска. Если система не слишком большая, Н0 может быть задан равной гессиану в х0, при этом первый шаг должен быть таким же, как и в методе Ньютона с линейным поиском. Так как все Hk являются положительно определенными, для выполнения решения в шаге 1 для направления поиска можно использовать разложение Холецкого.
Уравнение (2) представляет собой усовершенствование метода BFGS, а именно метод Дэвидона - Флетчера - Пауэлла (DFP), при котором уравнение (2) заменяется на (3):
Оптимизация:
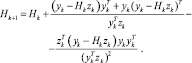(3)
Как показывает общая практика, метод BFGS работает чаще, чем метод DFP, однако при этом последний в некоторых случаях является более эффективным.
В алгоритмах гессиан-обновления последовательность Hk при решении не обязательно сходится к истинному гессиану. Таким образом, в случае необходимости гессиан должен вычисляться в конце. Одним из таких случаев является вычисление формулы оценки с использованием метода максимального правдоподобия, когда гессиан используется для составления выводов. Так как конечный гессиан в любом случае должен вычисляться в подобном эконометрическом контексте, то когда процедура оптимизации очевидно сходится в одной точке, необходимо переходить на метод Ньютона. Это несложно: если проблема сходится в одной точке, будет достаточно одной итерации по методу Ньютона; если требуется больше, это свидетельствует о том, что поиск следует продолжать. Таким образом, были рассмотрены основные методы оптимизации инвестиционного портфеля.
Эффективность портфеля ценных бумаг в теории риска
Рассмотрим один из методов определения эффективности инвестиционного портфеля, основанный на теории риска. Введем основополагающий критерий VAR, описывающий статистическую меру риска. Данный критерий снижает риск падения курса от выбранных факторов риска, с заданным уровнем доверительной вероятности и устойчивым инвестиционным горизонтом. Портфель со стоимостью Х, состоящий из n активов, каждый из которых имеет прибыльность rt, (t = 1, 2, ..., n), и весом портфеля ωt, rt (t = 1, 2, ..., n), уровнем доверительной вероятности d и периодом владения h, значение рисковой стоимости портфеля VaR со значением VaRd, h на уровне доверительной вероятности d и инвестиционным промежутком времени h, определяется следующей формулой:
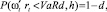
где Р(.) – плотность распределения вероятности.
В течение многих лет в экономике упоминались три основных подхода, а именно: параметрический, непараметрический и полупараметрический. Параметрический подход основан на дифференцировании аналитической формы при ограниченных условиях и обладает свойством разрешимости в модельной конструкции. Эталоны сравнения – многомерное экспоненциально-взвешенное скользящее среднее (MEWMA) и многомерная обобщенная авторегрессионная модель гетероскедастичности (MGARCH) – принадлежат к данной категории и используются для оценки вариационно-ковариационной матрицы в расчёте VaR. В исследованиях, посвященных VaR, MGARCH является наиболее устойчивым и широко используемым эталоном.
MEWMA рекурсивно определяется как
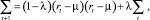
где rt – n×1 вектор доходов; µ – вектор ожидаемых доходов; λ ∈ (0, 1);
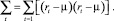
В течение последних десятилетий проводились активные исследования моделей MGARCH с целью моделирования временных рядов [9]. Однако только недавно были предприняты попытки исследовать показатели, основанные на VaR MGARCH. Среди исследователей можно отметить Ромбаутса и Вербека [11]; Ку и Вонга [10]; Хуанга и соавт. [9]. Модель DCC-MGARCH определяется как
rt = α0 + α1 rt + μt + εt+1,
где rt относится к возврату со временем t; rt ~ N(0, Dt+1 RDt+1); µt – N – бесконечномерный вектор условного среднего значения;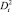 
может быть определен как любая одномерная GARCH модель, т.к.
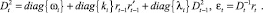
Матрица динамической условной корреляции Rt от εt при времени t определяется следующим образом:
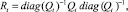
где Qt является N×N симметричной положительно определенной безотносительной матрицей корреляций εt, как в уравнении
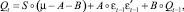
где ° – произведение Адамара двух идентичных по размерам матриц.
Непараметрический подход основывается на исторических данных для выведения устойчивой схемы. Такой подход устанавливает меньше строгих условий, однако присутствует риск чрезмерно близкой подгонки при извлечении данных. К данной категории относятся историческое моделирование методом Монте-Карло, а также подходы нейронных сетей и регрессионного анализа.
Принимая во внимание результаты работы моделей, можно определить будущие результаты, а адекватность модели может быть представлена в количественном отношении на основании результатов проверок с использованием исторических данных.
Если модель применима, число маловероятных потерь х должно следовать двумерному нормальному распределению. Таким образом, при данном общем числе наблюдений n при уровне доверительной вероятности p вероятность расcчитывается следующим образом:
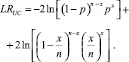
Статистика результатов проверок отношения правдоподобия Купьец согласовывается с распределением χ2.