Современные кризисные явления, наблюдающиеся в экономике страны, актуализируют активное использование рыночных механизмов их преодоления. Одним из таких механизмов традиционно является использование кредитного ресурса для развития и сохранения устойчивого функционирования предприятий. В рыночных условиях кредитный ресурс является платным и влияет на результативность деятельности предприятия. В этой связи актуальной является задача разработки формализованного, автоматизированного инструментария, позволяющего определять объемы и условия целесообразности привлечения кредитного ресурса, а также анализировать соответствующие характеристики производственного проекта для выбора оптимальных значений срока его действия в зависимости от форм его финансирования.
Известно [3–7], что для решения задач планирования деятельности экономических систем целесообразно использовать линейные оптимизационные математические модели, позволяющие выявлять экономический потенциал исследуемых систем, а также разрабатывать эффективный численный инструментарий их анализа. Рассмотрим следующую экономико-математическую модель функционирования экономической системы, описывающей взаимодействие производителя и налогового центра в ней, в форме двухкритериальной задачи линейного программирования:
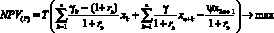 (1)
(1)
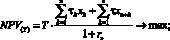 (2)
(2)
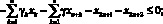 (3)
(3)
–δkxk + xn+k ≤ 0; (4)
xn+k ≤ qk; (5)
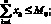 x2n+1 ≤ Cr0; x2n+2 ≤ Dot0; (6)
x2n+1 ≤ Cr0; x2n+2 ≤ Dot0; (6)
xj ≥ 0 (j = 1, ..., 2n + 2), (7)
где
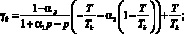
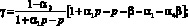
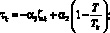
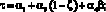
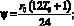
n – количество видов продукции, ед., k = 1, …, n – порядковый номер ОПФ; Т – срок действия (горизонт планирования), r – годовая ставка дисконтирования; xk (k = 1, …, n) – стоимость приобретаемых ОПФ k-го вида за период Т, д.е.; xn+k (k = 1, …, n) – выручка от реализации всей продукции k-го вида за период Т, произведенной на k-м ОПФ, д.е.; x2n+1 – сумма кредита, взятого под обеспечение финансирования проекта; x2n+2 – сумма дотаций предприятию за период Ш; сk – стоимость единицы k-го ОПФ, д.е./ед.ОПФ; Pk – стоимость продажи единицы продукции на k-го вида, д.е./ед. продукции; Tk – время полезного использования k-го ОПФ, лет; Vk – производительность k-го ОПФ за период Т, ед. продукции/(ед. ОПФ); qk – спрос на продукцию, произведенную на k-м ОПФ, за период Т д.е./(ед.прод); 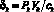 – фондоотдача k-го ОПФ за период Т, %; αi, i = 1, …, 4 – соответственно ставки налогов на добавленную стоимость, имущество, прибыль, страховых взносов в социальные фонды; p – экспертный показатель материалоемкости производства (доля оборотных затрат в сумме всех затрат производителя); β – экспертный показатель трудоемкости производства (доля выручки от продаж, выделяемая в фонд оплаты
– фондоотдача k-го ОПФ за период Т, %; αi, i = 1, …, 4 – соответственно ставки налогов на добавленную стоимость, имущество, прибыль, страховых взносов в социальные фонды; p – экспертный показатель материалоемкости производства (доля оборотных затрат в сумме всех затрат производителя); β – экспертный показатель трудоемкости производства (доля выручки от продаж, выделяемая в фонд оплаты
труда (ФОТ)); M0 – максимальная сумма инвестиций в ОПФ; Cr0 – максимальная сумма кредита; Dot0 – максимальная сумма дотаций; 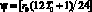 – сумма платежа за кредит по ставке r0 на срок T0;
– сумма платежа за кредит по ставке r0 на срок T0; 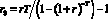 – эффективная ставка дисконтирования проекта за период Т.
– эффективная ставка дисконтирования проекта за период Т.
Охарактеризуем далее содержательный смысл условий модели (1)–(7). Соотношение (1) представляет собой целевой критерий, отражающий, на горизонте Т, дисконтированное сальдо стратегических доходов (прибыль и поток имущества) и стратегических расходов (инвестиции), с учетом составляющей платности заемного финансирования, а (2) – целевой критерий налогового органа при его взаимодействии с производителем. При этом в первом приближении считается, что налоговый орган собирает лишь основные налоги, объем которых пропорционален объему производимой продукции, а также налог на имущество предприятий. Соотношение (3) отражает условие неотрицательности текущих денежных средств производителя на горизонте Т, позволяющее устранить риски его неплатежеспособности. Условия (4) и (5) ограничивают объемы производства продукции в системе либо проектными возможностями основных производственных фондов (производительностью, фондоотдачей, уровнем развития научного технического прогресса и т.п.), либо условиями внешней рыночной среды (платежеспособный спрос на продукцию, определяемый рыночной нишей производителя, долей рынка, уровнем доходов потребителей и т.п.). Условия (6) учитывают ограниченность объемов инвестиционного, кредитного и дотационного ресурсов соответственно, а условия (7) имеют содержательный смысл неотрицательности значений искомых переменных задачи.
Cогласно монографии [10], двухкритериальная ЗЛП (1)–(7) эквивалентна однокритериальной линейной задаче с теми же ограничениями и максимизацией свертки целевых критериев
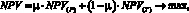
где параметр μ ∈ (0; 1) трактуется как весовой коэффициент значимости критерия NPV(P).
Задача линейного программирования в модели (1)–(7) имеет решение при всех допустимых значениях переменных в силу компактности допустимого множества и принадлежности множеству решений нулевого вектора (X = 0), где Х = (x1,…, xn; xn+1,…, x2n; x2n+1, x2n+2)T – вектор-столбец, содержащий инвестиционную, производственную и финансовую группу искомых переменных. Наличие нетривиальных решений задачи в модели (1)–(7) показано ниже при ее численном анализе с использованием оптимизационного программного продукта «Карма», подробно описанного в работах [1, 9]. Система «Карма» содержит модули занесения и контроля входной информации, графического, многопараметрического и многокритериального анализа задач линейного оптимального управления, а также элементов финансово-хозяйственной деятельности, и тем самым представляет собой систему поддержки принятия решений, ориентированную на оперативный, экспертный анализ экономических проектов широкого круга приложений. Указанный комплекс показал свою эффективность при анализе ряда инвестиционных проектов мезо[2, 4, 5, 8, 9] и микроэкономического уровня [1, 3, 6, 7]. Рассмотрим численный эксперимент по модели (1)–(7) с использованием финансово-аналитического программного продукта [1]. При этом в качестве основных задач эксперимента будем рассматривать выбор оптимальных значений срока действия производственного проекта в зависимости от различных форм его финансирования.
Пусть, например,
n = 1; β = 0,2; µ = 1; p = 0,2; α1 = 0,18;
α2 = 0,02; α3 = 0,2; α4 = 0,3; r = 0,3;
M0 = 80000 тыс. руб.; c1 = 25000 тыс. руб.;
P1 = 20 тыс. руб./т; T1 = 20 лет;
V1 = 5100 т/год; q1 = 10000 тыс. руб./год.
Отметим, что данный набор значений входных параметров модели характеризует некоторый реальный инвестиционный проект по производству, на основе угольного сырья, востребованной рынком продукции.
На рис. 1 приведены графики зависимостей чистой приведенной стоимости NPV(Р) производителя от горизонта планирования Т при варьировании форм его финансирования (дотации (Dot0) и/или кредиты (Cr0)):
1) – Cr0 = Dot0 = 0;
2) – Cr0 = 100, Dot0 = 0;
3) – Cr0 = 0, Dot0 = 100;
4) – Cr0 = 0, Dot0 = 500;
5) – Cr0 = 0, Dot0=5000.
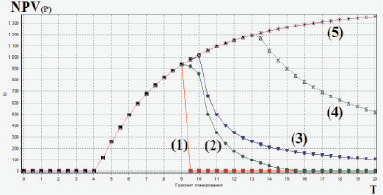
Рис. 1. Зависимости NPV проекта от горизонта планирования и форм финансирования
Как видно из рисунка, без финансирования текущей деятельности (график 1), исследуемый проект имеет оптимальное значение NPV при Т = 9 лет. При наличии заёмного финансирования (Cr0 > 0) (график 2), оптимальный срок действия проекта не меняется, однако в значительной мере изменяется форма графика после достижения оптимума, что можно трактовать как повышение общей устойчивости проекта. Данный факт численно отражается в увеличении срока действия проекта Т ≈ 15 лет, при котором он имеет положительную NPV(Р). Подключение форм безвозмездного финансирования (рост объемов дотаций Dot0) приводит к значительному улучшению характеристик устойчивости проекта (графики 3–5). При значительных объемах безвозмездной финансовой поддержки график принимает характерный вид возрастающей, выпуклой вверх кривой. Из рис. 1, кроме данных для анализа оптимальных сроков действия, можно получить и другую информацию о проекте. В частности, наглядно оцениваются срок окупаемости (приблизительно 4 года), максимальные значения NPV(Р) при варьировании не только выбранных параметров финансирования, но и любого другого параметра из списка приведенных выше.
Проведем следующий численный эксперимент по определению оптимального объема финансирования проекта. При заданных выше характеристиках проекта будем увеличивать значение параметра Cr0 (максимальная сумма кредита) до тех пор, пока сумма значений переменных x2n+1, x2n+2 в задаче (1)–(7) не достигнет максимума. Основной задачей эксперимента будем рассматривать определение таких характеристик проекта, как ставка и срок кредита на обеспечение текущей деятельности.
На рис. 2 приведены зависимости эффективности NPV(Р) проекта от изменения параметра Cr0, а на рис. 3, 4 – зависимости NPV(Р) от ставки и срока кредита соответственно.
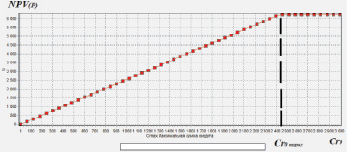
Рис. 2. Зависимость NPV проекта от максимального объема кредита
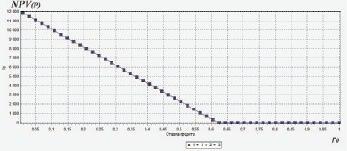
Рис. 3. Зависимости NPV проекта от ставки кредита
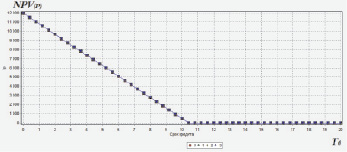
Рис. 4. Зависимость NPV проекта от срока кредита
Из рисунков визуально определяются характеристики проекта, связанные с его заемным финансированием. В частности, рис. 2 иллюстрирует пороговые значения критерия и соответствующего ему параметра Cr0 при заданных исходных параметрах. По рис. 3 и 4 принимающее решения лицо может выбирать целесообразные для него значения ставок и сроков кредита.
Следует отметить, что приведенная на рисунках картина распределений NPV(Р), а также потребность в кредите возникают, как правило, при таких условиях реализации проекта, когда характеристики его эффективности находятся в диапазонах своих рисковых, критических значений. Например, текущие рыночные цены единицы продукции, наблюдавшиеся в реальном проекте, находились в диапазоне P1 = 30–40 тыс. руб./т, что свидетельствовало об эффективности и прибыльности проекта и его возможностях финансирования без привлечения кредитного ресурса. Однако приведенные зависимости реализуются при достаточно пессимистических значениях параметров: P1 = 20 тыс. руб./т и уровне значений NPV(Р), не превышающем 1000 тыс. руб. на каждый год срока действия проекта. Данный факт имеет свое естественное содержательное объяснение, так как именно в случае рисковых вариантов реализации проектов кредитный ресурс играет свою экономическую роль их стабилизатора в смысле увеличения запасов финансовой устойчивости, несмотря на потери результативности.
Таким образом, с помощью модели (1)–(7) и системы поддержки принятия решений [1, 3, 4, 9] нами получены значения оптимальных сроков действия производственного проекта в зависимости от форм его финансирования. При этом численно определены параметры финансирования текущей деятельности и показано, что оно может значительно улучшать характеристики устойчивости производственного проекта в случае критических сценариев его реализации.



