Для современных систем управления одной из наиболее приоритетных задач является обеспечение высоких показателей скорости, надежности и качества передачи управляющей информации [2]. Для этого система должна обладать требуемой помехоустойчивостью, которая характеризует способность системы сохранять заданные количественные и качественные показатели несмотря на наличие помех в канале связи [3]. На сегодняшний день одним из основных способов обеспечения высокой помехоустойчивости является применение избыточных (корректирующих) кодов, которые за счет введения дополнительных символов и процедур обработки сообщений позволяют обнаруживать и исправлять ошибки [5].
В связи с прогрессом в теории и технике кодирования в современных системах передачи информации, в том числе спутниковых системах связи, используются сверточные неблоковые коды [5]. Использование сверточных кодов обусловлено высокой эффективностью – соотношением корректирующей способности и избыточности, превышающей соответствующие показатели аналогичных по размерности блоковых избыточных двоичных кодов (например групповых или циклических) [6–9]. Поэтому исследование сверточных кодов представляется важным и своевременным.
Краткая теория: принципы построения, кодирования и декодирования сверточных кодов
Сверточный код описывается тремя целыми числами [5]: n, k, K , где отношение k/n называется степенью кодирования кода (code rate) и показывает количество информации, приходящейся на закодированный бит. Целое число K является параметром, называемым длиной кодового ограничения; оно указывает на число разрядов кодирующего регистра сдвига. Целое число k указывает на число бит данных, которые образуют вход блочного кодера. Число n – это суммарное количество разрядов в соответствующем кодовом слове на выходе кодера.
Исходное сообщение на входе обозначается последовательностью m = m1, m2, ..., mi, ..., где mi – двоичный бит, а i – индекс времени (расположение элемента внутри последовательности). Будем предполагать, что все mi равновероятны единице или нулю и независимы между собой. Будучи независимой, последовательность битов нуждается в некоторой избыточности, т.е. значение бита mi не дает информацию о бите mj. Кодер преобразует последовательность m в уникальную последовательность кодовых слов U = G(m). Последовательность m однозначно определяет последовательность U. Несмотря на это, ключевой особенностью сверточных кодов является то, что данный k-картеж внутри m не однозначно определяет связанные с ним n-кортежи внутри U. Это объясняется тем, что кодирование каждого k-кортежа является функцией не только k-кортежей, но и предыдущих (K–1) k-кортежей.
Последовательность U можно разделить на последовательность кодовых слов: U = U1, U2, ..., Ui, .... Каждое кодовое слово Ui состоит из двоичных кодовых символов, называемых канальными битами или битами кода; в отличие от битов входного сообщения, кодовые символы не являются независимыми.
Обычный сверточный кодер [5], показанный на рис. 1, реализуется с K-разрядным регистром сдвига и п сумматорами по модулю 2, где K – длина кодового ограничения. Длина кодового ограничения – это количество k-битовых сдвигов, после которых один информационный бит может повлиять на выходной сигнал кодера.
В каждый момент времени на место первых k разрядов регистра перемещаются k новых бит; все биты в регистре смещаются на k разрядов вправо, и выходные данные п сумматоров последовательно дискретизируются, давая в результате биты кода. Поскольку для каждой входной группы из k бит сообщения имеется n бит кода, степень кодирования равна k/n бит сообщения на бит кода, где k < n.
Для реализации сверточного кодирования можно воспользоваться методом решетчатой диаграммы. Решетчатая диаграмма отражает все возможные состояния регистра сдвига и выходные состояния кодера в течение всего числа тактов, требуемых для передачи входной последовательности. Решетчатая диаграмма для сверточного кодера показана на рис. 2.
Принцип построения диаграммы основан на том, что в каждый ti момент времени в регистр сдвига входит бит – 0 или 1, изменяя состояние регистра. По состоянию регистра уже вычисляется кодовое слово, и на основе этих данных строится решетчатая диаграмма.
Декодирование сверточных кодов выполняется методом построения решетчатой диаграммы на основе данных решетчатой диаграммы кодера. Для решетки декодера каждую ветвь за каждый временной интервал удобно пометить расстоянием Хэмминга между полученным кодовым словом и кодовым словом, соответствующим той же ветви из решетки кодера. Пометки на решетке декодера накапливаются декодером в процессе. Другими словами, когда получен кодовый символ, каждая ветвь решетки декодера помечается метрикой подобия, между полученным кодовым символом и каждым словом ветви за этот временной интервал. В каждый момент времени ti в решетке существует 2K–1 состояний, где K – длина кодового ограничения, и в каждое состояние может войти несколько путей. Решетчатая диаграмма сверточного декодера изображена на рис. 3.
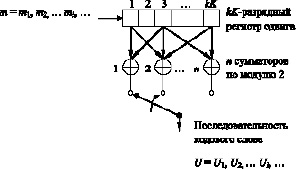
Рис. 1. Сверточный кодер
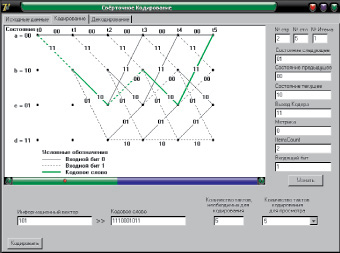
Рис. 2. Решетчатая диаграмма кодера (K = 3, k = 1, g1(x) = 1 ⊕ x2, g2(x) = 1 ⊕ x)
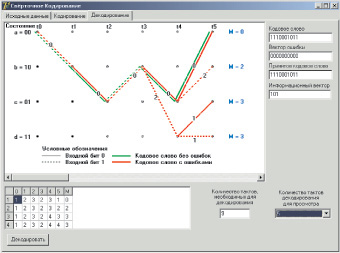
Рис. 3. Решетчатая диаграмма работы сверточного декодера
Наибольшую популярность получил алгоритм декодирования Витерби. Принцип декодирования основан на сравнении метрик путей, входящих в каждое состояние, и исключении всех, кроме пути с минимальной метрикой. Таким образом, в каждый момент времени на решетчатой диаграмме получается не больше 2K–1 возможных путей для правильного декодирования последовательности. После исключения для каждого момента времени ti анализируются все предыдущие моменты времени декодирования для 0 ≤ j < i. Если на интервале tj–1...tj остается только один путь, то соответствующий ему символ и считается правильно декодированным. В зависимости от кратности и распределения ошибок декодирования может осуществляться количество тактов, в несколько раз превышающее количество принятых символов, т.е. с временной задержкой. Корректирующая способность кода (исправление ошибок) связана с длиной кодового ограничения (по аналогии с шириной сигнальной зоны – для блоковых кодов).
Разработка и исследование модели системы управления, в которой используется сверточное кодирование данных
Изучение вопросов построения и реализации сверточных кодов предлагается осуществить в рамках лабораторного практикума. Для этого разработан и подготовлен виртуальный лабораторный стенд, реализованный в двух вариантах. Программная модель (рис. 2, 3), разработанная в среде объектно-ориентированного программирования Borland Delphi 7.0, позволяет изучить и промоделировать работу процедур кодирования и декодирования, корректирующие свойства кода с заданными параметрами. Программная модель системы управления (рис. 4, а), реализованная в среде MathWork MatLab [10], пакете Simulink, позволяет исследовать корректирующие свойства кода, задавая в модели канала связи ошибки разной конфигурации (рис. 4, б) и параметры кодирующих и декодирующих устройств (рис. 4, в).
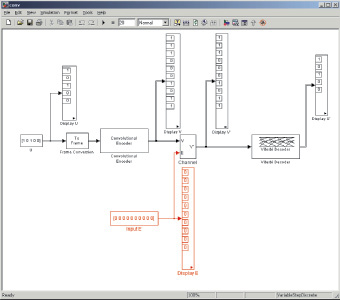
а
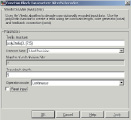
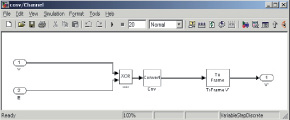
б в
Рис. 4. Модель системы управления в пакете Simulink
Исследование традиционно состоит из двух частей: расчетной и исследовательской. В расчетной части необходимо выполнить расчет параметров сверточного кода по заданным исходным данным, промоделировать работу кодирующего устройства, построить решетчатую диаграмму и по ней промоделировать работу кодера и декодера в режиме исправления ошибок различного местоположения и кратности. В качестве исходных данных указываются: длина информационной части n, длина кодового ограничения K, количество бит k, которые образуют вход блочного кодера, полиномиальные генераторы g(x), варианты полинома ошибок e(x).
В исследовательской части необходимо исследовать все возможности сверточных кодов с помощью модели системы управления, используя результаты расчетной части. Для этого им необходимо будет ввести характеристики кода (количество связей кодера, количество входных бит данных, количество разрядов кодирующего регистра сдвига). Согласно этим характеристикам кода студенты с помощью программы моделируют работу кодирующего и декодирующего устройств, проверяют достоверность переданных последовательностей и принимают решения об эффективности сверточного кодирования.
Заключение
Целью статьи является рассмотрение вопросов разработки комплекса исследовательских работ, направленных на изучение современных методов помехоустойчивого кодирования информации, что важно для профессиональной подготовки специалистов в области систем управления [1, 4]. Был произведен аналитический обзор кодирования и декодирования избыточных сверточных кодов, рассмотрены процедуры кодирования и декодирования. Также показаны основные подходы к организации лабораторной работы с использованием виртуального лабораторного стенда, построенного в среде объектно-ориентированного программирования Borland Delphi 7.0 и MathWorks Matlab.



