В настоящее время большинство крупных предприятий, таких как ПАО НК «Роснефть», ПАО «Газпром», ПАО «ИНТЕР РАО ЕЭС» и др., имеют значительные наработки в формализации и стандартизации бизнес-процессов на базе методологии ARIS [7].
В ряде публикаций, например в [3, 5, 8], предлагается проводить анализ бизнес-процессов, представленных в нотации ARIS eEPC, с использованием аппарата сетей Петри.
Стоит подчеркнуть, что в указанных публикациях не рассмотрено решение существенных для анализа бизнес-процессов и оценки рисков в них классических задач для сетей Петри, таких как задача достижимости маркировки и задача покрываемости маркировки.
В настоящей статье для анализа нечетких бизнес-процессов и оценки рисков предлагаются способы, основанные на интерпретации нечетких бизнес-процессов с помощью аппарата высокоуровневых нечетких сетей Петри [5], решении задачи покрываемости маркировки с построением совокупности маршрутов и расчетом искомых характеристик исследуемого состояния сети с использованием нечеткой продукционной модели (на примере модели Сугэно 0-го порядка).
Интерпретация бизнес-процесса, представленного в нотации ARIS eEPC, в виде сети Петри
Основными элементами бизнес-процессов [5] являются:
- F = {f1...fh} – множество функций ARIS eEPC, где h – количество функций в бизнес-процессе;
- E = {e1...er} – множество событий ARIS eEPC, где r – количество событий в бизнес-процессе;
- P = {p1...pc} – множество организационных единиц ARIS eEPC, где c – количество организационных единиц в бизнес-процессе;
- D = {d1...dv} – множество документов ARIS eEPC, где v – количество документов в бизнес-процессе;
- S = {s1...sz} – множество прикладных систем ARIS eEPC, где z – количество прикладных систем в бизнес-процессе;
- K = {k1...ky} – множество кластеров информации ARIS eEPC, где y – количество кластеров информации в бизнес-процессе.
Совместно множества P, D, S, K обозначим в виде множества R – ресурсов бизнес-процесса. Таким образом, модель бизнес-процесса, представленного в нотации ARIS eEPC, является 3-дольным графом. Для установления связей между элементами, вводятся следующие матрицы переходов [7]:
- EF – матрица размерности r×h, отражающая связи между событиями и вызываемыми ими функциями;
- FE – матрица размерности h×r, отражающая связи между функциями и порождаемыми ими событиями;
- RF – матрица размерности (c + v + z + y)×h, отражающая связи ресурсов с функцией, в которую они передаются;
- FR – матрица размерности h×(c + v + z + y), отражающая связи функции с порождаемыми ей ресурсами.
Таким образом, бизнес-процесс может быть задан кортежем:
BP = ⟨F, E, P, D, S, K, EF, FE, RF, FR⟩.
Для моделирования бизнес-процессов в [10] предложено использовать формализм нечетких высокоуровневых сетей Петри (HLFPN) [9]. Между формальным описанием бизнес-процесса в нотации ARIS eEPC и HLFPN устанавливается следующее соответствие:
- множество функций F соответствует множеству переходов T HLFPN – F - T;
- множество атрибутов событий и ресурсов ARIS eEPC E, P, D, S, K ставится в соответствие множеству позиций P HLFPN –
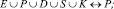
- множества переходов ARIS eEPC EF, FE, RF, FR ставятся в соответствие с набором направленных дуг F HLFPN –
.
Перед моделированием осуществляется наполнение HLFPN знаниями.
Шаг 1. Проводится извлечение информации об обстоятельствах протекания бизнес-процессов (атрибутах ресурсов бизнес-процессов) и их результатах (атрибутах выходных ресурсов каждой функции) из экспертов и/или баз данных. Эта выборка станет обучающей выборкой для каскада продукционных моделей, представленных HLFPN.
Шаг 2. Для всех атрибутов всех ресурсов с привлечением экспертов формируются функции принадлежности (membership functions).
Шаг 3. Набор нечетких продукционных правил образуется путем полного комбинаторного перебора всех возможных комбинаций всех термов всех атрибутов всех ресурсов, поступающих на вход перехода.
Следует учитывать, что ряд атрибутов ресурсов может одновременно являться и входными и выходными для нечеткой продукционной модели. Так, например, при выполнении функции бизнес-процесса может изменяться эмоциональное состояние исполнителя как в лучшую сторону (получение удовлетворенности от работы), так и в худшую сторону (угнетение от выполнения работы с некачественными исходными данными, документами и т.д.).
Шаг 4. Проводится обучение каждой отдельной нечеткой продукционной модели.
Рассмотрим обучение на примере продукционной модели Сугэно 0-го порядка, в которой консеквент каждого из нечетких продукционных правил является константой. Такая модель может быть достаточно быстро обучена на нескольких примерах с использованием, например, метода генетического алгоритма, как показано в [4], или на основании градиентного метода (см., например, [2]).
Построение маршрута бизнес-процесса в терминах сетей Петри
Для выполнения анализа бизнес-процессов одной из основных задач является задача построения маршрута между начальным и конечным событиями с целью определения возможности достижимости требуемого результата или совокупности результатов. С учетом предлагаемого в настоящей статье подхода к формализации бизнес-процессов в терминах сетей Петри задачу построения маршрута бизнес-процесса можно переформулировать в виде задачи покрываемости маркировки сети Петри [6].
При реализации алгоритма используются следующие входные данные:
– сеть Петри, заданная орграфом;
– начальная и конечная позиции сети Петри.
В результате функционирования предлагаемого алгоритма по входным данным формируется структура, содержащая упорядоченную (по идентификаторам вершин) совокупность маршрутов, связывающих фиксированную начальную вершину-позицию с остальными вершинами-позициями сети Петри, после чего осуществляется выборка маршрутов по идентификатору конечной вершины.
Основные обозначения
1. Пусть P – множество вершин-позиций сети Петри, T – множество вершин-переходов,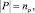 
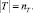
2. Маршрут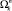 
между вершинами-позициями PS и Pn представляет собой классический однонаправленный список вершин:
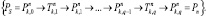
3. Под длиной пути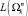 
будем понимать количество переходов в списке 
.
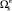4. Под ресурсным весом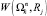 
маршрута 
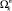будем понимать суммарное количество ресурса Rj, потребляемого системой при осуществлении всех переходов 
.
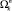5. Под условным фактором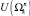 
будем подразумевать совокупное множество условий, необходимых для осуществления всех переходов 
.
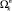6. Под условностью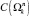 
маршрута будем понимать мощность множества 
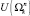. Если 
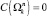, то маршрут 
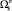будем называть безусловным.
7. Под пространством маршрутов будем подразумевать одномерный массив Ω длины np, n-й элемент которого представляет собой множество маршрутов Ωn с началом в вершине PS и окончанием в вершине Pn.
В таком случае способ построения маршрута можно описать следующим набором шагов.
1. Формируем массив Ω длины np, описанный в пункте 7 «основных обозначений». Формируем очередь Q для размещения пар (n; k), где n – номер вершины-позиции, а k – номер маршрута до этой вершины от вершины PS.
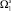присваиваем значение {PS} (путь нулевой длины). Помещаем в очередь пару (s; 1).
2. Пока Q ≠ Ø:
2.1. Извлекаем очередной элемент (n; k) из очереди Q.
2.2. Рассматриваем все возможные переходы из позиции Pn. Для определенности пусть позиция Pm достижима из Pn через переход Tj. Если ни один из маршрутов Ωm не содержит в качестве субсписка маршрут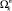 
:
2.2.1. Копируем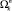 
в Ω+ .
2.2.2. Добавляем в конец списка Ω+ Tj и Pm.
2.2.3. Ωm = Ωm + {Ω+}.
2.2.4. Помещаем пару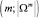 
в очередь Q.
3. Множество всех маршрутов от вершины PS до вершины PF определяется как ΩF. Если ΩF = Ø, маршрут между PS и PF не существует. В противном случае переходим к пункту 4.
4. Удаляем из ΩF все маршруты, для которых хотя бы одно из условий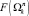 
не может быть выполнено. Если ΩF = Ø, маршрут между PS и PF не существует. В противном случае переходим к пункту 5.
5. В случае необходимости определения оптимального маршрута между PS и PF выполняем многокритериальную сортировку маршрутов ΩF с учетом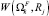 
, 
, 
.
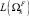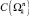Таким образом, в результате работы алгоритма формируется структура, содержащая все ациклические маршруты, связывающие вершину PS с остальными вершинами-позициями сети Петри, после чего определяется возможность покрываемости позиции PF из вершины PS и формируется список всех маршрутов до этой позиции.
Способы анализа нечетких бизнес-процессов
Анализ нечетких бизнес-процессов заключается в оценке качества искомых результатов бизнес-процесса. Сами результаты при этом могут не достигаться в рамках одного запуска бизнес-процесса. Поэтому можно предложить семейство способов анализа нечетких бизнес-процессов, отличающихся набором одновременно получаемых результатов:
1) способ анализа нечетких бизнес-процессов, при одновременном получении всех заявленных результатов;
2) способ анализа нечетких бизнес-процессов, при получении раздельных результатов.
Способ анализа нечетких бизнес-процессов, при одновременном получении всех заявленных результатов
Предполагается, что перед началом анализа бизнес-процесс интерпретирован в высокоуровневую сеть Петри, в которой каждой искомой характеристике сопоставлена вершина сети Петри. Нечеткая высокоуровневая сеть Петри обучена. При соблюдении обозначенных условий способ будет включать следующие шаги.
1. С использованием алгоритма построения маршрутов бизнес-процесса, изложенного в разделе 2, для каждого искомого атрибута, формируется совокупность маршрутов сети Петри, связывающих начальную и конечную вершины-позиции сети Петри (конечная позиция сети Петри соответствует возникновению события бизнес-процесса, связанного с формированием конечного требуемого документа).
2. Осуществляется анализ маршрутов полученных маршрутов с целью нахождения общих из них.
3. В случае, если общие маршруты найдены, то для каждого из них осуществляется моделирование нечеткого бизнес-процесса по правилам нечеткой высокоуровневой сети Петри.
4. Осуществляется агрегирование значений каждой искомой характеристики по общим маршрутам с использованием, например, операций T- и S-норм [1].
5. Полученные на шаге 4 обобщенные оценки совместно с результатами оценки искомых характеристик по каждому из общих маршрутов принимаются к рассмотрению.
6. При наличии определенных критериев рисков осуществляется отсев маршрутов, которые приводят к неудовлетворительным значениям рисков. Оставшиеся маршруты развития бизнес-процесса считаются предпочтительными.
7. Оптимальный в некотором смысле маршрут бизнес-процесса может быть получен исходя из оценки маршрутов по следующим показателям: длина пути (количество переходов), объем используемых ресурсов. При этом, при дополнении сети до временной сети Петри, длина пути также может измеряться временем выполнения процесса.
Способ анализа нечетких бизнес-процессов, при получении раздельных результатов
Как и в предыдущем способе, предполагается наличие соответствующим образом обученной нечеткой высокоуровневой сети Петри, отражающей бизнес-процесс. В таком случае способ включает следующие шаги:
1. С использованием алгоритма построения маршрутов бизнес-процесса, изложенного в разделе 2, для каждого искомого атрибута, формируется совокупность маршрутов сети Петри, связывающих начальную и конечную вершины-позиции сети Петри (конечная позиция сети Петри соответствует возникновению события бизнес-процесса, связанного с формированием конечного требуемого документа).
2. Осуществляется анализ маршрутов полученных маршрутов с целью нахождения общих из них.
3. Для всех маршрутов осуществляется моделирование нечеткой высокоуровневой сети Петри. Полученные результаты принимаются к рассмотрению.
4. Определяются критерии выбора оптимальных в некотором смысле маршрутов. Результаты бизнес-процесса делятся на обязательные и факультативные. Для каждого обязательного результата критерий его удовлетворительности.
5. Осуществляется отсев маршрутов, не обеспечивающих получение обязательных результатов, удовлетворяющих критериям.
6. В случае, если после шага 5 не остается ни одного маршрута, осуществляется поиск маршрута, обеспечивающего получение максимального количества обязательных результатов.
7. В случае, если после шага 5 остается несколько маршрутов, с использованием, например, модели предпочтений экспертов, на основании характеристик обязательных и факультативных результатов, осуществляется ранжирование полученных маршрутов. В модели предпочтений экспертов также могут учитываться длина маршрута (количество переходов) и объем используемых ресурсов.
Полученные с использованием приведенных способов маршруты могут использоваться в дальнейшем для регулирования бизнес-процесса (направления его по нужному маршруту).
Заключение
Таким образом, предложенные способы, применяемые в зависимости от потребности, обеспечивают анализ нечетких бизнес-процессов для управления рисками и позволяют лицу, принимающему решения, своевременно влиять на ход бизнес-процесса с целью достижения результата, удовлетворяющего заданным критериям.
Работа выполнена при поддержке Совета по грантам Президента РФ в рамках научного проекта МК-6184.2016.8.