В настоящее время низкоорбитальные системы спутниковой связи применяются в комплексах дистанционного контроля, мониторинга и управления необслуживаемыми объектами добычи и транспортировки углеводородов, расположенных на Крайнем Севере. С целью предотвращения навязывания активной имитационной помехи чужим спутником-нарушителем предлагается использовать запросно-ответные системы распознавания спутника (ЗОСРС). В работе [1] представлен способ построения ЗОСРС, который применяет протокол аутентификации типа «запрос-ответ», использующий доказательство с нулевым разглашением знаний. Так как все вычислительные операции проводятся по большому модулю, чтобы обеспечить высокую имитостойкость протокола, то запросно-ответная система распознавания спутника характеризуется значительными схемными затратами. Это негативно влияет на надежность работы ЗОСРС. Решить данную проблему можно за счет применения модулярных кодов (МК). Поэтому разработка новых принципов построения запросно-ответной системы распознавания спутника в модулярном коде является актуальной задачей.
Цель исследования
Использование модулярных кодов позволяет повысить точность и скорость выполнения операций сложения, вычитания и умножения по модулю [2, 3]. Переход к параллельной и независимой обработке данных, отсутствие обмена промежуточных результатов вычислений между основаниями МК служит основой для применения таких кодов в процедурах поиска и коррекции ошибок. В отличие от известных помехоустойчивых кодов модулярные коды могут исправлять ошибки, которые возникают в процессе выполнения арифметических операций, тем самым повышая надежность работы вычислительных устройств. Поэтому целью работы является повышение надежности запросно-ответных системы за счет использования разработанного алгоритма поиска и коррекции ошибок с помощью модулярных кодов.
Материалы и методы исследования
С целью повышения надежности запросно-ответной системы опознавания статуса спутника, способ построения которой представлен в работах [1, 4–6], предлагается использовать МК, в частности коды системы остаточных классов (СОК). Коды СОК относятся к непозиционным кодам, в которых число Х представляется в виде кортежа остатков 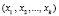 , где
, где 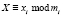 ; i = 1,2,…, k. Взаимно простые числа mi являются основаниями кода СОК. Их произведение определяет рабочий диапазон СОК
; i = 1,2,…, k. Взаимно простые числа mi являются основаниями кода СОК. Их произведение определяет рабочий диапазон СОК
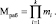 (1)
(1)
Числа 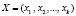 и
и 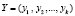 , которые представлены в коде СОК, можно быстро и параллельно складывать, вычитать и умножать по модулям mi. Тогда справедливо
, которые представлены в коде СОК, можно быстро и параллельно складывать, вычитать и умножать по модулям mi. Тогда справедливо
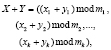 (2)
(2)
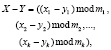 (3)
(3)
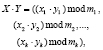 (4)
(4)
где 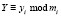 ; i = 1,2,…, k.
; i = 1,2,…, k.
Для разработки новых принципов построения запросно-ответной системы распознавания спутника в модулярном коде необходимо выбрать основания МК, которые бы имели одинаковый первообразный элемент g и удовлетворили условию
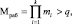 (5)
(5)
где q – модуль, используемый в работе ЗОСРС; g – первообразный элемент мультипликативной группы, порожденной простым числом q.
Воспользуемся алгоритмом работы ЗОСРС, приведенным в работе [1]. Для повышения имитостойкости ЗОСРС в системе кроме секретного ключа U используется сеансовый ключ S(j), а также параметр T(j), который позволяет определить повторное применение сеансового ключа. Представим их в модулярном коде. Тогда
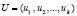 ;
;
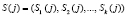 ;
;
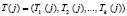 , (6)
, (6)
где
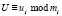 ;
; 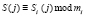 ;
;
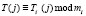 ; i = 1, 2,…, k.
; i = 1, 2,…, k.
На первом этапе ответчик определяет истинный статус спутника с использованием МК
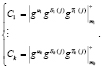 (7)
(7)
На втором этапе ответчик производит зашумление модулярного кода согласно
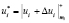 ;
;
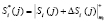 ;
;
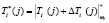 . (8)
. (8)
где
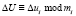 ;
; 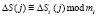 ;
;
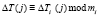 ; i = 1, 2,…, k.
; i = 1, 2,…, k.
На третьем этапе ответчик определяет зашумленный статус спутника в МК
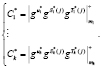 (9)
(9)
На четвертом этапе запросчик пересылает вопрос d = (d1, d2,…, dk) ответчику.
На пятом этапе ответчик приступает к вычислению ответов на вопрос d, согласно
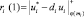 ;
;
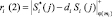 ;
;
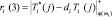 . (10)
. (10)
На шестом этапе ответчик передает запросчику сигнал в виде
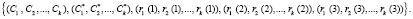
На седьмом этапе запросчик проверяет истинность полученных ответов
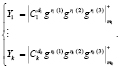 (11)
(11)
Спутник будет считаться «своим», если будет справедливо равенство
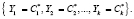 (12)
(12)
Чтобы выполнять поиск и исправление ошибок, необходимо в модулярный код ввести избыточные основания [5, 7, 8]. Для исправления однократной ошибки вводятся два основания mk+1, mk+2, которые удовлетворяют условию
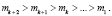 (13)
(13)
Это приводит к появлению полного диапазона МК
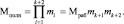 (14)
(14)
Если кодовая комбинация МК не превышает значения Мраб, то такая комбинация не содержит ошибки. В противном случае – комбинация является запрещенной. Чтобы определить данное условие в МК используют позиционные характеристики (ПК) [2, 6, 7, 9]. В работе предлагается разработанный алгоритм вычисления интервальный номер числа. Известно
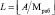 , (15)
, (15)
где  – целая частного, полученного от деления.
– целая частного, полученного от деления.
В алгоритме используется китайская теорема об остатках (КТО), согласно которой
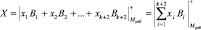 , (16)
, (16)
где Bi – ортогональный базис основания mi.
Для вычисления L воспользуемся свойством подобия ортогональных базисов
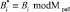 , (17)
, (17)
где Bi, 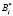 – ортогональные базисы полной и безызбыточной системы оснований.
– ортогональные базисы полной и безызбыточной системы оснований.
Тогда ортогональный базис Bi представляется как
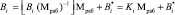 . (18)
. (18)
Известно, что значения интервала числа L крутятся по модулю 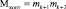 . Значит, выражение (15) можно заменить следующим равенством
. Значит, выражение (15) можно заменить следующим равенством
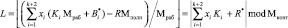 , (19)
, (19)
где 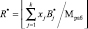 – ранг системы безызбыточного МК.
– ранг системы безызбыточного МК.
Если комбинация не имеет ошибки, то 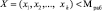 и значение L = 0. В противном случае, при наличии ошибки,
и значение L = 0. В противном случае, при наличии ошибки, 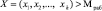 и L > 0. По величине интервального номера можно определить местоположение и глубину ошибки.
и L > 0. По величине интервального номера можно определить местоположение и глубину ошибки.
Результаты исследования и их обсуждение
Пусть заданы основания МК р1 = 11, р2 = 13, р3 = 19, которые обладают g = 2. Диапазон МК будет составлять Мраб = 2717. Выбираем значение секретных параметров и представляем их в СОК: U = 15 = (4, 2, 15), S = 7 = (7, 7, 7), T = 5 = (5, 5, 5). Вычислим истинный статус спутника:
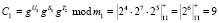 ;
;
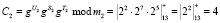 ;
;
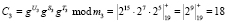 .
.
Значение С = (9, 4, 18) записывается в память КА.
Пусть «зашумление» равно ΔU = 3, ΔS = 5, ΔT = 9. Тогда получаем зашумленные значения U* = (7, 5, 18), S* = (1, 12, 12) и Т* = (3, 1, 14). Вычислим зашумленный статус спутника
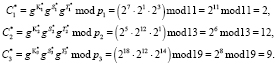
Зашумленный статус спутника равен С* = (2, 12, 9). Он записывается в память КА.
Запросчик, увидев спутник, пересылает ему «вопрос» d = 7 = (7, 7, 7). Ответчик вычисляет ответы на поставленный вопрос. Первый ответ в коде СОК равен
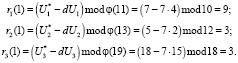
Второй ответ на поставленный вопрос, представленный в коде СОК, имеет вид
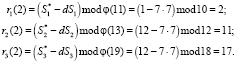
Третий ответ на поставленный вопрос, представленный в коде СОК, имеет вид
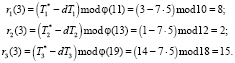
Вычисленные истинный и зашумленный статусы, а также ответы передаются ответчику. Ответчик проверяет статус спутника. Для этого вычисляется
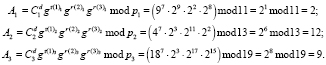
Так как 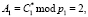
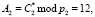
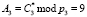 , то спутник аутентифицируется как «свой», и начинается обмен данными между КА и объектом.
, то спутник аутентифицируется как «свой», и начинается обмен данными между КА и объектом.
Рассмотрим выполнение разработанного поиска и коррекции ошибок. Пусть заданы рабочие основания р1 = 11, р2 = 13, р3 = 19. Тогда рабочий диапазон модулярного кода составит Мраб = 2717. В качестве контрольных оснований выбираем р4 = 29, р2 = 37. Это приводит к расширению диапазона М = 2915341. При этом Мконт = 1073. Ортогональные базисы равны
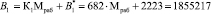 ;
;
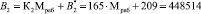 ;
;
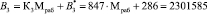 ;
;
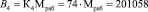 ;
;
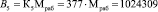 .
.
Пусть на вход устройства поступает разрешенная комбинация А = 401 = (5, 11, 2, 24, 31). Вычислим значение ранга безызбыточного МК по основаниям р1 = 11, р2 = 13, р3 = 19.
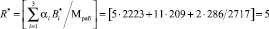 .
.
Воспользуемся алгоритмом (19) для вычисления интервального номера числа
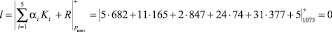 .
.
Так как интервальный номер равен нулю, то это означает, что кодовая комбинация числа А = 401 = (5, 11, 2, 24, 31) является разрешенной и не содержит ошибки.
Пусть в процессе вычислений произошла ошибка, которая исказила первый остаток. Тогда комбинация имеет вид А* = (7, 11, 2, 24, 31). Тогда значение ранга безызбыточного модулярного кода по основаниям
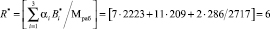 .
.
Вычислим значение интервального номера А* = (7,11,2, 24, 31), используя (19). Получаем
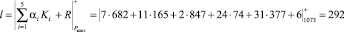 .
.
Так как L = 292, то комбинация числа А* = (7, 11, 2, 24, 31) содержит ошибку. Данное значение интервала соответствует вектору ошибки Δкорр = (9, 0, 0). Исправим ошибку
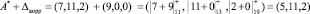 .
.
Заключение
В статье представлены новые принципы построения запросно-ответной системы распознавания спутника в модулярном коде. Так как скорость выполнения мультипликативных операций пропорциональна разрядности операндов, то применение 5-разрядных оснований в рассмотренном примере позволило повысить скорость вычислений более чем в 2 раза, по сравнению с использованием 12-разрядного модуля q. Кроме того применение МК повышает отказоустойчивость запросно-ответной системы распознавания спутника. Разработанный алгоритм вычисления ПХ интервальный номер позволяет исправлять 100 % однократных ошибок, которые возникают в процессе работы ЗОСРС. Данное направление является перспективой применения модулярных кодов для построения отказоустойчивых запросно-ответных систем распознавания спутника.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 17-37-50017.



