1. Рассматривается задача о влиянии вращения Земли на падение тяжелой материальной точки в Северном полушарии, известная еще как задача об отклонении падающих тел на восток [1-4]. Движение точки определяется относительно неинерциальной системы отсчета Оxyz , скрепленной с вращающейся Землей. Начало координат в общем случае располагается на некоторой высоте над сферической поверхностью Земли.
Ось Oz направлена по отвесу вниз, ось Оx - в плоскости меридиана к северу, ось Оy -по параллели к востоку (рис. 1).
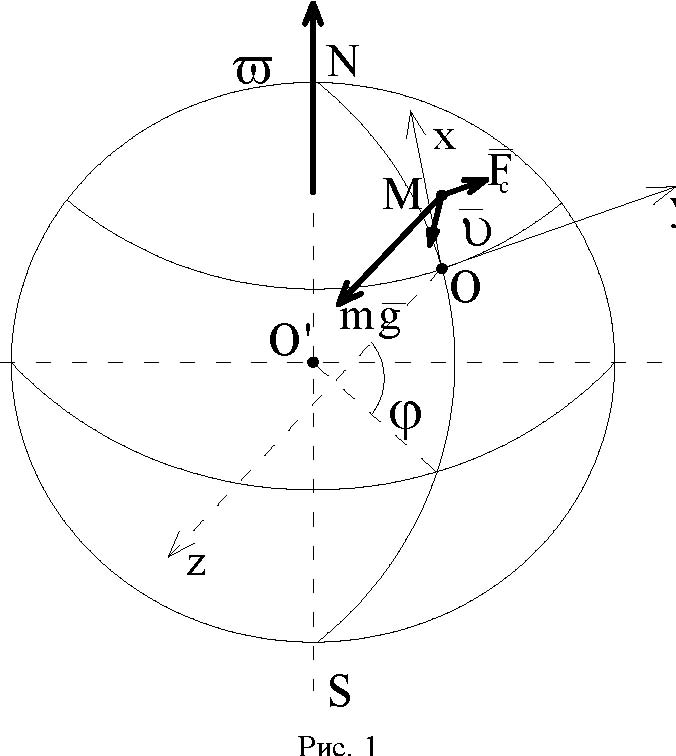
При движении материальной точки вблизи поверхности Земли на нее действуют сила тяготения, переносная и кориолисова силы инерции. Сопротивление воздуха не учитывается. Заменяя сумму силы тяготения и переносной силы инерции силой тяжести 
, а кориолисову силу инерции 
формулой
(1)
Здесь m, 
и 
- соответственно масса, скорость и ускорение точки M, 
- вектор угловой скорости Земли, 
- ускорение силы тяжести.
Отметим, что скорость свободно падающей точки M, начинающей движении из состояния относительного покоя, почти параллельна отвесной линии. Поэтому корио-лисова сила инерции практически перпендикулярна плоскости меридиана и направлена на восток.
Проецируя (1) на координатные оси и следуя [1], получим систему обыкновенных дифференциальных уравнений 2-го порядка
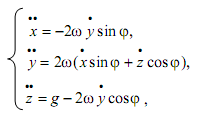(2)
где точки над x, y, z означают их производные по времени, φ - географическая широта места, т.е. угол отвесной линии с плоскостью экватора. Начальные условия следующие:
т.е. в начальный момент времени точка находится в относительном покое. В курсах теоретической механики обычно приводится приближенное решение задачи о влиянии вращения Земли на падение материальной точки без начальной скорости [1-3]. В книге академика Н.А. Кильчевского [4] дано точное решение системы уравнений, с точностью до знаков совпадающей с (2), при нулевых начальных условиях (3). В данной работе получено точное решение системы (2) при ненулевых начальных условиях (см. п. 4.). Предварительно решается задача (2) - (3) (см. п. 2.).
2. Интегрируя каждое из уравнений системы (2), находим
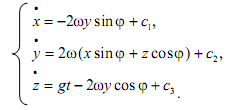
С учетом (3) получаем значения постоянных интегрирования: c 1 = c2 = c3 = 0.
Тогда
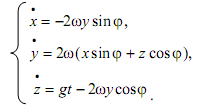
Выражая из (4) 
через y и подставляя во второе уравнение системы (2), имеем
(5)
Дифференциальное уравнение (5) является линейным неоднородным. Следовательно, его решение
y = 
+ Y,
где - общее решение однородного уравнения, Y - частное решение неоднородного уравнения [5]. Корни характеристического уравнения
чисто мнимые 
Поэтому общее решение однородного уравнения
зависящее от двух постоянных интегрирования 
, можно записать в виде
Частное решение
Y=Аt+В, (6)
где А и В неопределенные коэффициенты. Подставляя правую часть (6) в (5)
с учетом 
получим
Сокращая на 2ω и приравнивая друг к другу коэффициенты при первых степенях t и свободные члены, находим
Таким образом, 
а общее решение есть
Удовлетворяя начальному условию y0 = 0, получаем c1* = 0. Условие 
дает
Следовательно,
(7)
Следует заметить, что в [4] выражение для y содержит опечатку - во втором слагаемом коэффициент в знаменателе при ω2 равен единице.
Подставляя правую часть (7) вместо у в первое и третье уравнения системы (4), интегрируя и удовлетворяя начальным условиям x0 = z0 = 0, получим
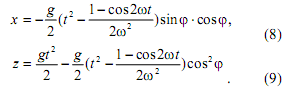
Ввиду того, что ориентация осей x и z противоположна принятой в [4], формулы (8)-(9) отличаются знаками от соответствующих формул, выведенных Н.А. Кильчевским.
Вычитая из (9) выражение (8) при 
будем иметь
Дифференцируя по времени получим
(10)
Опираясь на (8) легко доказать, что для движущейся точки 
Поэтому справедливо неравенство
(11)
Следовательно, при учете кориолисовой силы инерции вертикальная скорость падения точки меньше, чем без ее учета. Иначе говоря, неучет вращения Земли завышает вертикальную скорость падения точки по сравнению с действительной скоростью в пустоте. Этот вывод, представляющий только теоретический интерес, справедлив для всех φ из интервала 
Например, разница в расстояниях, пройденных точкой за 10с падения без учета и с учетом вращения Земли на широте φ=450 не превышает 5 • 10-5м , т.е. величина пренебрежимо малая.
3. Запишем решение задачи (2)-(3) в виде сходящихся рядов. Воспользуемся разложения
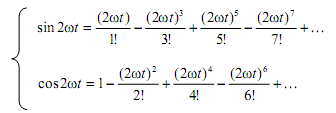
Подставляя правые части этих формул в (7)-(9), после преобразований получим
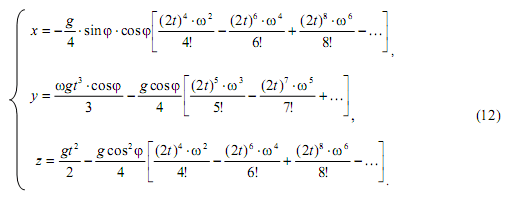
Полагая в (12) ω=0, имеем х=у=0, 
Этот же результат можно получить из (7)-(9) при ω→0.
4. Будем теперь считать, что в начальный момент времени точка M0(x0, y0, z0) имеет относительную скорость 
, отличную от нуля, т.е. рассмотрим систему (2) при следующих начальных условиях:
,
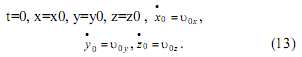Решение задачи (2), (13) можно получить способом, подробно изложенным в п. 2. В случае ненулевых начальных условий выкладки более громоздки, поэтому здесь они опускаются. Решение имеет вид
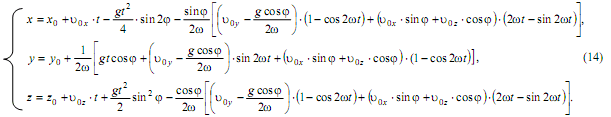
Подстановка в (2) соответствующих производных, полученных из (14) показывает, что каждое из уравнений системы обращается в тождество. Точно выполняются также начальные условия (13). Предполагается, что существует единственное решение задачи Коши для системы (2). Строго говоря, решение (14) должно хорошо согласовываться с опытными данными лишь в такой окрестности начальной точки M 0( x 0,y 0,z 0) , где значения географической широты и ускорения силы тяжести мало отличаются от таковых в этой начальной точке. Чтобы расширить область решения, можно организовать зависящую от времени итерационную пошаговую процедуру, внося в (14) на очередном временнóм шаге поправки, учитывающие изменения φ, g и принимая за начальные условия соответствующие величины, рассчитанные на предыдущем шаге.
Нетрудно видеть, что при 
из (14) следуют равенства (7) - (9). Устремляя ω к нулю (ω →0), из (14) можно получить решение задачи при ненулевых начальных условиях без учета вращения Земли:
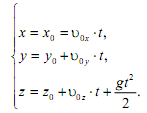
В этом случае траекторией точки является плоская кривая - парабола, поэтому обычно достаточно двух уравнений.
5. Рассмотрим еще шесть вариантов задания начальных условий, во всех из них для простоты полагаем x0 = y0 = z0 = 0.
Вариант I. Пусть 
, т.е. начальная скорость направлена на восток. Тогда кориолисова сила инерции, действующая на точку в начальный момент времени, лежит в плоскости параллели и направлена от оси вращения Земли. Из (14), следуя подходу п. 3., оставляя явно только несколько первых членов рядов, получим
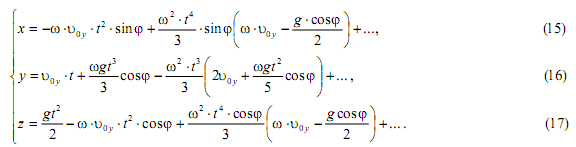
Точка отклоняется на восток и на юг (юго - восток).Формула (15) показывает, что отклонение траектории точки на юг пропорционально первой степени угловой скорости ω. Например, при 
t = 10c оно равно примерно 5 см. В отсутствии начальной скорости отклонение траектории точки на юг вследствие вращения Земли пропорционально квадрату угловой скорости. Этот известный результат следует из формулы для х системы (12).
Вариант II. Пусть 
, т.е. начальная скорость точки направлена на север, следовательно, кориолисова сила инерции, действующая на материальную точку при t=0, направлена на восток. Проведя такие же выкладки, как и в предыдущем случае будем иметь
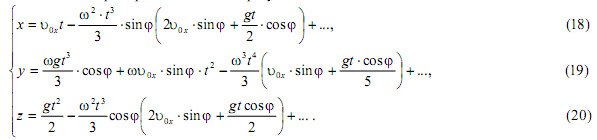
Точка отклоняется на север и на восток (северо - восток). Из формулы (19) видно, что имеются два положительных слагаемых, пропорциональных первой степени угловой скорости ω, причем второе слагаемое появляется из - за начальной скорости, направленной на север. Следовательно, отклонение на восток больше, чем при падении точки в пустоте без начальной скорости. Такой вывод делается с учетом того, что угловая скорости вращения Земли малая по сравнению с единицей величина 
Поэтому членами, содержащими ω в степени выше второй при небольших t и υ0 можно пренебречь.
Вариант III. Пусть 
, т.е. начальная скорость направлена по отвесу вниз. Кориолисова сила инерции за все время падения точки направлена на восток. Решение, полученное аналогично предыдущим двум вариантам, имеет вид
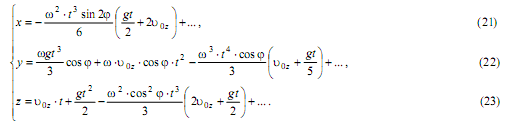
Из (21) видно, что отклонение точки на юг пренебрежимо малó. Формула (22) показывает, что как и в предыдущем варианте, отклонение точки на восток больше, чем при падении без начальной скорости.
Вариант IV. Пусть 
т.е. начальная скорость направлена на запад. Кориолисова сила инерции при t = 0 лежит в плоскости параллели и направлена к оси вращения Земли. Решение дается формулами (15 - 17) с учетом отрицательности знака 
. Если сумма первых двух слагаемых в (16) отрицательна, точка отклоняется в рассматриваемый момент времени на запад и на север (северо - запад), если положительна, то - на север и на восток (северо - восток). Чтобы последний случай имел место, необходимо свободное падение точки в течение сравнительно большого отрезка времени. Например, при 
g = 9,81 м/с точка должна падать более 77 с, т.е. с высоты более 29,1 км. Точка начинает падение в западном направлении, под действием кориолисовой силы инерции поворачивается вправо, пересекает плоскость меридиана и меняет направление на северо -восточное.
Из формулы (17) видно, что пройденное точкой по вертикали расстояние больше в случае, когда начальная скорость направлена на запад. Этому можно дать следующее объяснение. Обратимся к рисункам 2 и 3, где показаны силы, действующие на точку М0 при u0y <0 (рис. 2) и u0y >0 (рис. 3). Для определенности на обоих рисунках величина Fc принята одинаковой. Проекции равнодействующей F¯ двух сходящихся сил и ,ускорения на отвесную линию (ось Z) соответственно равны:
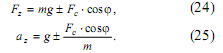
Здесь знак плюс соответствует рисунку 2, знак минус - рисунку 3. Очевидно, что
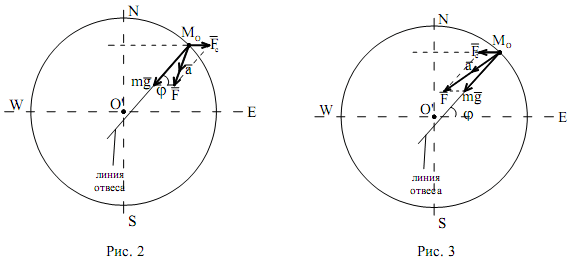
Большее ускорение вызывает в данном случае большую скорость, следовательно, более быстрое падение точки. Такое же объяснение можно дать, опираясь на формулу для модуля равнодействующей
26)
где знаки плюс и минус выбираются так же, как в (24) и (25).
Вариант V. Пусть 
т.е. начальная скорость направлена на юг. Кориолисова сила инерции при t=0 напралена на запад. Решение дается формулами (18) - (20) с учетом знака 
.
Вариант VI. Точка брошена вертикально вверх: 
. Кориолисова сила инерции при подъеме точки почти перпендикулярна плоскости меридиана и направлена на запад. В качестве решения можно использовать формулы (21) - (23), только нужно учитывать, что должны выполняться условия 
.
В этой работе предполагалось, как обычно принято, что точка расположена в Северном полушарии. Можно аналогично решить задачу о движении материальной точки в пустоте вблизи поверхности Земли в Южном полушарии.
Наконец, заметим, что формулы (14) -(23) можно применить для оценки влияния вращения планет Солнечной системы на движение материальной точки вблизи их поверхностей.
СПИСОК ЛИТЕРАТУРЫ
-
Лойцянский Л.Г., Лурье А.И. Курс теоретической механики: В 2-х томах. Т. II. Динамика. - 6-е изд., перераб. и доп. - М.: Наука, Главная редакция физико-математической литературы, 1983. - 640 с.
-
Яблонский А.А., Никифорова В.М. Курс теоретической механики. Учебник для технических вузов. - 8-е изд., стереотипное. - СПб.: Издательство «Лань».- 2001. - 768 с.
-
Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. В двух томах. - СПб.: Издательство «Лань». - 736 с.
- Кильчевский Н.А. Курс теоретической механики, т. I (кинематика, статика, динамика точки). - 2-е изд. - М.: Наука, Главная редакция физико-математической литературы, 1977.
- Задачи и упражнения по математическому анализу. Под редакцией Демидовича Б.П. - М.: Наука, Главная редакция физико-математической литературы, 1978. - 480 с.