Рассмотрим следующий случай из машиностроения. Рабочий изготовил партию деталей в количестве n штук. При этом он стремился, чтобы каждая деталь имела один и тот же размер, указанный на чертеже. Однако такая точность на практике не достижима. Детали имеют разные размеры, хотя и близкие к указанному на чертеже. Самый малый размер детали равен k. Деталей с таким размером - nk штук. Самый большой размер детали равен m. Деталей с таким размером - nm штук. Как известно, частотой события А (или статистической вероятностью события А) в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов [1]. Если под событием А понимать изготовление одной детали, размер которой лежит в пределах от k до x, а nk;x есть количество деталей с размером от k до х, то частота события А для размера х равна ![]() . Тогда
. Тогда ![]() , а
, а ![]() . Совокупность всех значений F(х), когда х принимает значения от k до m, называется интегральным законом распределения величины х (в работе для удобства называется законом распределения).
. Совокупность всех значений F(х), когда х принимает значения от k до m, называется интегральным законом распределения величины х (в работе для удобства называется законом распределения).
Если из указанной партии исключить детали с размером k, то закон распределения размеров оставшихся деталей будет выражаться формулой:
![]()
Функции F(х) и Т(х) связаны линейной зависимостью:
![]()
Чтобы установить общую формулу класса функций F(х), проанализируем выражение:
![]()
В правой его части имеются три члена: F(k) - постоянное слагаемое; ![]() - постоянный множитель; Т(х) - функция. Величина F(k) есть значение функции F(x) в точке k, а величина
- постоянный множитель; Т(х) - функция. Величина F(k) есть значение функции F(x) в точке k, а величина ![]() есть значение функции
есть значение функции ![]() в точке m. Функция Т(х) не зависит от величины nk, т.к. эта функция есть результат исключения данной величины из функции F(х). В таком случае, функция Т(х) не зависит и от величин F(k) и
в точке m. Функция Т(х) не зависит от величины nk, т.к. эта функция есть результат исключения данной величины из функции F(х). В таком случае, функция Т(х) не зависит и от величин F(k) и ![]() , т.к.
, т.к. ![]() . Поэтому величины
. Поэтому величины ![]() и
и ![]() входят в функцию F(х) в качестве независимых параметров, причем: t1 - начальное условие функции F(х); t2 - конечное условие функции
входят в функцию F(х) в качестве независимых параметров, причем: t1 - начальное условие функции F(х); t2 - конечное условие функции ![]() .
.
Общая формула закона распределения должна описывать такое множество функций F(х), в котором для заданных значений k и m имеется бесконечное множество значений t1 и t2, т.к. в противном случае множество функций F(х) будет неполным. Следовательно, в искомом множестве, величины k и m являются определенными, а параметры t1 и t2 - неопределенными. Поскольку функция F(х) содержит эти параметры, то она не может задаваться произвольно. Чтобы перейти от функции F(х) к произвольно задаваемой функции, необходимо исключить из F(х) параметры t1 и t2. Таким образом, мы и установим общую формулу класса функций F(х).
Вычитание из функции F(х) параметра t1 и деление результата на параметр t2 не подходит, поскольку так исключаются только определенные параметры.
Правильный способ исключения указанных параметров заключается в том, что аргументу х придается приращение Δx (т.к. переменная х является независимой, то величина Δx постоянна). Тогда функция F(x) получает приращение:
![]()
Это выражение не содержит параметр t1, но по-прежнему содержит параметр t2.
Приращение ![]() получает приращение:
получает приращение:
![]()
Деление выражения ![]() на выражение
на выражение ![]() приводит к исключению параметра t2. Таким образом, получается выражение:
приводит к исключению параметра t2. Таким образом, получается выражение:
![]()
Оно не содержит параметры t1 и t2. Данное выражение зависит от переменной х и постоянной Δx. Зависимость от Δx указывает на то, что это выражение является не полной функцией, а только частью некоторой полной функции. В данном случае, выражение ![]() является сомножителем полной функции, т.к. оно имеет вид
является сомножителем полной функции, т.к. оно имеет вид ![]() , где f - полная функция. Если П(х) есть произвольно задаваемая функция, то величина
, где f - полная функция. Если П(х) есть произвольно задаваемая функция, то величина ![]() есть ее сомножитель.
есть ее сомножитель.
Существует два пути перехода от сомножителя ![]() к полной функции:
к полной функции:
1. В полной функции не сохраняется функциональная зависимость от х выражения ![]() , х есть величина переменная.
, х есть величина переменная.
2. В полной функции сохраняется функциональная зависимость от х выражения ![]() , х есть величина постоянная.
, х есть величина постоянная.
В первом случае, полная функция есть произведение всех значений величины ![]() , когда х принимает значения от k до х. Это произведение равно
, когда х принимает значения от k до х. Это произведение равно ![]() . Хотя это выражение не содержит параметр t2, но, как сказано выше, так исключаются только определенные параметры. Следовательно, этот случай не подходит.
. Хотя это выражение не содержит параметр t2, но, как сказано выше, так исключаются только определенные параметры. Следовательно, этот случай не подходит.
Во втором случае, полная функция есть произведение, в котором все сомножители одинаковы и равны ![]() . Очевидно, что число этих сомножителей равно количеству отрезков Δx, укладывающихся на отрезке [k;m], т.е. это число равно
. Очевидно, что число этих сомножителей равно количеству отрезков Δx, укладывающихся на отрезке [k;m], т.е. это число равно ![]() . Тогда:
. Тогда:
![]()
Если величина Δx не является бесконечно малой, то она содержится в этой функции, что не допустимо. Следовательно, величина Δx является бесконечно малой, т.е. Δx =dx. Тогда:
![]()
Отсюда общая формула закона распределения в дифференциальной форме выглядит так:
![]() ,
,
где: П(х) - произвольно задаваемая функция.
При задании функции П(х), в нее вводится некоторый объем информации. В результате интегрирования указанного уравнения, эта информация попадает в функцию F(x) в искаженном виде. Следовательно, при обратном процессе, когда переходят от функции F(x) к функции П(х), будет происходить корректировка информации.
Совершенно очевидно, что нормальное распределение будет иметь место, когда условия эксперимента являются идеальными. В этом случае, функция П(х) содержит минимальный объем информации и представляет собой линейную зависимость от х, т.е. ![]() , где с и d - постоянные. Однако, при таком условии, функция F(x) не может быть выражена в элементарных функциях.
, где с и d - постоянные. Однако, при таком условии, функция F(x) не может быть выражена в элементарных функциях.
Если П(х) равно 1-x и все значения х находятся вблизи 0, то справедливо следующее приближенное равенство:
![]()
Тогда:
![]()
Проинтегрируем это выражение, полагая х в пределах от m до х:
![]()
Откуда:
![]() ,
,
т.е. мы пришли к закону Гаусса.
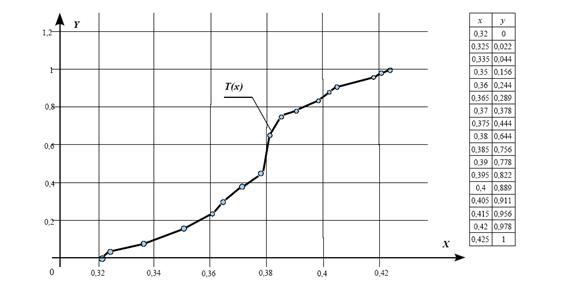
Рис. 1. Закон распределения размеров деталей (случай из практики)
Функции F(х) и Т(х) являются монотонно возрастающими, при этом на практике кривые этих функций имеют множество точек перегиба (Рис.1). Вследствие этого, значения функций ![]() и
и ![]() колеблются вокруг некоторых средних значений этих функций. В этом случае общая формула закона распределения в дифференциальной форме является неприменимой. Она становится применимой после замены функций
колеблются вокруг некоторых средних значений этих функций. В этом случае общая формула закона распределения в дифференциальной форме является неприменимой. Она становится применимой после замены функций ![]() и
и ![]() их средними значениями.
их средними значениями.
Пусть Б(х) есть функция, представляющая собой средние значения функции ![]() в интервале [k;x]. Так как функция
в интервале [k;x]. Так как функция ![]() является слагаемым функции F(х), то эти значения находятся как средние арифметические, т.е. из функции F(x) вычитается ее значение в точке k, а результат делится на (x-k):
является слагаемым функции F(х), то эти значения находятся как средние арифметические, т.е. из функции F(x) вычитается ее значение в точке k, а результат делится на (x-k):
![]()
В точке k значение функции Б(х) является неопределенным: ![]() . В точке m эта функция имеет определенное значение:
. В точке m эта функция имеет определенное значение:
![]()
Следовательно, средние значения функции ![]() необходимо искать в интервале [x;m]. Так как функция
необходимо искать в интервале [x;m]. Так как функция ![]() является сомножителем функции Б(х), то эти значения находятся как средние геометрические, т.е. функция Б(х) делится на ее значение в точке m, а из результата извлекается корень степени (m-x). Полученная функция будет равна
является сомножителем функции Б(х), то эти значения находятся как средние геометрические, т.е. функция Б(х) делится на ее значение в точке m, а из результата извлекается корень степени (m-x). Полученная функция будет равна ![]() :
:
![]()
Откуда:
![]()
Окончательно:
![]() ,
,
где: П(х) - произвольно задаваемая функция. Это - общая формула закона распределения для средних значений. Тогда:
![]()
Эта формула незаменима в практических исследованиях, поэтому остановимся на ней подробнее.
Формула для плотности распределения ![]() имеет следующий вид:
имеет следующий вид:
![]()
В точках k и m эта функция принимает следующие значения:
![]() ;
; ![]()
Для проведения исследований, необходимо установить точные значения функции Т(х) во всех точках, для которых имеются экспериментальные данные. Некоторые исследователи, стремясь сделать график функции Т(х) более плавным, несколько изменяют значения функции Т(х), что делать не рекомендуется, т.к. результатом может быть существенная ошибка в исследовании. Далее, на основании имеющихся значений функции Т(х) устанавливаются значения функции П(х). Это выполняется при помощи следующей формулы:
![]()
Как было сказано выше, если условия эксперимента являются идеальными, то функция П(х) содержит минимальный объем информации и представляет собой линейную зависимость от х. Простейшим случаем такого распределения является прямая ![]() когда
когда ![]() . При превышении минимального объема, зависимость П(х) от х становится нелинейной. Если такое превышение незначительно, то кривая П(х) не имеет экстремумов. Если превышение значительно, то на кривой П(х) появятся экстремумы (Рис. 2). Они могут сигнализировать о том, что:
. При превышении минимального объема, зависимость П(х) от х становится нелинейной. Если такое превышение незначительно, то кривая П(х) не имеет экстремумов. Если превышение значительно, то на кривой П(х) появятся экстремумы (Рис. 2). Они могут сигнализировать о том, что:
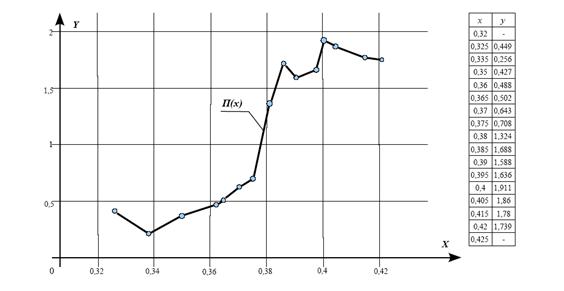
Рис. 2. Функция П(х), соответствующая функции Т(х) на Рис. 1.
1. Материал заготовок имеет дефект в интервале распределения.
2. Механизм подачи станка имеет дефект в том положении, когда режущая кромка резца находится в интервале распределения .
3. Инструмент, который использовался для измерения готовых деталей, имеет дефект в интервале распределения.
4. Метод измерения готовых деталей давал наибольшую ошибку в интервале распределения и т.д.
Практический пример из машиностроения. Токарь изготовил большую партию деталей «Пробка». На чертеже указан диаметр пробки: ![]() (мм). Из этой партии наугад выбраны 46 деталей. При замере оказалось, что их диаметры лежат в пределах от 29,575 мм до 29,68 мм. Так как в данном случае размер готовой детали меньше размера заготовки, то величина х будет представлять собой разность между размером 30 мм и размером готовой детали. Тогда х лежит в пределах от 0,32 мм до 0,425 мм. Кривая распределения величины х Т(х) показана на Рис 1. Соответствующая ей кривая П(х) показана на Рис.2. На ней имеются 4 экстремума. Два экстремума в начале и конце объясняются тем, что интервал распределения у выбранных деталей не совпадает с действительным интервалом распределения. Два других экстремума объясняются некоторой неточностью метода измерения.
(мм). Из этой партии наугад выбраны 46 деталей. При замере оказалось, что их диаметры лежат в пределах от 29,575 мм до 29,68 мм. Так как в данном случае размер готовой детали меньше размера заготовки, то величина х будет представлять собой разность между размером 30 мм и размером готовой детали. Тогда х лежит в пределах от 0,32 мм до 0,425 мм. Кривая распределения величины х Т(х) показана на Рис 1. Соответствующая ей кривая П(х) показана на Рис.2. На ней имеются 4 экстремума. Два экстремума в начале и конце объясняются тем, что интервал распределения у выбранных деталей не совпадает с действительным интервалом распределения. Два других экстремума объясняются некоторой неточностью метода измерения.
СПИСОК ЛИТЕРАТУРЫ:
- Вентцель Е.С. Теория вероятностей. - М.: Наука, 1969 - 28-29 с.
Библиографическая ссылка
Окунев И.В. ЗАКОН РАСПРЕДЕЛЕНИЯ // Фундаментальные исследования. – 2009. – № 2. – С. 8-14;URL: https://fundamental-research.ru/ru/article/view?id=1787 (дата обращения: 25.04.2024).



