Пролапс митрального клапана (ПМК) относится к проявлениям дисплазии соединительной ткани сердца (ДСТС). ДСТС - это группа наследуемых или врожденных нарушений соединительной ткани полигенно-мультифакториальной природы, наиболее распространенным проявлением которого является ПМК. Данная патология привлекает к себе пристальное внимание исследователей по ряду причин. Это связано с большой частотой ПМК в популяции, кроме того велик риск развития таких осложнений, как нарушения ритма и проводимости сердца, тромбоэмболия различных сосудов и внезапная смерть [1, 2]. Своевременная диагностика и оценка клинического значения ПМК является актуальной проблемой для больных кардиологического профиля, особенно среди детей и подростков. В последние годы ПМК интенсивно изучается, благодаря возросшим техническим возможностям и внедрению в клиническую практику методов эхокардиографии. По мнению большинства авторов, основу патогенеза идиопатического ПМК составляют генетически детерминированные нарушения различных компонентов соединительной ткани, что приводит к «слабости» створок митрального клапана и их провисанию в полость левого предсердия. У пациентов с идиопатическим ПМК обнаружены особенности строения соединительной ткани створок митрального клапана: увеличение содержания гиалуроновой кислоты, сульфатированных протеогликанов, коллагена I и III типов.
Важное практическое и теоретическое значение имеет исследование внутрисердечной гемодинамики при различной степени данной патологии. В литературе известны математические модели нормальной гемодинамики митрального клапана, однако, в представленных моделях рассматривается только часть сердечного цикла без учета патологии клапана [3, 4, 5, 6].
Цель исследования - математическое моделирование динамики объема и давления левых камер сердца в норме и при ПМК с митральной регургитацией на основе фазовой структуры сердечного цикла.
Материалы и методы исследования
В исследовании проводилось сопоставление клинико-инструментальных данных, эхокардиографических параметров с результатами математического моделирования. Обследовано 76 детей с ПМК, 45 девочек и 31 мальчик, в возрасте от 9 до 18 лет (средний возраст -12,9 ± 4,1). В зависимости от степени ДСТС дети были разделены на 2 группы: I - 37 детей с ПМК 1-й степени и умеренной митральной регургитацией (MR), фракция регургитирующего объема (RF) < 30 %), II - 39 пациентов с ПМК 2-й степени и выраженной MR (30 % < RF < 47 %). Эхокардиография (ЭхоКГ) выполнялась по общепринятой методике в двухмерном режиме на аппарате «Vivid 7» (GE). Критерием ПМК являлось систолическое смещение одной или обеих створок митрального клапана в полость левого предсердия на 2 мм и более из трансторакального доступа парастернальной позиции по длинной оси [1]. При ЭхоКГ определяли диаметр и объем левого и правого предсердий, конечно-систолический и диастолический размеры полости левого и правого желудочков. Также оценивался тип гемодинамики, ударный объём, фракция выброса, толщина миокарда ЛЖ. По данным цветового допплеровского картирования, определялась степень MR. Расчет фракции регургитирующего объема (RF) проводился с использованием уравнения непрерывности потока. Статистическая обработка полученных результатов проводилась с использованием прикладного пакета статистических программ, рекомендованного ВАК РФ Statistica 7.0 (StatSoft, USA). Различия считались статистически достоверными при р < 0,05.
Результаты исследования и их обсуждение
Система клапанов сердца: аортального, митрального, трикуспидального, легочного обеспечивает однонаправленное движение тока крови в системе кровообращения. Фазовая структура сердечного цикла разделяется на систолу и диастолу. Каждый из этих периодов, в свою очередь, подразделяется на ряд фаз и интервалов, характеризующих различные этапы динамики сердца [7, 8].
Рассмотрим построение модели заполнения желудочков сердца в фазу диастолы и их опорожнение в систолу. На протяжении общей систолы желудочков наблюдается два различных по своей физиологической сущности периода: период напряжения и период изгнания. Во время периода напряжения совершается подготовка сердца к изгнанию крови в магистральные сосуды. Данный период общей систолы физиологически неоднороден. В начале периода напряжения совершается деполяризация волокон сердечной мышцы и начинается охват миокарда желудочков сократительным процессом. Внутрижелудочковое давление при этом не повышается, так как в миокарде наряду с напряженными участками имеются участки, находящиеся в состоянии расслабления. Данный период обозначается как фаза асинхронного сокращения [9, 10].
При последующем напряжении волокон миокарда давление в полостях сердца начинает повышаться, закрываются атриовентрикулярные клапаны, и наступает вторая часть периода напряжения - фаза изоволюметрического сокращения. Во время этой фазы внутрижелудочковое давление повышается до величины давления в аорте (или легочной артерии). Как только давление в желудочке и магистральных сосудах становится одинаковым, открываются полулуния аортального клапана и клапана легочной артерии, начинается второй период систолы - период изгнания.
Таким образом, расход крови в систолу можно представить в виде уравнения:
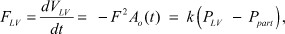 (1)
(1)
где
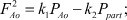 (2)
(2)
следовательно
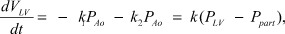 (3)
(3)
где FLV - кровоток из левого желудочка, FAo - кровоток через выходной тракт в аорту, давление в полости левого желудка, Рpart - давление в области периферических артерий, k - коэффициент расхода крови в систолу, k1 - коэффициент перепада давления в восходящем отделе аорты в систолу, k2 - коэффициент перепада давления в периферических артериях в систолу.
Подставив в уравнение средние величины параметров [10], расход крови можно представить как отношение ударного объема (УО) к частоте сердечных сокращений (УО - 60 ml, время систолического изгнания - 0,4 с). Так как систолическое давление в левом желудочке составляет 120 мм рт. ст., а артериальное давление в области периферических артерий 70 мм рт. ст., следовательно, коэффициент расхода крови в системе кровообращения будет равен:
60 ml/0,4 с = k(120 - 70) мм Hg;
150 ml/с = k 50 мм Hg; k = 3.
Общая систола характеризует собой время, в течение которого в миокарде желудочков наблюдается сократительный процесс. Рассмотрим динамику изменения объема полости левого желудочка в систолу и диастолу и их соотношение с кривой изменения артериального давления в левом желудочке.
В период t = 0 объем полости левого желудочка - VLV будет равен VLV0
VLV = VLV0. (4)
При этом конечно-диастолический объем полости левого желудочка можно представить в виде уравнения:
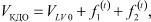 (5)
(5)
где VКДО - конечно-диастолический объем, VLV0 - начальный диастолический объем,
f1(t) - функция роста диастолического объема в период пассивного наполнения, f2(t) - функция роста давления в период систолы левого предсердия.
Уравнение динамики изменения конечно-систолического объема полости левого желудочка будет иметь вид:
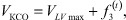 (6)
(6)
где VКСО - конечно-систолический объем, VLVmax - максимальный объем левого желудочка, f3(t) - функция изменения объема левого желудочка в систолу.
При ПМК происходит провисание одной или обеих створок клапана в систолу, что нередко приводит к обратному току крови в полость левого предсердия и развитию недостаточности кровообращения. Сопутствующая миксоматозная дегенерация створок митрального клапана, по данным Гнусаева С.Ф. [11], в 100 % случаев сопровождается митральной недостаточностью.
Изменение кровотока при ПМК определяется разностью давлений в полости левого желудочка и левого предсердия. Помимо этого, прирост кровотока в левом предсердии в период изоволюметрического сокращения будет определяться остаточным объемом, давлением в легочных венах и разницей давлений в левом желудочке и левом предсердии.
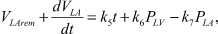 (7)
(7)
где VLArem - остаточный объем; PLV - давление в левом желудочке; PLA - давление в левом предсердии; k5 - коэффициент изменения давления в легочных венах; k6 - коэффициент изменения давления в левом желудочке; k7 - коэффициент разности давлений между левым желудочком и левым предсердием.
Давление в полости левого желудочка при ПМК будет увеличиваться за счет увеличения времени изгнания крови из полости левого предсердия с дополнительным объемом митральной регургитации, которое можно представить в виде:
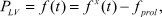 (8)
(8)
где PLV - давление в полости левого желудочка; f(t) - функция роста давления в левом желудочке в зависимости от времени; fx(t) - функция изменения давления в левом желудочке в систолу; fprol - функция изменения давления за счет митральной регургитации при ПМК.
ПМК, наряду с ростом внутрисердечного давления, характеризуется особенностями динамики кривой давления в период сердечного цикла.
Изменение объема полости левого желудочка при ПМК можно представить в виде уравнения:
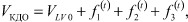 (9)
(9)
где VКДО - конечно-диастолический объем, VLV0 - начальный диастолический объем, f1(t) - функция роста диастолического объема в период быстрого пассивного наполнения, f2(t) - функция роста давления в период систолы левого предсердия, f(t) - функция изменения объема при ПМК.
Минутный объем сердца можно рассчитать как отношение разности давления в аорте и периферических артериях к общему периферическому сопротивлению.
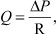
где Q - минутный объем; ΔР - разность давления в аорте и периферических артериях; R - общее периферическое сопротивление.
Объем левого желудочка в систолу будет равен разности максимального объема и минутного объема:
VLV = VКДО - Qt, (10)
где VКДО - конечно-диастолический объем левого желудочка; Q - минутный объем; t - время сердечного цикла.
t = Ts⋅VLv = VLV0, (11)
где Ts - время систолы левого желудочка; VLv - объем левого желудочка; VLV0 - остаточный объем или конечно-систолический объем левого желудочка.
Изменение объема полости левого желудочка при избыточном переполнении полости желудочка при ПМК с митральной регургитацией будет также зависеть от жесткости и упругости миокарда. Жесткость миокарда левого желудочка можно представить в виде отношения:
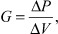 (12)
(12)
где ΔР - градиент давления в полости левого желудочка; ΔV - прирост объема в полости левого желудочка.
Прирост объема полости левого желудочка при ПМК с митральной регургитацией также взаимосвязан с упругостью миокарда левого желудочка. Упругость миокарда можно рассчитать как отношение:
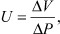 (13)
(13)
где ΔР - градиент давления в полости левого желудочка, ΔV - прирост объема в полости левого желудочка.
В таблице представлены параметры внутрисердечной гемодинамики по группам у детей с различной степенью ПМК, рассчитанные методами эхокардиографии и математического моделирования. Полученные основные данные гемодинамики оказались сопоставимы, при этом достоверные различия (p < 0,05) обнаружены только во II группе детей с ПМК 2-й степени и выраженной MR и касались показателей КДО, КСО.
Сопоставление эхокардиографических данных и результатов математического моделирования у детей с ПМК
|
Параметры гемодинамики |
ЭхоКГ I группа (n = 37) |
Матем. мод. (n = 37) |
ЭхоКГ |
Матем. мод. |
|
1. Пиковое систолическое давление в ЛЖ, мм рт. ст. |
102,4 ± 0,3 |
98,1 ± 1,5 |
119,6 ± 0,4 |
116,3 ± 0,8 |
|
2. Среднее давление в ЛП, мм рт. ст. |
7,1 ± 1,1 |
6,6 ± 0,4 |
8,2 ± 0,7 |
9,3 ± 0,9 |
|
3. Конечно-диастолический объем ЛЖ, мл |
78,9 ± 1,9 |
82,9 ± 1,7 |
102,3 ± 2,8 |
119,2 ± 2,3* |
|
4. Конечно-систолический объем ЛЖ, мл |
24,3 ± 1,2 |
21,4 ± 1,0 |
36,1 ± 1,2 |
45,7 ± 1,4* |
|
5. Максимальный объем ЛП, мл |
41,0 ± 1,5 |
46,4 ± 1,1 |
53,4 ± 1,4 |
61,7 ± 1,5 |
|
6. Ударный объем, мл |
54,6 ± 1,3 |
99,5 ± 1,2 |
66,2 ± 1,3 |
54,5 ± 1,6 |
|
7. Фракция выброса, % |
69,2 ± 1,4 |
72,3 ± 1,7 |
64,7 ± 1,1 |
61,1 ± 1,8 |
|
8. Минутный объем, л/мин |
5,2 ± 0,7 |
5,9 ± 0,3 |
6,8 ± 0,4 |
7,4 ± 0,2 |
Примечание: * - различия достоверны (p < 0,05) при сравнении параметров гемодинамики рассчитанных методов ЭхоКГ и математического моделирования.
Полученные данные позволили создать предпосылки для формирования базы данных по нарушениям внутрисердечной гемодинамики при различной патологии митрального клапана. Соотношение параметров объем-давление в левом желудочке и левом предсердии в зависимости от времени систоло-диастолического периода явилось клинически значимым в оценке степени расстройств внутрисердечной гемодинамики. На основе полученных результатов определены подходы к кодированию и декодированию данных банка в целях многократного их использования.
Предложенный математический аппарат позволяет получить консолидированную информацию о состоянии пациента, а также осуществить ее кодирование. Использование результатов данной работы возможно не только в области диагностики и оценки эффективности лечения пациентов с ПМК, но и при составлении прогноза заболевания.
Выводы
1. Разработана математическая модель гемодинамики левых камер сердца на основе фазовой структуры сердечного цикла, позволяющая оценить параметры глобальной функции левого желудочка.
2. На основе модельного анализа определены характерные изменения давления и объема левых отделов в норме и при ПМК.
3. Определены закономерности изменения объема и давления полости левого желудочка, инотропной функции и степени митральной регургитации при ПМК.
4. Создана база данных по нарушениям внутрисердечной гемодинамики при различной степени ПМК, определены подходы к кодированию и декодированию данных банка для многократного их использования.
Список литературы
- Земцовский Э.В. Пролапс митрального клапана. - СПб.: Изд-во «Общество Знание», 2010. - 160 с.
- Otto C.M., Pearlman A.S. Textbook of Clinical echocardiography. - Philadelphia, Lond., Toronto. - 2007. - P. 1239-1247.
- Einstein D.R., Kunzelman K.S., Reinhall P.G., Nicosia M.A., Cochran R.P. Nonlinear fluid-coupled computational model of the mitral valve // J. Heart Valve Dis. - 2005. - №14. - С. 376-385.
- Kunzelman K.S., Einstein D.R., Cochran R.P. Fluid-structure interaction models of the mitral valve: function in normal and pathological states. - Phil. Trans. R. Soc. B (2007) 362. - С. 1393-1406.
- Szabó G., Soans D., Graf A., Bellera C.J., Waite L., Hagl S. A new computer model of mitral valve hemodynamics during ventricular filling // Eur. J. Cardio-thoracic Surgery. - 2004. - №26. - С. 239-247.
- McQueen D.M., Peskin C.S., Yellin E.L. Fluid dynamics of the mitral valve: physiological aspects of a mathematical model // Am. J. Physiol. - 1982. - №242. - H1095-H1110.
- Волькенштейн М.В. Физика мышечного сокращения // Успехи физических наук. - 1970. - Т. 100, № 4. - С. 681-703.
- Brutsaert D.L., Claes V.A., Sonnenblick E.H. Velocity of shortening of unloaded heart muscle and the length-tension relation. Circ. Res. (1971) 29, с. 63-75.
- Williams Jr. F.J., Potter R.D., Hern D.L., Mathew B., Deiss Jr. W.P. Hydroxyproline and passive stiffness of pressure-induced hypertrophied kitten myocardium // J. Clin. Invest. - 1982. - №69. - Р. 309-314.
- Кассирский И.А. Справочник по функциональной диагностике. - М.: Медицина, 1970. - 848 с.
- Гнусаев С.Ф., Белозеров Ю.М., Виноградов А.Ф. Клиническое значение малых аномалий сердца у детей // Российский вестник перинатологии и педиатрии. - 2006. - №4. - С. 32-33.
Рецензент -
Шейх-Заде Ю.Р., д.м.н., профессор кафедры нормальной физиологии ГОУ ВПО «Кубанский государственный медицинский университет Федерального агентства здравоохранения и социального развития», г. Краснодар.
Работа поступила в редакцию 08.02.2011.
Библиографическая ссылка
Домницкий М.В., Чернова Т.А., Клюев А.А. МОДЕЛИРОВАНИЕ ВНУТРИСЕРДЕЧНОЙ ГЕМОДИНАМИКИ ПРИ ПРОЛАПСЕ МИТРАЛЬНОГО КЛАПАНА НА ОСНОВЕ ФАЗОВОЙ СТРУКТУРЫ СЕРДЕЧНОГО ЦИКЛА // Фундаментальные исследования. – 2011. – № 8-1. – С. 120-123;URL: https://fundamental-research.ru/ru/article/view?id=26797 (дата обращения: 25.04.2024).



