Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова

Балданова Д.М., Танганов Б.Б., Балданов М.М.

На основе теоремы Ирншоу и критерия устойчивости по Ляпунову показано, что распределение вещества и зарядов в растворах электролитов не является статическим по Дебаю–Хюккелю, а характеризуется малыми гармоническими колебаниями.

Статья в формате PDF

620 KB

электролиты

теория Дебая-Хюккеля

устойчивость

теорема Ирншоу

колебания

В основе современной теории растворов электролитов и различных ее модификаций лежат представления классической теории Дебая и Хюккеля об ионной атмосфере и электрохимических подвижностях ионов. Данная теория является теорией предельного разбавления. В более концентрированных растворах наступает заметное отклонение свойств от тех, которые предсказываются данной теорией.

На наш взгляд, это связано с тем, что, во-первых, основное уравнение Дебая-Хюккеля в виде [5]

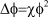 (1)

было получено в предположении, что 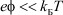 в функции распределения Больцмана для плотности заряда:

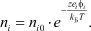 (2)

Данное условие, в свою очередь, предполагает малые концентрации электролита, т.е. когда расстояния между ионами значительные. Только в этом случае возможна кулоновская аппроксимация потенциала Φ при разложении экспоненты 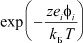 в ряд Маклорена:

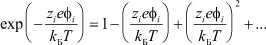
Следовательно, теория Дебая-Хюккеля, по определению, является теорией разбавленных растворов, во-первых, все попытки ее модификации для более концентрированных растворов (С > 10^-2 м) в рамках этой теории, не имеют реальной основы, поскольку требуют введения подгоночных параметров.

Во-вторых, необходимо отметить противоречие электростатической теории растворов Дебая-Хюккеля с фундаментальной теоремой Ирншоу [9]. Согласно данной теореме, «...любое статическое распределение зарядов не имеет устойчивых состояний... Устойчивость электростатической модели можно обеспечить введением неэлектростатических сил». Следовательно, распределение вещества и зарядов в растворах электролитов, по Дебаю-Хюккелю, является неподвижным и статическим, т.е. растворы электролитов тем самым не имеют устойчивых состояний.

В действительности, молекулы растворителя в сольватном комплексе совершают регулярные колебания от своих равновесных координат, что порождает локальные изменения плотности зарядов.

Наглядную картину таких колебаний можно установить в виде смещения равновесия диссоциации некоторого электролита в произвольном растворителе

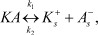 (3)

где 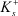,  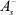- сольватированные ионы; k₁, k₂ - кинетические константы скоростей прямой и обратной реакций. Если k₁ >> k₂, то электролит KA является сильным, а при k₁ << k₂ -
слабым. Столкновение ионов 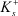 и 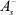 приводит к образованию ионных ассоциатов или обратной рекомбинации с образованием молекул. При смещении равновесия системы (3) вправо (u₁ > u₂) плотность зарядов  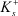 и 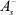  увеличивается. При смещении же равновесия влево (u₁ < u₂) плотность зарядов уменьшается. При фиксированной концентрации вещества средняя длина свободного пробега ионов  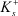и 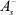 конечна. Согласно общим положениям механики, любое одномерное конечное движение есть колебательное [6].

Для раскрытия физического содержания этих колебаний необходимо провести кинетический анализ диссоциации процесса равновесия (3).

Данный процесс (3) характеризует система уравнений [8]:

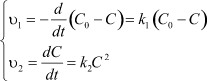 (4a) (4б)

где C₀ - начальная концентрация электролита; C - концентрация диссоциированных молекул электролита; C₀ - C = d - концентрация недиссоциированных молекул.

Приведенная система уравнений соответствует общим положениям понятия химического равновесия. Так, при u₁ = u₂ получаем константу равновесия

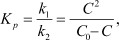
соответствующую закону разбавления Оствальда.

Структура уравнения диссоциации (3) предполагает использование критерия устойчивости по Ляпунову. Привлекательность использования данной устойчивости состоит в том, что она позволяет привлечь методы формальной кинетики в виде уравнений (4а) и (4б) при кинетическом анализе равновесия диссоциации некоторого электролита. Согласно данному критерию, некоторая произвольная функция V(y) непрерывно дифференцируема при следующих условиях: V(y) > 0 при y ≠ 0, V(0) = 0 при y = 0

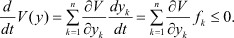 (5)

Для исследуемой системы уравнений (4), параметру y соответствует концентрация C:

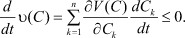 (6)

Если 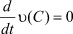, то устойчивость слабая. Если же 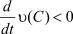, то устойчивость сильная, даже асимптотическая.

Нам представляется интересным вариант условия (6), когда возможны асимптотические устойчивости и вероятны предельные циклы на фазовой плоскости.

Так, для прямой реакции, обеспечивающей генерацию ионов условие (6) приобретает вид:

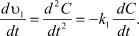 (7)

Поскольку скорости u₁ и u₂ в (4а) и (4б) являются сопряженными величинами, то в уравнении (7) вместо 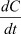 можно взять его значение для u₂ из выражения (4б). Тогда:

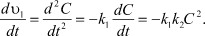 (8)

Так как C = C₀ - δ, возможно представить выражение (7) в виде:

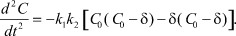 (9)

Для сильных электролитов, можно пренебречь вторым слагаемым в правой части. Тогда при C = C₀ - δ имеет место:

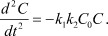 (10)

А это есть уравнение гармонических колебаний с решением

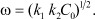 (11)

По существу уравнение (11) является частотой популяционных колебаний Лотка-Вольтерра [4].

Следующим моментом, который необходимо отметить, является то, что в уравнении (1) величина

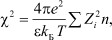 (12)

есть не что иное, как дебаевский радиус экранирования, рассматриваемый в современной теории плазмы (газовой плазме, твердотельной плазме и плазме в растворах электролитов) в виде [1]:

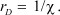 (13)

По определению, дебаевский радиус представляет собой расстояние, на которое проникает в плазму внешнее электростатическое поле, нейтрализуемое полями диполей молекул растворителя, индуцированными вследствие поляризации среды:

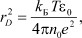 (14)

где ε₀ - диэлектрическая постоянная среды [8]. В растворах электролитов данную величину рассматривают в виде

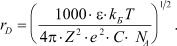
Можно дать и другое определение дебаевскому радиусу, согласно которому, дебаевский радиус r_D представляет собой расстояние, на которое заряды в плазме собираются вокруг рассматриваемого заряда и экранируют его поле [3]. Данное определение является более точным для физики плазмы, поскольку дебаевский радиус, по порядку величины, равен расстоянию, которое заряд с тепловой скоростью 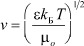 проходит за один период колебаний , отвечающий частоте плазменных колебаний [10]:

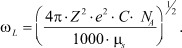 (15)

Плазменная частота характеризует малое изменение плотности заряда относительно его среднего значения в режиме малых гармонических колебаний [3, 7], что и было показано уравнением (11).

Очевидно, что эти плазменные колебания обеспечивают устойчивость систем зарядов в соответствии с теоремой Ирншоу и формализуют энергию коллективных многочастичных взаимодействий ионов в форме:

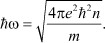
Таким образом, электростатическая теория Дебая-Хюккеля, правильно формализующая один из основных параметров плазменного состояния вещества - дебаевский радиус r_D, не учитывает, что это понятие является сопряженным с плазменной частотой, т.е. наличию в растворах электролитов продольных акустических колебаний совокупности ионов с частотой ω₀.

Вместе с тем, отдельные фрагменты данной теории свидетельствуют о перспективности привлечения для описания состояния ионов в растворах электролитов гидродинамического приближения на основе моделей ассоциативных равновесий и закономерностей движения частиц в вязкой среде, широко используемого в физике газовой и твердотельной плазмы [2].

Список литературы

1. Александров А.Ф., Богданкевич Л.С., Рухадзе А.А. Основы электродинамики. - М.: Высшая школа, 1988. - С. 6.
2. Плазменно-гидродинамическая теория растворов электролитов и электропроводность / М.М. Балданов, Д.М. Балданова, С.Б. Жигжитова, Б.Б. Танганов // Доклады АН ВШ РФ. - 2006. - №1(6). - С. 25-33.
3. Гинзбург В.Л. Распространение электромагнитных волн в плазме. - М.: Наука, 1967. - 683 с.
4. Гленсдорф П. Термодинамическая теория структуры, устойчивости и флуктуации / П. Гленсдорф, И. Пригожин. - М.: Мир, 1973. - 324 с.
5. Дебай П. Избранные труды. - Л.: Наука, 1987. - 559 с.
6. Ландау Л.Д. Механика / Л.Д. Ландау, Е.М. Лифшиц. - М.: Наука, 1973. - 208 с.
7. Платцман Ф. Волны и взаимодействия в плазме твердого тела / Ф. Платцман, П. Вольф. - М.: Мир, 1975. - 436 с.
8. Робинсон Р. Растворы электролитов / Р. Робинсон, Р. Стокс. - М.: ИЛ, 1963. - 646 с.
9. Тамм И.Е. Основы теории электричества. - М.: Наука, 1989. - 504 с.
10. Langmur J., Tonks A. // J. Phys.Rev. - 1927. - Vol. 33. - P. 195.

Рецензенты:

Анцупова Т.П., д.б.н., профессор кафедры неорганической и аналитической химии, Восточно-Сибирский государственный технологический университет, г. Улан-Уде;

Базарова Ж.Г., д.х.н., профессор, зав. лабораторией оксидных систем, Байкальский институт природопользования СО РАН, г. Улан-Уде;

Виноградова М.Г., д.х.н., профессор, профессор кафедры физической химии ГОУ ВПО «Тверской государственный университет», г. Тверь;

Полещук О.Х., д.х.н., профессор, зав. кафедрой органической химии, Томский государственный педагогический университет, Министерства науки и образования РФ, г. Томск.

Работа поступила в редакцию 28.01.2011.

Библиографическая ссылка