В начале 1970-х годов была предложена концепция использования в электрических цепях нового пассивного элемента - мемристора [2]. Исследователи из лаборатории HP Labs в 2008 году создали работающий прототип мемристора [5], главной отличительной особенностью которого является то, что он может сохранять свое состояние (сопротивление) при отсутствии питания. Применение мемристоров в вычислительных системах делает возможным улучшение показателей их энергоэффективности, а также позволяет создавать надежные и высокоинтегрированные аналоговые компьютеры, многоуровневую логику и нейронные
системы.
Мемристор представляет собой структуру металл-диэлектрик-металл, в которой в качестве диэлектрика обычно используется тонкая пленка диоксида титана (TiO2) [5]. Изменение сопротивления при прохождении тока через мемристор в большей мере связано с модуляцией ионной проводимости, которая обусловлена перемещением вакансий кислорода в диэлектрике [4].
С уменьшением топологических размеров мемристоров эффект мемризистивности и нелинейность величин дрейфа носителей заряда проявляется сильнее, поэтому для моделирования и проектирования микросхем на основе мемристоров необходимо как можно точнее учитывать параметры изменения мемризистивности в схемных моделях компонентов.
На рис. 1 представлена схемотехническая модель мемристора [1].
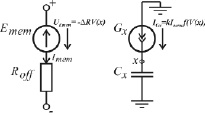
Рис. 1. Эквивалентная схема
мемристора из [1]
Ток Imem, проходящий через Roff (эквивалентное сопротивление мемристора при толщине обедненной кислородом области w, равной 0), оказывает влияние на генератор тока Gx, который будет создавать ток, численно равный:
kImemf(V(x)), (1)
где х - отношение толщины обедненной области (насыщенной вакансиями кислорода) w к общей толщине слоя диоксида титана L (x ∈ (0,1)); V(x) – функция, возвращающая численное значение x в вольтах.
Коэффициент k из формулы (1) определяется с помощью заданных технологических параметров:
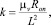 (2)
(2)
где mv – подвижность носителей заряда;
Ron – эквивалентное сопротивление мемристора при толщине обедненной кислородом области w равной L (т.е. в открытом состоянии).
Функция f(х) в (1) выполняет корректировку нелинейности дрейфа примеси и рассчитывается по формуле [3]:
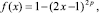 (3)
(3)
где p – положительный корректирующий коэффициент, p ∈ [1, ∞).
Корректирующая функция f(x) принимает значения от 0 до 1 (рис. 2), причем в крайних точках она равна 0.
На рис. 1 конденсатор Cx выполняет роль интегратора тока генератора Gx.
Параметр x также оказывает влияние на источник напряжения, численное значение напряжения которого (Emem) рассчитывается по формуле:
–DRV(x), (4)
где DR = Roff – Ron.
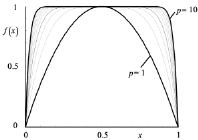
Рис. 2. Семейство графиков функции f(x)
К недостатку описанной модели можно отнести невозможность многократно изменять сопротивление мемристора, т.е. при граничных значениях функции f(x) = 0, мемристор уже не может изменить свое состояние (модель подходит для описания элементов с однократной записью) [1].
Для моделирования мемристоров, применяемых в качестве элементов оперативной памяти, необходима приближенная к реальности функциональная модель, которую можно будет использовать в средствах проектирования СБИС, таких как САПР Cadence.
Авторами предлагается схемотехническая модель, учитывающая особенности функционирования мемристора в качестве элемента памяти. Структурная схема представлена на рис. 3.

Рис. 3. Структурная схема модели мемристора
Основными блоками схемы являются (номера соответствуют обозначениям на рисунке):
1) сенсор тока мемристора (А);
2) блок управления сопротивлением мемристора (БУСМ);
3) умножитель;
4) блок управления порогами ограничения (БУПО);
5) интегратор;
6) функциональный блок (функция f(х));
7) константа, отражающая физико-топологические свойства мемристора (k).
Для реализации и использования предложенной схемотехнической модели мемристора в САПР Cadence были разработаны следующие функциональные блоки:
• источник напряжения, контролируемый напряжением (vcvs);
• умножитель (mult);
• сумматор (sum);
• усилитель с ограничением (amp);
• функциональный блок (func);
• источник тока, контролируемый напряжением (vccs).
Модель мемристора в виде схемы из функциональных блоков, описанных на языке Spectre (САПР Cadence), и стандартных компонентов схемного редактора Cadence Schematic Composer показана на рис. 4.
На представленной схеме (см. рис. 4) резистор R2, сопротивление которого принято равным 1 Ом, и сумматор (блок sum1) преобразуют численное значение тока мемристора в то же значение напряжения. Далее блок mult1 умножает ток мемристора (теперь в виде уровня напряжения) на коэффициент k (физико-топологический параметр), численно равный напряжению источника vdc1. Затем, блок mult2 умножает полученный результат на значение функции f(x) (блок func).
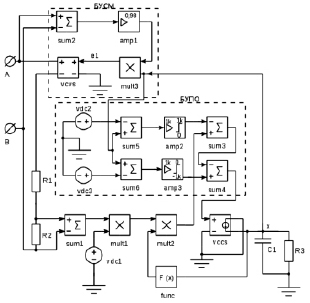
Рис. 4. Схемотехническая модель мемристора в САПР Cadence
Источник тока, управляемый напряжением vccs, преобразует выходное напряжение блока sum4 (из блока БУПО) в ток с коэффициентом преобразования, равным 1. На конденсаторе C1 этот ток интегрируется и поступает на блок умножения mult3 и блок func (для расчета функции f(x)). Напряжение на C1 численно равно значению параметра x.
В БУПО входят сумматоры (sum3, sum4, sum5, sum6) и усилители-ограничители (amp2, amp3), которые обеспечивают поддержание значений x в пределах от 0,001 до 0,999 за счет ограничительных элементов (amp2, amp3). Для выполнения функции ограничения в БУПО значения источников напряжения vdc2 и vdc3 выставляются равными 0,999В и 0,001В соответственно. Благодаря этому значение функции f(x) никогда не будет равно 0 и 1. В противном случае по достижении аргументом x крайних значений (x = [0] ∨ x = [1]) мемристор перестает управляться, так как функция f(x) (см. рис. 2) в этих точках имеет значение 0 и при умножении (в блоке mult2) результирующее напряжение будет равно нулю. Другими словами, наличие ограничивающих элементов позволяет многократно изменять состояние мемристора.
Блок БУСМ состоит из сумматора (sum2), усилителя (amp1, коэффициент 0,98), умножителя (mult3) и источника напряжения, управляемого напряжением (vcvs).
Напряжение на терминалах мемристора равно (выход sum2):
Umem= U(A) – U(B). (5)
На выходе умножителя mult3 напряжение равно
e1 = 0,98·Umem·x. (6)
Напряжение на выходе блока vcvs сокращает диапазон изменения напряжения, приложенного к резистору R1, и соответственно ток, протекающий через этот резистор, будет равен:
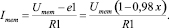 (7)
(7)
Из формулы (7) общее сопротивление мемристора равно:
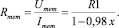 (8)
(8)
Варьируя коэффициентом усиления усилителя amp1, можно изменять сопротивление мемристора в выключенном состоянии. Во включенном состоянии Rmem = R1.
Конденсатор C1 используется в качестве элемента памяти. При снятии напряжения со входов A и B мемристора на данном конденсаторе будет сохранен заряд, который и будет определять сопротивление мемристора. Также конденсатор отражает динамические характеристики мемристора. Чем выше его емкость, тем большее время необходимо для переключения мемристора из одного состояния в другое. В схеме емкость C1 принята равной 1 мкФ.
Резистор R3 (1 ГОм) необходим для корректной работы системы моделирования и вносит поправки в динамические свойства мемристора.
Таким образом, разработанная схемотехническая модель отличается от приведенной на рис. 1 схемы механизмом преобразования величины x в сопротивление мемристора и реализуется выражением (8). Кроме того, введенные пороги ограничения позволяют многократно перепрограммировать элементы памяти, построенные на основе разработанной модели.
Результаты моделирования мемристора представлены на рис. 5.
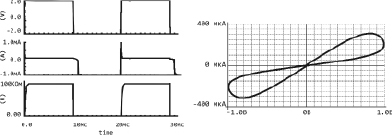
Рис. 5. Результаты моделирования схемы мемристора в САПР Cadence:
а – временная диаграмма работы мемристора (диаграмма V показывает напряжение Umem, диаграмма A - ток Imem, диаграмма R – сопротивление Rmem, рассчитанное по (8));
б – гистерезис вольт-амперной характеристики
Из диаграммы напряжения (рис. 5,а) видно, что при подаче на мемристор напряжения Umem = 2 В, мемристор переходит в состояние с высоким сопротивлением (уровень 100 кОм на диаграмме R). При подаче напряжения –2 В мемристор переключается в состояние с низким сопротивлением (уровень приблизительно 10 Ом на диаграмме R).
Разработанная модель может быть использована при проектировании интегральных схем, использующих мемристоры.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (гос. соглашение № 14.A18.21.0107) в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.
Рецензенты:
Агеев О.А., д.т.н., профессор, директор Научно-образовательного центра «Нанотехнологии» Южного федерального университета, г. Таганрог;
Рындин Е.А., д.т.н., профессор, ведущий научный сотрудник Южного научного центра Российской академии наук (ЮНЦ РАН), г. Ростов-на-Дон.
Работа поступила в редакцию 16.10.2012.
Библиографическая ссылка
Коноплев Б.Г., Ковалев А.В., Кальсков В.В., Лукьяненко Е.Б., Кальсков А.В., Комаров И.А. СХЕМОТЕХНИЧЕСКАЯ МОДЕЛЬ МЕМРИСТОРА В САПР CADENCE // Фундаментальные исследования. – 2012. – № 11-2. – С. 412-415;URL: https://fundamental-research.ru/ru/article/view?id=30548 (дата обращения: 20.04.2024).



