При исследовании надежности и долговечности деталей и узлов ковочных молотов возникает необходимость в определении действующих нагрузок.
Падающие части ковочного молота в процессе ударного взаимодействия с заготовкой можно моделировать сложной вязкоупругой стержневой системой с распределенными параметрами, соударяющейся с препятствием. Применение предлагаемого подхода позволяет производить расчет напряженно-деформированного состояния в любом интересующем сечении рабочих частей молота, а также дает возможность проводить вариантные расчеты с целью совершенствования конструкции ковочных молотов.
Для решения поставленной задачи используем частотный метод динамического расчета нестационарных колебаний ковочного молота в процессе ударного взаимодействия с заготовкой. Предлагаемая методика использует модификацию метода конечных элементов (МКЭ), основанную на точном интегрировании дифференциального уравнения для конечного элемента [2], и позволяет рассчитывать продольные и поперечные колебания стержней ступенчато-переменного сечения с учетом или без учета рассеяния энергии при соударении с жестким препятствием [3, 6].
Для учета упругого рассеяния энергии согласно Сорокину С.Е. [4] для частотно-независимого трения все характеристики упругости системы заменять комплексными величинами, в данном случае:
![]()
![]()
![]()
![]()
где γ – коэффициент сопротивления.
Для заготовки, обладающей одновременно упругостью, вязкостью и пластичностью в различных формах и соотношениях и моделируемой элементом Максвелла, учет рассеяния энергии будем осуществлять согласно [5]:
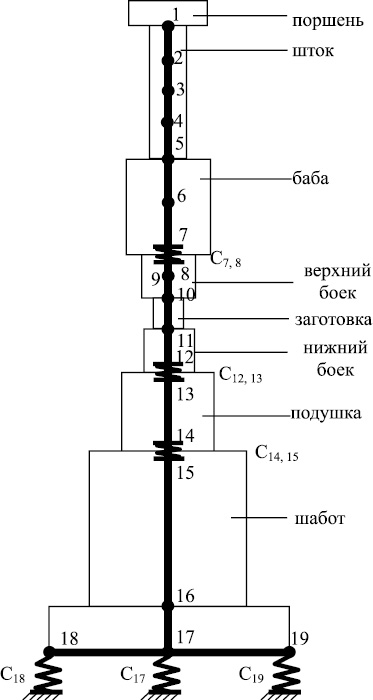
Рис. 1. Расчетная схема молота М1345:1 – 19 – узлы системы; С7, 8, С12, 13, С14, 15 – жесткости пружин
Коэффициент tM определяется экспериментальным путем.
Рассмотрим паровоздушный ковочный молот арочного типа модели М1345. Принципиальная схема молота показана на рис. 1.
Основные параметры и размеры молота М1345 приняли для расчета согласно ГОСТ 9752-75. При составлении расчетной схемы молота считалось, что в штоке, бабе, бойках, подушке и верхней части шабота возникают продольные колебания, а в основании шабота – поперечные.
Таким образом, расчетная схема ковочного молота (см. рис. 1) будет состоять из 19 узлов.
Участки 7–8, 12–13 и 14–15 моделируют стыки. Методика расчета контактных деформаций стыков с учетом реальных условий заимствована из работы [1]. Узлы 17, 18 и 19 имеют упругое основание, заменяющее влияние подкладки из дубовых брусьев. Подкладка под шаботом, состоящая из дубовых брусьев, моделируется упругим основанием с сосредоточенной жесткостью в соответствующих узлах системы. На завершающей стадии удара верхний боек считается присоединившимся к заготовке.
Предлагаемой расчетной схеме (см. рис. 1) соответствует следующая система разрешающих уравнений для построения амплитудно-фазо-частотных характеристик (АФЧХ) перемещений:
![]()
для j = 2, 3, 4, 5, 6, 9:
![]()
![]()
для j = 8, 13: ;
![]()
![]()
для j = 10, 11,12, 14, 16:
![]()
![]()
![]()
![]()
![]()
![]()
где ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где j – номер узла (i = 1,2…19); Wj – перемещение j-го узла, м; φj – угол поворота j-го узла, рад; сj – жесткости пружин, моделирующих упругое основание в j-ом узле, кг/м; сnk – жесткости пружин, моделирующих стыки nk, кг/м.
Из системы разрешающих уравнений находятся изображения перемещений U(ω) в узлах системы. Для получения переходного процесса используется дискретное преобразование Фурье. В ходе исследований выявлен информативный диапазон частот (рис. 2), позволяющих идентифицировать получаемые АФЧХ, который составил ω = (0–400) с–1.
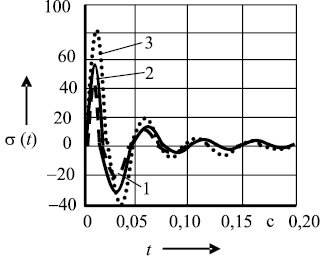
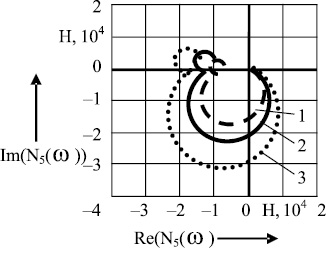
Рис. 2. Влияние скорости соударения V на напряжение σ(t) и АФЧХ усилий в 5 узле N5 (ω) заготовки из стали 45; 1, 2, 3 - соответственно V = 4, 5, 7 м/с
Теоретические исследования показали, что на напряжения, возникающие в различных узлах системы при соударении падающих частей с заготовкой, влияют скорость соударения, материал и размеры поковки (см. рис. 2).
Установлено, что максимальные напряжения, в несколько раз превышающие напряжения в других узлах системы, возникают в месте заделки штока в бабу (5 узел), что подтверждает предварительные сведения из практики о подавляющем числе поломок именно в этом сечении.
Предлагается следующий путь уменьшения нагрузок, возникающих в месте заделки штока в бабу. Можно распределить нагрузку на несколько сечений. Для этого следует в качестве новой конструкции штока использовать шток с цилиндрическими отверстиями ступенчато-переменного сечения (рис. 3). Предлагаемые изменения в конструкции штока снижают возникающие в месте заделки штока в бабу напряжения на (18–20) % и направлены на повышение надежности штоков, что позволяет увеличить срок их эксплуатации и тем самым сократить материальные потери от замены штоков и от простоя оборудования в период их замены (рис. 3).
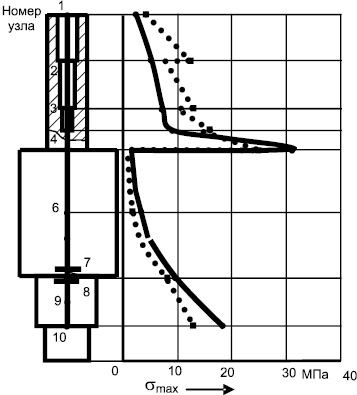
Рис. 3. Распределение напряжений в падающих частях ковочного молота: сплошная линия – для штока постоянного сечения, пунктирная линия – для штока с цилиндрическими отверстиями ступенчато-переменного сечения
Для проверки предлагаемой методики расчета ковочных молотов были проведены экспериментальные исследования в кузнечно-штамповочном производстве ЗАО «АВИАСТАР-СП» (г. Ульяновск), результаты которых показали, что средняя погрешность вычислений составляет 14 % для частот собственных колебаний и 25 % - для амплитуд колебаний(рис. 4).
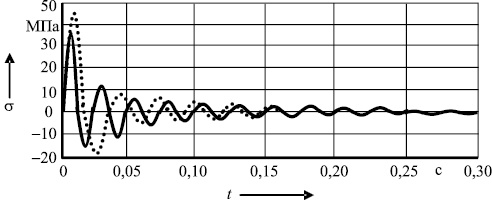
Рис. 4. Сравнение теоретических и экспериментальных амплитуд напряжений ? в месте заделки штока в бабу (заготовка – сталь 45, V = 4 м/с), где сплошная линия – экспериментальная кривая, пунктирная линия – теоретическая кривая
Применение предлагаемого подхода позволяет производить расчет напряженно-деформированного состояния в любом интересующем сечении рабочих частей молота, а также дает возможность проводить вариантные расчеты с целью совершенствования конструкции ковочных молотов.
Выводы
1. Разработана математическая модель ковочного молота для оценки ударного взаимодействия с заготовкой.
2. Найдены значения коэффициентов тела Максвелла, моделирующих заготовку при ковке.
3. Даны предложения по улучшению конструкции штока ковочного молота в виде стержня с отверстиями ступенчато-переменного сечения, повышающими его надежность при ковке.
Библиографическая ссылка
Санкин Ю.Н., Юганова Н.А. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА КОВОЧНОГО МОЛОТА // Фундаментальные исследования. – 2012. – № 11-5. – С. 1210-1213;URL: https://fundamental-research.ru/ru/article/view?id=30736 (дата обращения: 25.04.2024).



