Для того чтобы поддерживать экономику страны и не допускать возникновение в ней очередного кризиса, необходимо уметь своевременно выявлять, где и когда может «надуться пузырь», а главное, каким образом он будет сдуваться и что за этим последует. Резкий взлет и падение цен может в конечном счете привести к краху и повлечь за собой кризисный период. Первыми описанными историками и экономистами пузыри – это тюльпаномания ХVII века (Голландия) и ажиотаж вокруг Компании Южных морей в 1720-х годах (Англия). В каждый исторический период рост пузырей связан с «финансиализацией» – накоплением избыточного капитала и смещением направлений его вложения с производственной сферы в сторону финансовых рынков и спекуляций. Во многих странах мира постоянно надуваются и сдуваются «финансовые пузыри». Все это может привести к очередному кризису, и потому ежедневно аналитики анализируют рынки, дают различного рода прогнозы, пытаясь делать все возможное для предотвращения негативных последствий.
1. Сравнительный анализ моделей финансовых пузырей.
В зависимости от условий образования пузырей и их дальнейшей динамики можно выделить следующие виды пузырей.
Спекулятивные, также называемые традиционными или нерациональными, пузыри (traditional, nonrational bubbles). В данном случае актив приобретается потому, что инвестор ожидает дальнейшего роста цен, но его ожидания не основаны на объективных изменениях в фундаментальных показателях.
Рациональные пузыри. В большинстве исследований, которые основываются на теории рациональных ожиданий,[1] содержится довольно общее определение: рациональный пузырь – это разница между рыночной ценой и ценой, которая основывается на фундаментальных составляющих.
Наиболее распространен подход, когда пузырь определяется исходя из гипотезы эффективного рынка (ГЭФР). Более того, данный подход используется в большинстве рассматриваемых далее вариантах эмпирических тестов на наличие пузыря.
Рассмотрим определение доходности акции в период t + 1
![]() (1),
(1),
где r t+1 – доходность акции в будущем периоде, которая равна отношению поступлений от акции в будущем периоде, которые складываются из выплачиваемых дивидендов d t+1 и дохода от продажи акции в конце периода p t+1 за вычетом цены акции в базисном году, к стоимости акции в базисном году Pt.
Выразим текущую стоимость акции путем преобразования формулы (1):
![]() (2)
(2)
Таким образом, цена акции определяется путем дисконтирования ожидаемых денежных потоков – дивидендов и стоимости акции при продаже в будущем.
В условиях неопределенности цена акции будет зависеть от ожидаемых значений дивидендов и стоимости продажи, а также ожидаемой доходности. Для обозначения ожидаемого значения некоторого показателя исходя из всей информации, доступной в период (T – Ωt), воспользуемся показателем условного математического ожидания Et(...).[2]
Запишем формулу (2) с использованием условных математических ожиданий:
![]() (3)
(3)
Формула (3) является базовой при определении фундаментальной стоимости акций, именно с нее начинается рассмотрение пузырей на фондовом рынке в целом ряде работ, как-то: Леруа (LeRoy, 2004), Шиллер (Shiller, 1981, 2000), Уотсон (Watson, 1981), Диба, Гроссман (Diba, Grossman, 1983), Эванс (Evans, 1991).
Данная формула основывается на следующих допущениях:
– выполняется предпосылка о рациональных ожиданиях;
– отсутствие асимметричной информации;
– инвесторы нейтральны к риску;
– уровень доходности постоянен и не меняется во времени.
Следовательно, формулу (3), в которой определяется стоимость актива в момент t, можно представить с учетом вышеупомянутых требований, где доходность (r) постоянна во времени.
![]() (4)
(4)
Для последующих периодов времени можно записать уравнение (4) так:
![]() (5)
(5)
Уравнение (5) состоит из двух слагаемых: первое представляет собой сумму дисконтированных будущих дивидендов, второе – ожидаемую дисконтированную стоимость продажи акции в будущем.
В теории рациональных пузырей принято выделять составляющие цены акции следующим образом:
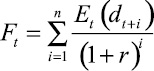 – часть цены, определяемая фундаментальными факторами;
– часть цены, определяемая фундаментальными факторами;
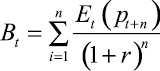 – пузырь-составляющая.
– пузырь-составляющая.
Следовательно, стоимость акции представляет собой простую сумму фундаментальной стоимости и составляющей пузыря.
Общее решение такого уравнения можно представить следующим образом:
Наблюдаемая (текущая) цена актива = фундаментальная стоимость + рациональный пузырь.
Более точно данное уравнение может быть выражено как:
Pt = Ft + Bt. (6)
Очевидно, что рациональный пузырь всегда является частью цены акции.
Если подставить выражение (6) вместо Pt в формулу (4), используя определение фундаментальной составляющей и пузыря, получим уравнение (7), которое показывает, что пузырь растет с темпом r.
![]() (7)
(7)
Рассмотрим специальный случай для уравнения (5), когда n → ∞:
![]() (8)
(8)
При устремлении n в бесконечность предел стремится к нулю, соответственно этому пузырь-составляющая исчезает, и стоимость акции в момент t определяется только динамикой дивидендов.
Уравнение (8) показывает, что текущая цена актива в любом периоде определяется текущими фундаментальными факторами данного периода и предполагаемым приростом или убытком капитала в зависимости от состояния актива до наступления следующего периода. Это отражает рациональные ожидания, так как ожидание – это математическое ожидание изменения цены актива, основанной на всей доступной в настоящее время информации [3].
Лопающиеся пузыри (collapsing bubble).
Характерной чертой лопающихся пузырей является существование вероятности «сдутия» или «схлопывания» пузыря до нулевого (или ненулевого, сколь угодно малого) уровня.
Наиболее общая и простая формула лопающегося пузыря имеет следующий вид:
![]() (9)
(9)
![]() (10)
(10)
Данные выражения имеют следующую интерпретацию: инвесторы понимают, что пузырь рано или поздно лопнет, однако они получают более высокую доходность (1 + r/π по сравнению с 1 + r) до тех пор, пока сверхвысокая доходность позволяет компенсировать риски неизбежного коллапса цен.
Внутренние пузыри (intrinsic bubble).
Внутренние пузыри формально относятся к группе рациональных пузырей. Особенностью данного вида пузырей является зависимость пузыря от размера дивидендных выплат. Если фундаментальные показатели компании стабильны и устойчивы во времени, то любая недооценённость или переоценённость акций также будет устойчива во времени, вместе с тем эта особенность приводит к излишней чувствительности цен к изменению фундаментальных показателей.
Модель образования внутренних пузырей на фондовом рынке.
Модель образования пузырей базируется на простом условии, которое связывает временной ряд реальных цен акций с временным рядом реальных дивидендных выплат при условии постоянного ожидаемого дохода.
Pt = e–r Et(Dt + P t+1 ), (11)
где Pt – реальная цена акции в начале временного периода t; Dt – реальный дивиденд на акцию за период t; r – постоянная реальная ставка процента.
Приведенная стоимость Pt будет равна
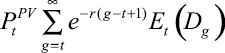 . (12)
. (12)
Предполагается, что ![]() всегда существует, так как g < r (g – темп роста дивидендов). Уравнение (12) будет единственным решением (11) при условии отсутствия пузырей:
всегда существует, так как g < r (g – темп роста дивидендов). Уравнение (12) будет единственным решением (11) при условии отсутствия пузырей:
![]() (13)
(13)
Однако уравнение (11) имеет и другие решения. Пусть ![]() – последовательность случайных переменных, такая что
– последовательность случайных переменных, такая что
![]() (14)
(14)
Внутренний пузырь строится нахождением основных параметров, которые удовлетворяют условию (14). В вышеописанной модели ценообразования единственным стохастическим фактором являются дивидендные выплаты, поэтому внутренние пузыри зависят только от дивидендов.
Предположим, что логарифм дивидендных выплат представляет собой класс случайных последовательностей, называемых мартингалом:
![]() (15)
(15)
где μ – темп роста дивидендов, dt = ln Dt в момент времени t, ![]() – нормальная случайная величина. Из уравнения (14) и предположения, что дивиденды за период t известны, когда устанавливается цена Pt, следует, что приведенная стоимость цены акции в уравнении (12) прямо пропорциональна дивидендам:
– нормальная случайная величина. Из уравнения (14) и предположения, что дивиденды за период t известны, когда устанавливается цена Pt, следует, что приведенная стоимость цены акции в уравнении (12) прямо пропорциональна дивидендам:
![]() (16)
(16)
где ![]()
(Уравнение (16) является стохастической версией модели Гордона).
Определим функцию B(D)i как
![]() (17)
(17)
где λ является положительным корнем квадратного уравнения ![]() с = const. Уравнение (17) удовлетворяет уравнению (14). Суммируя приведенную стоимость цены в уравнении (12) и пузыря в уравнении (17), получаем основное уравнение ценообразования
с = const. Уравнение (17) удовлетворяет уравнению (14). Суммируя приведенную стоимость цены в уравнении (12) и пузыря в уравнении (17), получаем основное уравнение ценообразования
![]() (18)
(18)
Уравнение (17) содержит пузырь (для с ≠ 0) и, тем самым, нарушает условие (13), цена P(Dt) является функцией только от дивидендов и не зависит от времени или от других посторонних переменных, поэтому B(Dt) является примером внутреннего пузыря.
Таким образом, внутренние пузыри отражают следующую идею: цены акций чрезмерно реагируют на новости относительно дивидендных выплат. Следовательно, когда изменяются дивиденды, цены меняются сильнее, чем в формуле приведенной стоимости. Внутренние пузыри позволяют ценам акций приближаться к уровню приведенной стоимости и потом отклоняться от нее. Хотя также возможны и произвольные большие отклонения. Различные траектории параметров могут производить резко отличающиеся траектории внутренних пузырей. Внутренние пузыри основаны на самореализующихся ожиданиях. Вместо того чтобы изменяться под воздействием внешних переменных, эти ожидания изменяются под воздействием нелинейных форм цены.
В связи с вышеизложенным присутствие пузырей на финансовых рынках позволяет объяснить волатильность цен на акции, и существует возможность некоторого прогнозирования.
2. Авторская модель идентификации периодов спекулятивного роста.
Представим авторскую точку зрения на возможность прогнозирования финансовых пузырей. Разработаем нейросетевую технологию идентификации периодов спекулятивного роста на финансовом рынке. Данная технология будет основана на перспективном направлении искусственного интеллекта – распознавании образов. Распознавание образов предполагает распознавание фигур (финансовых пузырей) на графиках с помощью однослойного перцептрона.
Функцию, реализуемую перцептроном, можно записать так:
![]()
где wi, Vn – коэффициенты; θAn, θR – пороги активации; Si – элементы упорядоченного множества; wi , Vn, θAn, θR – подбираются до тех пор, пока f(S) = 1.
На основе однослойного перцептрона с пороговой активацией разработаем инновационную вычислительную систему для прогнозирования финансовых временных рядов. В качестве примера приведем временной ряд цены на золото. Данные взяты за 1995–2012 гг. Представлены данные по месяцам.
Верным признаком того, что золото – пузырь, является непрекращающийся спрос на золото (рисунок). Точкой на графике показан момент выхода с рынка. Данный параметр сигнализирует, что пузырь есть и он должен скоро сдуться.
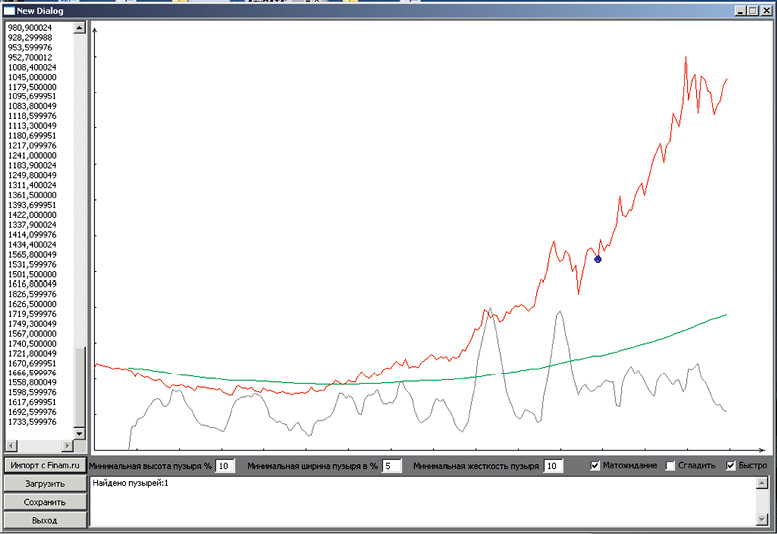
Авторская модель идентификации спекулятивного роста
Заключение
Таким образом, в статье проведен сравнительный анализ методов идентификации периодов спекулятивного роста. Предложена авторская модель определения «финансового пузыря». На базе данной модели разработана интеллектуальная система предупреждения периодов спекулятивного роста на финансовых рынках. Данная система была протестирована на выявление «финансовых пузырей» в мировой экономике.
Cтатья подготовлена по результатам исследований, выполненных за счет бюджетных средств по Государственному заданию Финуниверситета 2012 года (утверждено Министром РФ – Руководителем Аппарата Правительства РФ 03.02.2012 г. № 432п-П17). Поддержано грантом РФФИ 11-06-00278-а.
Рецензенты:
Цвиркун А.Д., д.т.н., профессор, зав. лаб. № 33 ИПУ РАН им. Трапезникова, г. Москва;
Рубцов Б.Б., д.э.н., профессор, зав. каф. «Финансовые рынки и финансовый инжиниринг», Финансовый университет при правительстве РФ, г. Москва.
Работа поступила в редакцию 13.11.2012.
Библиографическая ссылка
Иванюк В.А., Станик Н.А., Попов В.Ю. СРАВНИТЕЛЬНЫЙ АНАЛИЗ МОДЕЛЕЙ И МЕТОДОВ ФИНАНСОВЫХ ПУЗЫРЕЙ // Фундаментальные исследования. – 2012. – № 11-5. – С. 1261-1265;URL: https://fundamental-research.ru/ru/article/view?id=30747 (дата обращения: 20.04.2024).



