В газовой, нефтеперерабатывающей и нефтехимической промышленности широкое применение находят трубчатые печи. Основные элементы конструкций современных высокотемпературных трубчатых печей (пиролиза, конверсии, риформинга и прочих) работают на пределе возможностей конструкционных материалов. Погрешность в оценке локальных значений тепловых потоков, скорости продуктов сгорания в пристеночном слое, температуры стенки труб и футеровки в лучшем случае значительно удорожает, а в худшем - существенно снижает срок службы печи. Имеются печи с беспламенными горелками на излучающих стенах, с горелками настильного и открытого сжигания газообразного топлива. Рассматриваемые в данной работе трубчатые печи характеризуются малой шириной радиационной камеры по сравнению с ее длиной и высотой, симметричным расположением трубчатого экрана и ряда горелок. В этом случае изменение параметров потока по длине намного меньше, чем по ее ширине и высоте. Поэтому задачу теплообмена и газовой динамики продуктов сгорания можно рассматривать в двухмерной постановке. Малый диаметр труб реакционного змеевика по сравнению с размерами камеры радиации и малый шаг между ними позволяет рассматривать трубчатый экран как твердую лучевопринимающую стенку, что также упрощает решение газодинамической задачи. В случае настильного сжигания топлива и использования беспламенных горелок имеет место косвенный направленный режим теплообмена.

Рис. 1. Расположение веерных горелок в два яруса
Разработанный нами дифференциальный метод расчета внешнего теплообмена в трубчатых печах [1–4] здесь используется для моделирования печей с газовыми веерными горелками настильного пламени. Газовые веерные горелки типа ГВН предназначены для сжигания газового топлива в трубчатых печах для замены панельных беспламенных горелок типа ГБПш. Упрощенная схема расположения горелок показана на рис. 1.
Конструкция выходной раздаточной головки обеспечивает высокую равномерность разогрева поверхности настила прямоугольной формы площадью 1,5-1,8 м2 при соотношении сторон от 2:1 до 4:1. Факелы горелок настилаются на стены, выложенные из огнеупорного кирпича.
Первичный воздух поступает в инжекционный смеситель, далее газовоздушная смесь с коэффициентом избытка воздуха 0,65-0,75 через каналы в выходной головке распределяется по поверхности настила. Вторичный воздух поступает через кольцевой канал благодаря разрежению в топке и эжектирующему эффекту настильного факела.
Дифференциальный метод теплового расчета топок основан на совместном численном интегрировании двухмерных уравнений переноса излучения (1), энергии (2), турбулентного движения продуктов сгорания (3), двухпараметрической k-e модели турбулентности (4), неразрывности (5), модели горения (6):
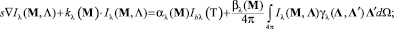 (1)
(1)
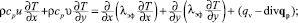 (2)
(2)
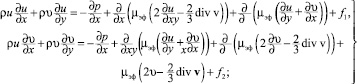 (3)
(3)
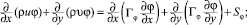 (4)
(4)
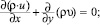
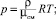 (5)
(5)
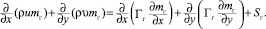 (6)
(6)
В этих уравнениях Il(M,Λ) - спектральная интенсивность излучения в точке М в направлении Λ; Ibl(T) - спектральная интенсивность излучения черного тела при температуре Т; kl(M) = al + bl - спектральный коэффициент ослабления; al(M), bl(M) - спектральные коэффициенты поглощения и рассеяния; gl(Λ,Λ′) - индикатриса рассеяния; u, u - компоненты скорости продуктов сгорания вдоль осей х и у; ср - изобарная теплоемкость; lэф = l + lт - коэффициент эффективной теплопроводности; qv - объемная плотность источников тепла; div qp - мощность плотности лучистых потоков; mэф = m + mт - эффективная вязкость; k, e - кинетическая энергия турбулентных пульсаций и скорость ее диссипации; f = {k, e}; Гf = m + mт/sf - коэффициент переноса; Sf - источниковый член; mг, mок массовые концентрации горючего и окислителя; Sг - скорость химической реакции; Гг = m/sг - коэффициент переноса, где sг - число Шмидта.
а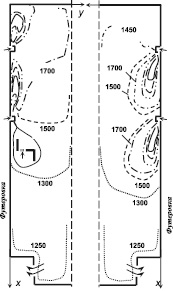 б
б
Рис. 2. Изотермы при разных направлениях пламени: а – поток вверх; б – поток вниз; 2000К; 1900К; 1800К
Эффективную степень черноты eэфl и отражательную способность rэфl трубчатого экрана можно вычислить по формулам [5]:
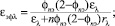
rэфl = 1 - eэфl, (7)
где el, rl - спектральная степень черноты и отражательная способность наружной поверхности труб; jпэ - угловой коэффициент, зависящий от расстояния между трубами (шага) Sэ и внешнего диаметра труб.
Система координат, область интегрирования и изотермы в камере радиации в случае направления настилающихся факелов вверх и вниз показана на рис. 2.
Система уравнений (2)–(6) дополняется граничными условиями. На входном участке для уравнения энергии, уравнений движения, уравнений модели турбулентности, модели горения ставится граничное условие 1 рода. Для уравнений движения на твердой границе ставятся условия прилипания и непроницаемости. На жесткой стенке для уравнений модели горения задается условие отсутствия потока. Для уравнения энергии на жесткой стенке ставятся граничные условия 1 или 3 рода. На выходе из топки задается условие нулевого градиента. На твердой границе диффузионный поток кинетической энергии турбулентности полагается равным нулю.
При использовании метода дискретных ординат уравнение переноса излучения (1) заменяется системой дифференциальных уравнений относительно интенсивности излучения 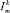 вдоль ограниченного количества выделенных направлений Sm {Sm; m = 1, No}. Эти направления задаются набором угловых координат {mm, xm; m = 1, No}, равные величине проекции единичного вектора направления Sm на оси координат 0х и 0у соответственно. В зависимости от их количества различают S2 - приближение (No = 4), S4 - приближение (No = 12), и другие [6]. Вместо интегро-дифференциального уравнения получается система дифференциальных уравнений относительно интенсивности излучения в k-м спектральном диапазоне вдоль каждого из этих направлений m:
вдоль ограниченного количества выделенных направлений Sm {Sm; m = 1, No}. Эти направления задаются набором угловых координат {mm, xm; m = 1, No}, равные величине проекции единичного вектора направления Sm на оси координат 0х и 0у соответственно. В зависимости от их количества различают S2 - приближение (No = 4), S4 - приближение (No = 12), и другие [6]. Вместо интегро-дифференциального уравнения получается система дифференциальных уравнений относительно интенсивности излучения в k-м спектральном диапазоне вдоль каждого из этих направлений m:
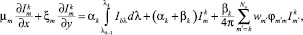 (8)
(8)
где ak, bk - осредненные спектральные коэффициенты поглощения и рассеяния в определенном спектральном диапазоне k; mm, xm - угловые координаты и wm - весовые коэффициенты [6].
Для численного решения дифференциальных уравнений метода дискретных ординат (8) совместно с граничными условиями применяется конечно-разностный метод [2, 3].
Для алгебраической аппроксимации уравнений (2)–(6) применена разностная сетка «шахматного» типа. Узлы, в которых определяются продольная u и поперечная u составляющие скорости, сдвинуты относительно «основных» узлов на полшага в продольном и поперечном направлениях соответственно.
Исследования закономерностей теплообмена и аэродинамики топочных газов при настильном сжигании топлива выполнены на примере трубчатой печи водяной конверсии природного газа. Камера радиации указанной печи состоит из двух секций, расположенных симметрично относительно однорядного трубчатого змеевика с вертикальным расположением труб. Количество труб в змеевике 28, диаметр 134×12 мм, шаг 300 мм, обогреваемая длина труб 10 м. В численных исследованиях были рассмотрены разные возможные варианты расположения горелок и направления пламени.
Состав топливного газа (в % об): Н2 - 52,0; СН4 - 25,0; С2Н6 - 8,74; С3Н8 - 6,5; С4Н10 - 6,0; С5Н12 - 1,3; N2 - 0,4; СО2 - 0,03; СО - 0,03. Расход топливного газа в камеру радиации Вт = 0,4 нм3/с, низшая теплота сгорания 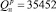 кДж/нм3, температура топливной смеси на входе в горелки 493 К, температура воздуха, подаваемого в горелки, 453 К. Коэффициент избытка воздуха aт = 1,1. Расчеты выполнены при равномерном распределении топливного газа по ярусам горелок.
кДж/нм3, температура топливной смеси на входе в горелки 493 К, температура воздуха, подаваемого в горелки, 453 К. Коэффициент избытка воздуха aт = 1,1. Расчеты выполнены при равномерном распределении топливного газа по ярусам горелок.
Лучистый теплообмен рассматривался в S2 -приближении метода дискретных ординат. Учитывалась зависимость теплофизических и оптических, свойств продуктов сгорания от температуры.
При двухмерном моделировании работы веерных горелок приняты упрощения: предполагается, что смесь газа с первичным воздухом поступает в печь в направлении оси х через узкую щель со скоростью 16,2 м/с, вторичный воздух через две щели, расположенные с двух сторон относительно щели для газа поступает со скоростью 2,2 м/с. Схема подачи газа и воздуха в печь в несколько укрупненном виде показана внутри рис. 2.
Эффективная степень черноты поверхности нагрева, определенная по формуле (7), равна 0,79. Температура наружной поверхности труб линейно менялась от 1150 к до 1200 К. Предполагается, что твердые поверхности диффузно испускают собственное и отражают падающее излучение. Степень черноты футерованных боковых стенок e = 0,42, коэффициент теплопроводности с учетом многослойности стенок l = 0,35 Вт/(м×К). Учитывалась потеря теплоты через стенки за счет теплопроводности. Наружная температура стенок печи принята равной 300 К. Толщина стенок 0,45 м. Степень черноты свода и пода принята равной 0,67.
На рис. 3 показан вид линий тока y в объеме топки при направлении настилающих факелов вверх (левая половина) и вниз (правая половина). На рис. 4 представлены поперечные профили продольной скорости газов u выше верхнего яруса горелок на разных расстояниях х от свода печи.
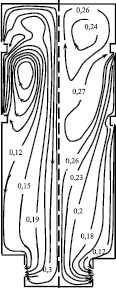
Рис. 3. Вид линий тока y
При расположении веерных горелок настильного пламени на боковых стенах камеры радиации аэродинамическая картина течения продуктов сгорания и пространственное распределение тепловых характеристик становятся более сложными. Поле течения можно разделить на две зоны: прямого и обратного токов. Зона прямого тока расположена в непосредственной близости от настильной стены и характеризуется относительно большими значениями скорости движения и температуры продуктов сгорания. В случае направления факелов вниз зона обратного тока расположена вблизи поверхности нагрева в верхней части печи. При направлении факелов вверх зоны обратного тока расположены ближе к горелкам, а трубчатые реакторы в основном омываются потоками горячих продуктов сгорания. При направлении факелов вниз существенно изменяется характер омывания трубчатого экрана продуктами сгорания. Вблизи поверхности нагрева на уровне между ярусами горелок происходит торможение течения.
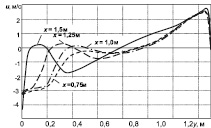
Рис. 4. Поперечные профили скорости газов в верхней части печи на разных расстояниях х от свода
На рис. 5 приведены распределения поверхностных плотностей суммарных, лучистых и конвективных тепловых потоков при сводовом расположении диффузионных горелок и при двух вариантах направления факелов от веерных горелок. При сводовом режиме сжигания газа распределение поверхностных плотностей тепловых потоков по длине трубчатого экрана имеет характерный максимум в области пламени и достаточно быстрое убывание потоков вниз по течению. При использовании веерных горелок с направлением пламени вверх распределение лучистых потоков более плавно убывает по всей длине труб.
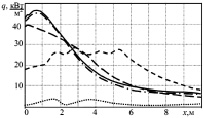
Рис. 5. Распределение плотностей тепловых потоков по длине труб при разных режимах сжигания топлива: суммарных тепловых потоков при сводовом; лучистых тепловых потоков при сводовом сжигании; лучистых потоков при веерных горелках, поток вверх; лучистых потоков при веерных горелках, поток вниз; конвективных тепловых потоков
При направлении продуктов сгорания вверх в направлении свода камеры зоны обратного тока, как это видно из рис. 3, вытесняются ближе к футерованной боковой стенке. В этом случае поверхность нагрева по всей длине реакционных труб омывается горячими продуктами сгорания от факелов по ходу прямого тока. Такой характер движения дымовых газов оказывает существенное влияние на распределение температуры продуктов сгорания в объеме камеры радиации. Поле температуры в топках трубчатых печей в основном формируется лучистым переносом энергии. Как видно из рис. 2, при направлении факелов вверх вся верхняя часть камеры радиации, включая области около труб, заполнена продуктами сгорания с высокой температурой. В то же время при расположении горелок на своде свод омывается газами обратного тока с более низкой температурой. Когда факелы настилаются вверх, на высоте печи по оси х от 2 до 6 м наблюдается увеличение как лучистой, так и конвективной составляющей теплового потока к поверхности нагрева. В этом случае доля конвективной составляющей в суммарном тепловом балансе составляет до 9 %.
Как можно видеть из рис. 5, распределение плотностей лучистых тепловых потоков по длине труб при направлении факелов вниз значительно отличается от соответствующих распределений для двух первых вариантов. Можно заметить более низкие значения плотностей лучистых потоков в верхней части печи с постепенным увеличением их в середине камеры. Можно обратить внимание на наличие нескольких небольших максимумов в распределении, что объясняется двухъярусным расположением горелок и наличием максимумов в распределении конвективных потоков. Однако в этом случае доля конвективной составляющей в общем тепловом балансе меньше 3,5 %. Распределение плотностей тепловых потоков по длине труб при направлении настилающих факелов вниз получается более равномерным. При этом суммарная теплоотдача в камере радиации уменьшается до 5 % и несколько возрастает температура продуктов сгорания, покидающих камеру радиации. Правда, при расположении настилающих горелок ближе к своду все три варианта сжигания топлива обеспечивают практически одинаковую суммарную теплоотдачу.
Выводы
В работе показана возможность теплового расчета технологических трубчатых печей с газовыми веерными горелками настильного пламени в рамках дифференциального метода расчета топок. Оптимальным с точки зрения наибольшей теплоотдачи является направление настилающихся факелов вверх и расположение ярусов горелок вблизи свода камеры радиации. В то же время при направлении факелов вниз получается более равномерное распределение тепловых потоков по длине труб. При использовании горелок с настилающимися факелами потери тепла через боковые стенки труб составляют до 3 %, что несколько выше, чем при расположении горелок на своде.
Рецензенты:
Шигапов А.Б., д.т.н., профессор кафедры газотурбинных установок и двигателей ФГБОУ ВПО «Казанский государственный энергетический университет», г. Казань;
Липаев А.А. д.т.н., профессор кафедры разработки и эксплуатации нефтяных и газовых месторождений ФГБОУ ВПО «Удмуртский государственный университет», г. Ижевск.
Работа поступила в редакцию 06.03.2013.
Библиографическая ссылка
Вафин Д.Б., Садыкова Д.А. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО МЕТОДА ТЕПЛОВОГО РАСЧЕТА ДЛЯ ТРУБЧАТЫХ ПЕЧЕЙ С ВЕЕРНЫМИ ГОРЕЛКАМИ НАСТИЛЬНОГО ПЛАМЕНИ // Фундаментальные исследования. – 2013. – № 6-1. – С. 13-18;URL: https://fundamental-research.ru/ru/article/view?id=31406 (дата обращения: 16.04.2024).



