Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Патрушева Т.В. 1 Патрушев Е.М. 1

---

1 ФГБОУ ВПО «Алтайский государственный технический университет им. И.И. Ползунова»

В статье рассматривается пример использования генератора хаотических колебаний в качестве обнаружителя слабых периодических сигналов на фоне преобладающих шумов. Предлагается полученный сигнал, содержащий шум, и полезный сигнал подавать в неавтономный генератор хаоса. Изначально параметры генератора хаоса должны быть подобраны таким образом, чтобы обеспечить близость рабочей точки к границе периодического и хаотического режимов. Рекомендовано в качестве границы режимов использовать касательную бифуркацию, при которой возникновение хаоса происходит через перемежаемость. По установившемуся виду движения в системе (хаотическому или периодическому) можно судить о факте обнаружения сигнала. Распознавание вида движения в хаотическом генераторе осуществляется по виду спектра сигнала на его выходе. Авторами получены параметры бифуркационных границ и количественно исследована способность к обнаружению сигналов на фоне шумов. Предложенный способ апробирован на лабораторном макете фотоэлектрического датчика диффузного типа.

Статья в формате PDF

470 KB

фотоэлектрический датчик

генератор хаоса

шум

бифуркации

перемежаемость

обнаружитель слабых сигналов

1. Домбровский А.Н., Решетняк С.А. О стохастической фильтрации сигналов в нелинейных электрических системах //Радиотехника и электроника. – 2009. – Т.54, № 11. – С. 1369–1371.

2. Лысенко О. Фотоэлектрические датчики компании Sick AG //Электронные компоненты. – 2005. – № 5. – М.:ИД. «Электроника». – С. 8–10.

3. Патрушева Т.В. Амплитудный измерительный преобразователь на основе генератора хаоса / Т.В. Патрушева, Е.М. Патрушев // Технические науки – от теории к практике. – Т. 38. – Новосибирск : Сибирская ассоциация консультантов, 2012. – С. 104–109.

4. Патрушева Т.В. Выбор оптимальных режимов работы амплитудного измерительного преобразователя на основе генератора хаоса // Ползуновский альманах. – Барнаул, 2012. – № 2. – С. 104–107.

5. Патрушева Т.В. Обнаружение слабых периодических сигналов на фоне шумов в приборах контроля, основанных на использовании генератора хаоса / Т.В. Патрушева, Е.М. Патрушев // Измерение, контроль, информатизация: материалы Четырнадцатой междунар. науч.-техн. конф. – Барнаул: Изд-во АлтГТУ, 2013. – С. 46–51.

6. Chen H.Y. Chaos weak signal detecting algorithm and its application in the ultrasonic Doppler bloodstream speed measuring // J. Phys. Conf. Ser.13., London : IOP Publishing. – 2005. – Р. 320–324.

7. Murali, K. The simplest dissipative nonautonomous chaotic circuit, Trans. Circuits Syst. – New York: Circuits and Systems Society, 1994. – Vol. 41. – Р. 462–463.

В настоящее время выпускается большое разнообразие фотоэлектрических датчиков, предназначенных для средств автоматизации. Условия эксплуатации таких датчиков в промышленном производстве могут быть тяжёлыми. К тяжёлым факторам относятся следующие: вибрации и промышленные шумы, высокая запылённость, большие расстояния до контролируемого объекта [2]. Применительно к схемотехнике датчика эти факторы приводят к ухудшению отношения сигнал/шум (SNR) на входе устройства и требуют использования методов выделения сигналов на фоне помех.

Для решения подобных технических задач существуют разнообразные подходы, состоящие в особой схемной обработке основного рабочего сигнала датчика вплоть до применения цифровых сигнальных процессоров. Среди известных методов линейной обработки сигнала на фоне шумов отметим согласованную фильтрацию и корреляционный приём. Тем не менее задача выделения слабых сигналов на фоне преобладающих шумов остаётся актуальной, получая решения на основе нелинейных радиотехнических систем, в том числе и демонстрирующих хаос [1].

Одним из направлений исследования в области детерминированного хаоса является разработка методов использования хаотических генераторных режимов для нужд измерительной техники. В [6] описывается измерительный преобразователь допплеровского расходомера на основе генератора хаоса, работающий в условиях слабого полезного сигнала. Сообщается, что обнаружение полезного сигнала возможно при SNR до минус 26 дБ.

Цели и методы исследования

1. Выполнить анализ особенностей реализации режимов сложных колебаний в нелинейных осцилляторах.

2. Осуществить численное моделирование и исследование режимов работы различных вариантов построения датчиков, основанных на использовании бифуркаций в генераторах хаотических колебаний.

3. Разработать опытный образец датчика контроля на основе генератора хаоса и провести его испытания в лабораторных условиях.

В работе использованы методы теории колебаний, методы качественного анализа динамики нелинейных систем, теории электрических цепей, методы математической статистики и обработки экспериментальных данных.

Теоретическое обоснование

Рассмотрим принцип работы бифуркационного функционального преобразователя. Его основу составляет неавтономная система, демонстрирующая хаотическое поведение. Параметры системы подбираются таким образом, чтобы обеспечить близость к границе периодического и хаотического режимов, на которой возникает хаос через перемежаемость.

Важным свойством рождения хаоса через перемежаемость является жёсткое изменение динамики движения системы в целом и изменение чувствительности траектории к начальным условиям или небольшим её отклонениям при незначительном изменении одного из параметров. Так, если движение хаотическое, то небольшие отклонения будут приводить к усложнению траектории, то есть действие шумового сигнала на систему в хаотическом режиме будет приводить к увеличению стохастичности движения. В докритическом режиме периодических колебаний старший показатель Ляпунова становится отрицательным, то есть периодическая траектория становится устойчивой к шумоподобным отклонениям, сохраняя свою периодичность. Выбор данной критической точки в качестве основной для создания бифуркационного варианта измерительного преобразователя должен обеспечить способность к обнаружению слабых на фоне шумов сигналов и стать шагом к созданию датчиков с помехоустойчивостью на физическом уровне.

За основу может быть взята практически любая неавтономная система, демонстрирующая хаотическое поведение. Одним из представителей семейства Чуа является неавтономный генератор Murali – Lakshmanan – Chua, получивший название MLC–цепь [7]. MLC–цепь топологически проста, имеет два реактивных элемента и один нелинейный элемент с кусочно-линейной характеристикой, имеется опорный генератор, относительно которого легко анализировать состояния этой цепи (рис. 1).

Для MLC‒цепи можно записать систему уравнений в безразмерных величинах 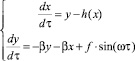(1):

(1)

где x, y – обобщённые координаты системы; τ – безразмерное время; f – амплитуда опорного генератора; ω – безразмерная частота опорного генератора; h(x) – функция нелинейного преобразования элемента g, описываемая следующим выражением:

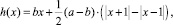
где a = –1,02; b = –0,55; β – бифуркационный параметр системы, определяемый через элементы электрической схемы (см. рис. 1):

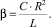
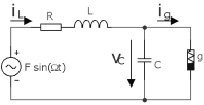
Рис. 1. MLC-цепь

При определённых величинах β и ω амплитуда опорного генератора f фиксируется вблизи некоторого критического значения fкр, соответствующего бифуркационной точке.

Создание расчётной модели

Хаотическая MLC‒цепь, в которую подается обнаруживаемый сигнал dsin ωτ в присутствии шумовой помехи, может быть описана следующим уравнением:

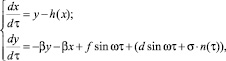(2)

где n(τ) – гауссовский случайный процесс, с нулевым средним значением, равномерным, частотно ограниченным спектром, действующим значением, равном 1.

Кроме настройки генератора хаоса близко к точке бифуркации, также необходимо определить допустимые величины для обнаруживаемого сигнала и уровня шума, сопровождающего его. Если окажется, что мощность помехи превысит некоторое значение, то это приведёт к тому, что периодический режим, несмотря на свою устойчивость, будет разрушен. Также, если амплитуда обнаруживаемого сигнала окажется недостаточной для перехода в другой режим, то не удастся воспользоваться достоинствами бифуркационного подхода.

Теоретический подбор указанных величин возможен лишь с применением методов численного моделирования, который был выполнен в Matlab/Simulink (рис. 2).

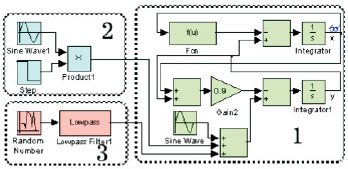
Рис. 2. Расчётная модель в Matlab/Simulink для решения уравнения (2). Цифрами обозначены: 1 – MLC‒цепь; 2 – источник обнаруживаемого сигнала; 3 – источник шума

Моделирование позволило найти наиболее подходящие значения для частоты ω и бифуркационого параметра β в безразмерных величинах. В работе [4] среди прочих были рекомендованы значения β = 0,9; ω = 0,4; fкр = 0,08245. Амплитуда опорного генератора f должна быть задана несколько меньше fкр, таким образом, чтобы при поступлении на вход обнаруживаемого сигнала dsin ωτ происходил бы переход из хаотического режима в периодический. Численные эксперименты позволили установить надёжное переключение режимов при надкритичности. составляющей не менее 0,1 %, а докритичности 1–2 % от fкр. С использованием модели частотно-ограниченного генератора белого шума были установлены возможности обнаружения сигналов на фоне преобладающих шумов генератором хаоса. Ширина полосы частот B генератора шума задавалась относительно частоты опорного генератора ν = ω/(2π) таким образом, чтобы провести исследования при B/ν, принимающем значения от 2 до 50. Удалось установить способность к обнаружению для B/ν = 2 при SNR = –16 дБ, а для B/ν = 50 при SNR = –28 дБ, что было подтверждено физическим экспериментом [3].

Применением масштабных множителей к уравнению (2) можно пересчитать параметры системы для любых частот, напряжений и токов. Возможность практического применения обнаружителя слабых на фоне шумов сигналов была рассмотрена на примере фотоэлектрического датчика диффузного типа. Действительно, работа фотоэлектрического датчика в производственных условиях нередко может быть осложнена повышенной запылённостью среды или слабой отражательной способностью контролируемого объекта. В случае, если мощность источника излучения невелика, получаемый на входе фотоприёмника сигнал будет весьма слаб, что в результате предварительного усиления потребует применения обнаружителя.

Структурная схема практической реализации приведена на рис. 3.

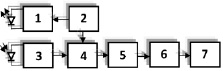
Рис. 3. Структурная схема фотоэлектрического датчика диффузного типа. Цифрами обозначены: 1 – драйвер светодиода; 2 – генератор синусоидальный; 3 – усилитель фотоприёмника; 4 – генератор хаоса; 5 – фильтр; 6 – детектор; 7 – компаратор

Основу устройства составляет синусоидальный генератор частотой 10кГц, управляющий светодиодом и одновременно являющийся задающим для генератора хаоса. Получаемый фотодиодом отражённый сигнал усиливается с применением частотной коррекции и подаётся в генератор хаоса. Установившийся режим генератора хаоса является основным выходным параметром обнаружителя. Для диагностирования хаоса применён ФНЧ с частотой среза, не превышающей ω/3, поскольку хаотический режим характерен наличием турбулентных выбросов, приводящих к появлению в спектре большого числа низкочастотных составляющих. Затем отфильтрованный сигнал детектируется и подаётся на вход компаратора, где сравнивается с некоторой величиной. Порог сравнения устанавливается из соображения максимальной вероятности обнаружения при заданной вероятности ложной тревоги [5]. Время обнаружения определяется постоянной времени детектора.

Макет датчика, представленный на рис. 4, был испытан в лабораторных условиях в течение 30 дней, полученные технические характеристики приведены в таблице.

Рис. 4. Внешний вид лабораторного макета фотоэлектрического датчика

Основные технические характеристики фотоэлектрического датчика диффузного типа на основе генератора хаоса

Выводы

Использование генератора хаоса в качестве измерительного преобразователя возможно там, где требуется осуществить обнаружение периодического сигнала на фоне преобладающих шумов.

Рассмотрена возможность использования неавтономного генератора хаоса в качестве обнаружителя сигналов на примере MLC‒цепи. Определены наиболее подходящие параметры системы, необходимые для работы генератора хаоса в качестве обнаружителя сигналов.

Способность хаотического генератора к обнаружению периодических сигналов на фоне шумов сильно варьируется в зависимости от ширины полосы частот шума и SNR. В случаях, когда SNR становится меньше некоторого значения, способность к обнаружению резко падает даже при задании любого, сколь угодно большого интервала времени обнаружения. Причиной этого является ограниченная способность генератора сохранять периодический режим под внешним шумовым воздействием, следовательно, мощность шумовой помехи на входе обнаружителя не должна превышать некоторого значения.

Макет фотоэлектрического датчика на основе генератора хаоса экспонировался на выставке «Мир, Человек, Измерения – 2013» в Барнауле и был удостоен Серебряной медали.

Рецензенты:

Суторихин И.А., д.т.н., профессор, главный научный сотрудник лаборатории гидрологии и информатики Института водных и экологических проблем Сибирского отделения Российской академии наук, ФГБУН ИВЭП СО РАН, г. Барнаул;

Тищенко А.И., д.т.н., профессор кафедры «Общая электротехника и автоматизированный электропривод», ФГБОУ ВПО «Алтайский государственный технический университет им. И.И. Ползунова», г. Барнаул.

Работа поступила в редакцию 03.06.2013.

Библиографическая ссылка