Отдельные виды суспензий при соответствующих размерах и концентрации мелкодисперсных частиц демонстрируют особенности реологического поведения [4–8]. С точки зрения зависимости эффективной вязкости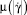 
от скорости сдвига 
эти особенности сводятся к следующему. Приближение скорости сдвига к некоторому конечному по величине, критическому значению 
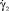крутизна S кривой течения для зависимости касательного напряжения τ от 
начинает неограниченно возрастать. На модельном уровне можно полагать, что 
. Поскольку S напрямую характеризует вязкие свойства жидкости, такое поведение суспензий можно интерпретировать как проявление эффекта «упрочнения» или «отвердевания». Также отметим, что отдельные виды таких суспензий [4, 7, 8] демонстрируют немонотонный характер поведения функции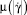 
. На начальном интервале изменения скорости сдвига от нуля до некоторого порогового значения 
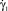функция 
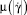монотонно убывает, и жидкость демонстрирует псевдопластическое поведение с некоторыми значениями коэффициента консистенции K1 и индекса течения n1. Дальнейшее же увеличение модуля скорости сдвига на интервале 
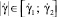после прохождения точки минимума приводит к возрастанию эффективной вязкости. При этом жидкость соответственно демонстрирует дилатантное поведение.
В работе [1] предложена реологическая модель, описывающая механическое поведение подобных неньютоновских жидкостей, а в [2] для такой модели рассмотрена задача об установившемся напорном течении в цилиндрическом канале радиуса R. Там же показано, что в зависимости от величины перепада давления Δp на длине канала L возможны три различные схемы течения.
Если перепад давления не превышает некоторого порогового значения Δp1, т.е выполняется условие
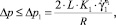(1)
то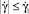 
, и всюду внутри канала суспензия демонстрирует псевдопластическое поведение. Такая схема течения условно называется первой схемой течения.
Вторая схема течения имеет место в случае, когда выполняется условие
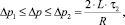
где τ2 – константа реологической модели суспензии, представляющая собой предельное значение касательного напряжения, достигаемого при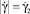 
. Для второй схемы течения характерным является то, что в канале можно выделить две зоны течения. В первой зоне жидкость по-прежнему демонстрирует псевдопластическое поведение, а во второй проявляет дилатантные свойства. Граница раздела между этими зонами представляет собой цилиндрическую поверхность некоторого радиуса Rμ1 < R. Естественно, что на этой границе должно выполняться условие 
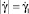. При этом первая зона в поперечном сечении канала занимает область в форме круга радиуса Rμ1, а вторая зона – кольцо Rμ1 < r < R .
Третья схема течения отличается от двух предыдущих тем, что в окрестности стенки канала формируется третья зона, заполненная материалом «отвердевшей» жидкости. Граница раздела второй и третьей зон представляет собой цилиндрическую поверхность некоторого радиуса Rμ2, который удовлетворяет условию Rμ1 < Rμ2 < R.
Рассмотрим задачу о конвективном теплопереносе в цилиндрическом канале неньютоновской жидкости рассматриваемого типа с учетом диссипации механической энергии для первой схемы течения в случае, когда выполняется условие (1). Будем предполагать, что на стенках канала для температуры выполняются граничные условия первого рода.
Введем цилиндрическую систему координат традиционным образом. Уравнение конвективного теплопереноса [3] в цилиндрическом канале с учетом диссипации в безразмерном виде может быть представлено в виде
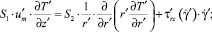(2)
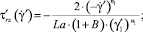
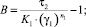
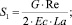
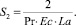
Здесь и далее верхним штрихом обозначены безразмерные величины, полученные с учетом соотношений
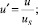
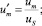
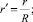
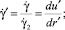
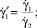
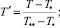
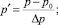
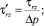
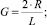
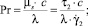
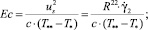
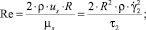
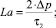
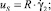
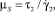
где T = T(r, z) – температура жидкости в канале, представляющая собой неизвестную функцию радиальной r и продольной z координат; u = u(r) – распределение скорости в канале; um – средняя по сечению скорость; S1, S2 – параметры уравнения, определяемые через основные критерии подобия; p, τrz – давление и касательное напряжение соответственно; p0 – давление жидкости на выходе из канала; T**, T*, us, μs – некоторые характерные значения температуры среды в канале, а также скорости жидкости и динамической вязкости, принимаемые в качестве масштабных; B – параметр реологической модели; ρ, c, λ – принимаемые постоянными плотность, теплоемкость, теплопроводность среды соответственно; G, Pr, Ec, Re, La – геометрический критерий подобия, а также критерии подобия Прандтля, Эккерта, Рейнольдса и Лагранжа соответственно.
В уравнении (1) полагали, что учет конвективной составляющей теплопереноса допустимо проводить на основе средней по сечению канала скорости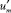 
течения среды в канале, которая определяется следующим образом [2]
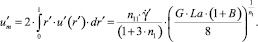
Запишем граничные условия задачи
r′ = 0;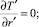 
r′ = 1; 
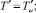z′ = 0;
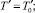
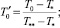
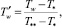(3)
где T0 – температура жидкости на входе в канал; Tw – принимаемая постоянной температура стенки канала.
Решая уравнение (1) с учетом (3), можно показать, что распределение температуры в канале определяется следующим образом
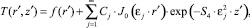(4)
где J0 – функция Бесселя первого рода нулевого порядка; εj – корни характеристического уравнения J0(ε) = 0; Cj – коэффициенты разложения.
В (4) для краткости записи приняты следующие обозначения
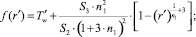(5)
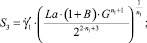
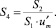
Коэффициенты разложения Cj в (4) с учетом свойства ортогональности базисных функций определяются из выражений
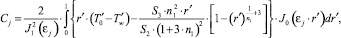j = 1, 2, ...,; и(6)
где J1 – функция Бесселя первого рода первого порядка.
Для оценки влияния основных параметров модели на характеристики диссипативного разогрева жидкости при ее течении в цилиндрическом канале были проведены численные эксперименты на ЭВМ. В качестве примера на рис. 1 представлено распределение безразмерной температуры по радиальной координате в различных поперечных сечениях канала для следующего набора основных параметров системы: G = 0,01; Pr = 1,295∙106; Ec = 2,606∙10–6; Eu = 151,171; Re = 2,646; La1 = 605,04;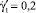 
; B = 0,322; 
; 
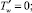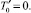Из представленных на этом рисунке данных видно, что распределение температуры не является монотонным. При этом в окрестности стенки канала температурный профиль имеет экстремум типа максимума.
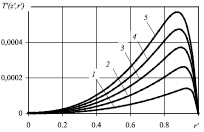
Рис. 1. Распределение безразмерной температуры по радиальной координате при La = 400 для z′ = 0,2 (1); 0,4 (2); 0,6 (3); 0,8 (4); 1,0 (5)
Влияние критерия подобия Лагранжа на распределение температуры в выходном сечении канала при том же наборе прочих исходных параметров системы представлено на рис. 2. Как и следовало ожидать, увеличение критерия подобия Лагранжа приводит для выходного сечения канала к возрастанию как температуры вообще, так и ее пикового значения в частности.
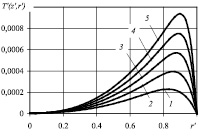
Рис. 2. Распределение безразмерной температуры в выходном сечении канала (z′ = 1) при следующих значениях критерия подобия Лагранжа: La = 200 (1); 300 (2); 400 (3); 500 (4); 600 (5)
Полученные результаты могут быть использованы при моделировании течения неньютоновских жидкостей с соответствующими реологическими свойствами в проточных элементах технологического оборудования.
Работа выполнена при поддержке РФФИ, проект № 12-08-00629.
Рецензенты:
Шашкин А.И., д.ф.-м.н., профессор, заведующий кафедрой «Математический и прикладной анализ», ГОУ ФБГОУ ВПО «Воронежский государственный университет», г. Воронеж;
Буховец А.Г., д.т.н., профессор кафедры «Прикладная математика и применение математических методов в экономике», ГОУ ФБГОУ ВПО «Воронежский государственный аграрный университет им. императора Петра I», г. Воронеж.
Работа поступила в редакцию 01.08.2013.
Библиографическая ссылка
Колодежнов В.Н., Капранчиков С.С., Веретенников А.С. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИССИПАТИВНОГО РАЗОГРЕВА В ЦИЛИНДРИЧЕСКОМ КАНАЛЕ ДЛЯ ЖИДКОСТИ, ДЕМОНСТРИРУЮЩЕЙ ПРОЯВЛЕНИЕ ЭФФЕКТА «ОТВЕРДЕВАНИЯ», ПРИ РЕАЛИЗАЦИИ ПЕРВОЙ СХЕМЫ ТЕЧЕНИЯ // Фундаментальные исследования. – 2013. – № 10-1. – С. 21-24;URL: https://fundamental-research.ru/ru/article/view?id=32207 (дата обращения: 19.04.2024).