В модели DES (Detached Eddy Simulation) область развитого турбулентного течения содержит вихревые структуры различных масштабов, свойства которых зависят от предыстории потока [1, 4]. В DES модели это LES (Large Eddy Simulation) область, непосредственно влияющая на течение в окрестности тела, для разрешения которой требуется качественная сетка. Ячейки сетки здесь должны быть наиболее близки к правильным шестигранникам, поскольку величина характерного размера фильтра является максимальным значением размера счетной ячейки, который должен быть достаточен для разрешения наиболее энергонесущих вихрей [13].
Для правильного разрешения необходимых турбулентных пульсаций в этой области должна использоваться устойчивая и наименее диссипативная схема дискретизации конвективных потоков. В настоящее время практика применения DES моделей в большей своей части сводится к расчетам на многоблочных структурированных сетках с применением схем высокого порядка точности вплоть до седьмого [4]. Построение многоблочных сеток в промышленных конструкциях сложной конфигурации крайне неэффективно [11], а использование схем повышенного порядка точности сильно ограничено ввиду неустойчивого итерационного процесса и большой вычислительной нагрузки. C другой стороны, использование неструктурированной сетки приводит к ряду трудностей, одна из которых заключается в том, что на неструктурированной сетке заметно сужается круг доступных схем для дискретизации конвективных потоков.
Исследование применимости основных схем дискретизации конвективных потоков для DES на неструктурированных сетках можно найти в работах [13, 15]. В работе [15] проводится исследование диссипативных свойств центрально-разностных и противопоточных схем второго порядка на шестигранных и тетраэдральных сетках. На основе анализа полученных результатов делается вывод, что на сетках такого типа нужно использовать схему, основанную на центрально-разностной с использованием искусственной вязкости. Показано, что данная схема приводит к достаточно хорошим результатам при использовании гексагональных сеток. В работе [13] описывается центрально-разностная схема с автоматическим смешением с противопоточной схемой. Фактор смешения строится таким образом, что центрально-разностная схема включается в тех областях, где она наиболее устойчива и необходима для точного разрешения крупномасштабных вихревых структур. В пристеночной области, а также в области, свободной от отрывных вихрей, используется противопоточная схема первого порядка.
Для моделирования турбулентных течений с помощью DES представляется перспективным использование схем семейства NVD. В работе [14] описываются основные представители схем класса NVD (Normalized Variable Diagram), которые ограничиваются с использованием критерия локальной ограниченности (CBC) [7]. В [9] дано обобщение схем NVD на случай использования неструктурированных сеток. Согласно [9] ограничение по критерию CBC гарантирует монотонность схемы, однако вносит дополнительную диффузию. К сожалению, работ по оценке величины вносимой диффузии и исследований применимости данного класса схем для расчета турбулентных течений методом DES найти не удалось, хотя это наиболее важный критерий для применимости схем для DES моделирования. Отметим здесь, что в большинстве работ практически не уделяется внимания используемым численным схемам и их применимости для использования совместно с моделью DES. Кроме того, для используемых численных методов не приводится значения констант модели DES для применяемых схем, тогда как численная реализация и вид схемы, используемой для аппроксимации уравнений, оказывает существенное влияние на значения констант модели DES [15], которые могут отличаться в несколько раз.
В настоящей работе проводится исследование применимости существующих схем аппроксимации конвективных потоков для DES моделирования, которые могут быть реализованы на неструктурированных сетках, состоящих из многогранников произвольной формы [6, 8]. В данной работе в RANS (Reynolds Averaged Navier Stocks) области DES, используются модели имеющие «наивысший рейтинг» применимости при решении прикладных задач: k-e, SST, SA [1]. Калибровка и оценка диссипативности каждой из схем, представленных в работе, осуществляется на решении задачи о вырождении однородной изотропной турбулентности и на задаче развитого турбулентного течения в канале.
Моделирование турбулентности с использованием DES моделей
В рамках подхода DES в RANS и LES областях используется одна базовая модель турбулентности, которая функционирует как RANS модель внутри пристеночного пограничного слоя и как ее подсеточная версия вдали от твердых стенок. Модель турбулентности RANS, на основе которой строится модель DES, может быть преобразована в подсеточную модель для LES путем замены линейного масштаба турбулентности lrans на гибридный линейный масштаб [4]:
ldes = min (lrans, Cdes∆), (1)
где Cdes – дополнительная константа модели, аналогичная константе Смагоринского; Δ – максимальный размер ячейки по всем направлениям. В зависимости от соотношения линейных масштабов RANS и LES модель DES функционирует либо как базовая RANS модель, либо как ее подсеточная версия. В результате в областях потока, в которых используемая сетка является слишком грубой и непригодна для численного разрешения турбулентных структур, DES функционирует как RANS, а в областях с достаточно мелкой сеткой – как подсеточная модель LES.
В данной работе в качестве базовой RANS модели используются три модели: SST Ментера, SA, k–e [1]. В формулировке каждой из них можно выделить линейный масштаб турбулентности:
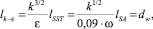 (2)
(2)
где dw – расстояние до твердой поверхности.
В формулировку DES-k-e и DES-SA входит по одной эмпирической константе: Cdes = C k–ε, Cdes = CSA. Модель SST представляет собой комбинацию k – ε и k – ω моделей, поэтому в DES-SST входят уже не одна, а две эмпирические константы CSST_kω и CSST_kε:
Сdes = F1CSST_kω + (1 – F1)CSST_kε, (3)
где F1 – функция из формулировки модели SST.
При DES моделировании в тех областях, где работает подсеточная модель LES, диссипативные свойства схемы, используемой для дискретизации конвективного слагаемого, напрямую влияют на оптимальное значение констант, поэтому для каждого отдельного численного метода константы C k–ε, CSA, CSST_kω, CSST_kε нуждаются в калибровке.
Схемы дискретизации конвективного потока
Выбор оптимальной схемы дискретизации для конвективных потоков – одна из основных проблем при моделировании течений с помощью моделей DES. Схема должна с одной стороны иметь малую диссипацию, т.е. порождать как можно меньше численной диффузии, с другой стороны, она должна обеспечивать стабильный счет на произвольной неструктурированной сетке. Требование малой численной диффузии проистекает из того факта, что при DES моделировании в основной области, где присутствуют вихревые структуры, используется модель LES, и для правильно описания эволюции данных структур необходимо, чтобы численная диффузия схемы была меньше, чем диффузия, которая обеспечивается подсеточной вязкостью модели LES.
Среди большого количества схем дискретизации, можно выделить несколько наиболее часто используемых схем. В данной работе проводится анализ применимости для DES моделирования следующих схем:
- противопоточная схема с линейной интерполяцией (LUD);
- схема QUICK;
- центрально-разностная схема (CD);
- центрально-разностная схема с линейной реконструкцией (CDW);
- схемы семейства NVD;
- гибридные схемы (вышеперечисленные схемы, смешанные с противопоточной схемой для увеличения монотонности).
Схема LUD – противопоточная схема с использованием реконструкции величины на грань с линейной интерполяцией [1, 8]. Схемы CD и CDW – наименее диссипативные схемы, однако они неустойчивы [1, 10], и при наличии больших градиентов их использование приводит к осцилляциям в поле решения. Схема QUICK [10] является схемой смешанного типа, она сочетает в себе противопоточную схему первого порядка совместно с градиентной поправкой и схему CD. Такой подход позволяет убирать диссипативные ошибки первого порядка и подавлять осцилляции второго порядка. Схемы семейства NVD основаны на использовании диаграмм нормализованной переменной и критерия ограниченности CBC [7]. В своей изначальной форме построение функции нормализованной переменной основано на использовании структурированной сетки. Наиболее удобным обобщением схем NVD на произвольные неструктурированные сетки рассмотрено в работе [9], там же предложена сама схема семейства NVD – схема GAMMA. Схема GAMMA имеет в основе своей схему CD, но использует функцию нормализованной переменной для применения критерия ограниченности CBC. Схема GAMMA более диссипативна, чем CD, однако приводит к ограниченному решению искомой величины. Также схема имеет один свободный параметр, который определяет вклад противопоточной составляющей в результурующее значение величины на грани и в конечном счете влияет на быстроту сходимости.
Гибридные схемы представляют собой линейную комбинацию схемы высокого и низкого порядков [8], что приводит к увеличению монотонности решения. Гибридную схему, например, для схемы CD и противопоточной схемы UD, можно записать следующим образом:
φF,gibr = γφF,CD + (1 – γ)φF,ud, (4)
где γ – коэффициент смешения. В настоящей работе рассматриваются гибридная схема на основе CD и UD, и схема на основе CDW и LUD, с постоянным коэффициентом смешения γ = 0,9.
Оценка диссипативности схем и калибровка констант DES модели
Оценка диссипативности схем проводится путем решения задачи о вырождении однородной изотропной турбулентности [5]. Однородная изотропная турбулентность – достаточно редко реализующееся в природе явление, но его моделирование помогает с хорошей точностью узнать насколько диссипативна та или иная схема дискретизации конвективных потоков. По диссипативности можно оценить пригодность каждой схемы для DES расчетов в области, где функционирует подсеточная модель LES.
Для всех расчетов настоящей работы используется пакет программ ЛОГОС – российский продукт инженерного анализа, предназначенный для решения сопряженных трехмерных задач конвективного тепломассопереноса, аэродинамики и гидродинамики на параллельных ЭВМ [2, 3]. Для численного решения задач течения вязкой несжимаемой жидкости, представленных в данной работе, используется метод SIMPLE, основанный на процедуре расщепления полной системы уравнений Навье‒Стокса с итерационной процедурой коррекции давления [1, 8].
Моделирование задачи проводится в расчетной области размером 2π×2π×2π с количеством ячеек 64×64×64 по всем трем направления соответственно. По всем трем пространственным координатам используется периодическое граничное условие. По заданному начальному энергетическому спектру формируется случайное поле скоростей, которое используется в качестве начального условия. Далее производится нестационарный расчет задачи до момента времени 0,87 секунд, после чего результаты сохраняются и переводятся обратно в энергетический спектр, который сравнивается с экспериментальными данными [5]. По поведению кривой энергетического спектра можно судить о качестве каждой схемы – занижение энергии в том или ином интервале говорит о ее диссипативности.
Для сравнения схем по уровню численной диссипации наиболее удобно использовать модель с одной константной, чтобы избежать большого количества вариантов расчетов. В данной работе для сравнения схем по уровню диссипативности использовалась модель турбулентности DES-SA с двумя значениями константы: рекомендованное значение для центрально разностных схем CSA = 0,62 [15] и значение на порядок меньшее CSA = 0,062, которое взято для того, чтобы оценить позволит ли резкое уменьшение подсеточной вязкости добиться правильного описания энергетического спектра для схем, имеющих большую численную диссипацию.
Для дискретизации по времени используется схема Кранка‒Николсона, шаг по времени соответствует числу Куранта CFL = 1 . На каждом шаге по времени проводится 10 внутренних итераций решателя, что обеспечивает сходимость невязок основных физических величин до δ = 1 ∙10–8 по норме L1.
На рис. 1 представлены результаты расчета задачи для схем LUD, QUICK, GAMMA для CSA = 0,62 и CSA = 0,062. Данные схемы достаточно диссипативны, и в области высоких частот при любых значениях константы наблюдается занижение энергии пульсаций. Даже снижение на порядок значения CSA, а, следовательно, и подсеточной вязкости, не приводит к правильной картине. Это означает, что даже на шестигранной сетке в области эволюции вихревых структур данные схемы будут неправильно описывать процесс каскадной передачи энергии от крупных вихрей к мелким и для DES моделирования они, вообще говоря, не пригодны.
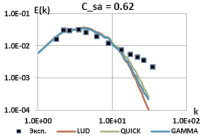
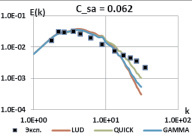
Рис. 1. Энергетические спектры, схемы LUD, QUICK, SOU, GAMMA
На рис. 2 представлены результаты для схем CD, CDW, а также для двух гибридных схем: на основе CD и UD с γ = 0,9 (обозначим 0,9CD + 0,1UD) и на основе CDW и LUD с γ = 0,9 (обозначим 0,9CDW + 0,1LUD). Данные схемы удовлетворяют требованию по уровню численной диссипации, поскольку при CSA = 0,062 у всех схем наблюдается завышение энергетического спектра в области низких частот. Это означает, что путем увеличения константы CSA, а, следовательно, и уровня подсеточной вязкости, можно добиться правильного описания процесса затухания изотропной турбулентности.
Таким образом, среди рассмотренных схем дискретизации для DES моделирования в области LES пригодны лишь четыре из них: CD, CDW, 0,9CD + 0,1UD, 0,9CDW + 0,1LUD. Данные схемы имеют приемлемый уровень диссипации и для них можно определить уровень подсеточной вязкости, который обеспечит правильное описание эволюции вихревых структур.
Для выбранных схем проведем калибровку констант всех рассматриваемых моделей DES. Калибровка констант DES моделей проводится путем решения той же задачи о вырождении однородной изотропной турбулентности с варьированием значений констант. На рис. 3 показаны результаты расчета с константами, значение которых обеспечило наилучшее совпадение результирующего спектра с экспериментальным [5].
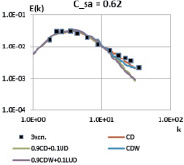
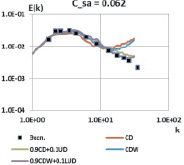
Рис. 2. Энергетические спектры, схемы CD, CDW, гибридные
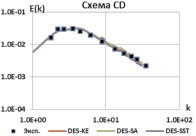
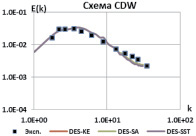
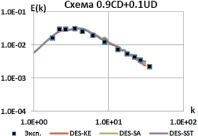
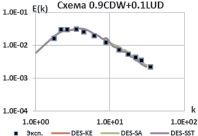
Рис. 3. Энергетические спектры, калибровка моделей DES
Результирующие оптимальные значения констант для каждой модели DES и для каждой рассматриваемой схемы приведены в таблице.
Оптимальные значения эмпирических констант
|
CD |
CDW |
0,9CD + 0,1UD |
0,9CDW + 0,1LUD |
|
|
Ck–ε |
1,20 |
1,18 |
0,61 |
0,60 |
|
CSA |
0,62 |
0,60 |
0,33 |
0,31 |
|
CSST_kω |
0,78 |
0,72 |
0,39 |
0,38 |
|
CSST_kε |
0,61 |
0,58 |
0,31 |
0,30 |
Далее, на примере расчета турбулентного течения в плоском канале, будет показано, что использование полученных наборов констант для каждой схемы обеспечивает правильное описание эволюции вихревых структур в области, где при DES моделировании работает подсеточная модель LES.
Расчет развитого турбулентного течения в канале
В задаче рассматривается развитое течение несжимаемой жидкости в плоском канале с высотой 1 м при числе Рейнольдса, построенном по высоте канала и динамической скорости, равном Reτ = 800, что соответствует условиям, при которых в работе [12] выполнен DNS расчет данного течения.
Расчетная сетка содержит сгущения к областям твердых поверхностей. Общее количество ячеек составляет 1,2 млн. На твердых стенках компоненты скорости, турбулентная вязкость и кинетическая энергия турбулентности полагаются равными нулю. На остальных границах для всех переменных используется условие периодичности. Для того чтобы обеспечить движение, в уравнение переноса продольной составляющей импульса вводится дополнительный член, равный градиенту давления при установившемся течении в канале: Па/м.
Для определения осредненных характеристик течения вначале выполнялся нестационарный расчет до выхода решения на статистически установившийся режим. Далее расчет продолжался с вычислением осредненной горизонтальной скорости и осредненных компонент тензора турбулентных пульсаций.
В качестве модели турбулентности использовались три модели DES (DES-ke, DES-SA, DES-SST) с различными схемами дискретизации конвективных слагаемых в уравнениях переноса импульса и соответствующими наборами констант из таблицы.
На рис. 4–5 представлены профили средней скорости и разрешенных компонент тензора напряжений Рейнольдса для каждой схемы в сравнении с результатами, полученными при DNS расчете [12].
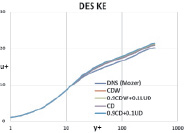
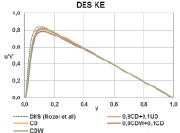
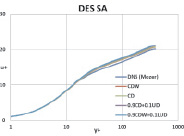
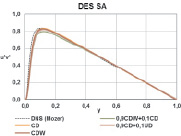
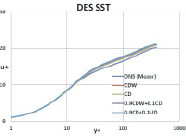
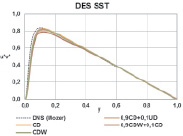
Рис. 4. Профиль скорости и профиль разрешенных напряжений Рейнольдса
По осредненному профилю скорости и профилю разрешенных напряжений Рейнольдса получено хорошее согласие с DNS расчетами. Также наблюдается хорошее согласие результатов, полученных при использовании разных схем дискретизации. Таким образом, по результатам можно сделать вывод, что при использовании разных схем дискретизации с соответствующим набором констант, полученных ранее, описание эволюции вихревых структур производится корректно.
Заключение
В статье исследована применимость различных схем дискретизации конвективного слагаемого уравнений Навье‒Стокса при моделировании турбулентных течений методом отсоединенных вихрей. Для каждой исследуемой схемы определен уровень численной диссипации и сделан вывод о ее эффективности для расчета эволюции вихревых структур в области, где при DES моделировании используется подсеточная модель LES.
Исследование показало, что среди рассмотренных схем приемлемый уровень численной диссипации могут обеспечить только четыре схемы: CD, CDW, гибридные 0,9CD + 0,1UD и 0,9CDW + 0,1LUD. Для них были откалиброваны эмпирические константы трех моделей DES: DES-k-e, DES-SA, DES-SST.
В результате численных расчетов было получено в общем числе 12 наборов эмпирических констант для соответствующих моделей и схем, использование которых обеспечивает правильное описание эволюции вихревых структур при DES моделировании. На примере задачи о развитом турбулентном течении в канале показано, что использование полученных наборов констант с разными схемами дискретизации дает похожие результаты, которые хорошо согласуются с результатами DNS расчетов.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (государственный контракт № 14.514.12.0002) и частично при поддержке Российского фонда фундаментальных исследований в рамках научного проекта № 13-07-12079.
Рецензенты:
Дерюгин Ю.Н., д.ф.-м.н., начальник отдела, ФГУП РФЯЦ ВНИИЭФ, г. Саров;
Куркин А.А., д.ф.-м.н., профессор, заведующий кафедрой «Прикладная математика» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород.
Работа поступила в редакцию 18.09.2013.Библиографическая ссылка
Козелков А.С., Курулин В.В., Тятюшкина Е.С., Пучкова О.Л., Лашкин С.В. ИССЛЕДОВАНИЕ СХЕМ ДИСКРЕТИЗАЦИИ КОНВЕКТИВНОГО ПОТОКА ДЛЯ МОДЕЛИРОВАНИЯ ТУРБУЛЕНТНЫХ ТЕЧЕНИЙ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ МЕТОДОМ ОТСОЕДИНЕННЫХ ВИХРЕЙ // Фундаментальные исследования. – 2013. – № 10-5. – С. 1051-1058;URL: https://fundamental-research.ru/ru/article/view?id=32451 (дата обращения: 26.04.2024).



