Управление сложными техническими системами определяет необходимость разработки соответствующих алгоритмов. В качестве примера таких систем, активно используемых на практике, могут быть приведены мехатронно-модульные роботы (ММР). В настоящее время многие предприятия, которые создают роботов, применяют системы автоматизированного проектирования (САПР) для того, чтобы формировать роботов на основе виртуальной среды. В основе указанных САПР находятся специальные приложения, предназначенные для того, чтобы моделировать геометрические, кинематические и эргономические характеристики робота [2]. При этом могут формироваться различные варианты робототехнического устройства проектировщиком на основе применения средств геометрического моделирования.
Методика решения задачи
При формировании структуры робота может применяться комбинированный поисковый алгоритм, который состоит в использовании процедуры многоальтернативной оптимизации для получения некоторого набора хороших вариантов, которые достаточно полно отвечают требованиям оптимизируемой функции F [1, 7]. При выборе конечного варианта подключается алгоритм поиска, характеризующийся более высокой эффективностью для рассматриваемого класса объектов проектирования. В [3, 5] на основе модельных экспериментов показана возможность применения генетических алгоритмов для структурного синтеза ММР.
Используется определенная структура хромосомы, кодирующей порядок сборки и алгоритм управления ММР.
В случае алгоритма многоальтернативного выбора будем рассматривать значения альтернативных переменных xj,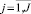 
, принимающих значения 1 или 0 как коды соответствующих генов хромосомы.
В отличие от формата хромосомы, предложенном в [6], формат хромосомы, являющийся аналогом перспективного варианта решения задачи многоальтернативной оптимизации, в соответствии с оптимизируемой функцией F включает ряд блоков хромосом в следующей последовательности:
1) подхромосома, состоящая из четырех генов и определяющая количество N модулей ММР;
2) N – 1-подхромосома, состоящая из пяти генов и определяющая размещение модуля (2 гена – сторона крепления, 3 гена – номер площадки, выбранной для стыковки);
3) N-подхромосомы, состоящие из четырех генов и определяющие параметры управления первой степенью подвижности модуля (по обобщенной координате y);
4) N-подхромосомы, состоящие из четырех генов и определяющие параметры управления второй степени подвижности модуля (по обобщенной координате z).
На первом этапе осуществляется переформатирование блоков 2–4 в формат, когда последовательно для каждого модуля располагаются гены xj,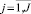 
, характеризующие размещение модуля и алгоритм управления. Обозначим хромосомы в этом формате xℓ = (xjℓ), 
, 
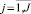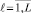, где ℓ – число перспективных доминирующих вариантов (L обычно ≤ 7 [3]).
На втором этапе используются основные операции генетических алгоритмов, апробированные для ММР [6]: скрещивания и размножения. Учебно-исследовательская составляющая предусматривает выбор из нескольких схем скрещивания.
Для выполнения скрещивания все хромосомы xℓ,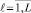 
, принадлежащие популяции X, делят на локальные популяции Xm ≠ 0, 
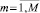(M ≤ J), в любой из которых равны нулю Хемминговы расстояния между любой парой генов xjℓ, xjt, 
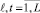. Локальные популяции для скрещивания выбираются случайным образом. Для этого определяется численность локальных популяций Lm и для случайного выбора используется распределение вероятностей
pm = Lm/L,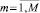 
. (1)
Определяются реализации случайного дискретного числа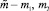 
. В качестве родительской пары (xℓ, xt) ∈ X выбираются хромосомы xℓ ∈ Xm1 и xt ∈ Xm2.
Вторая схема скрещивания определяется расстоянием Хемминга между значениями xjℓ, xjt,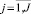 
двух хромосом xℓ, xt, 
, 
.
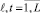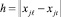В случаях h ≤ h0, где h0 – заданное положительное число, исследуется схема имбридинга. Если h ≥ h0, исследуется третья схема – аутбридинга.
Кроме приведенных схем исследуются схемы ассортативного скрещивания. В этом случае используется количественная оценка степени приспособления, которая определяется по значению оптимизируемой функции для каждой хромосомы xℓ – F(xjℓ). В первой схеме хромосомы для скрещивания выбираются из распределения вероятностей
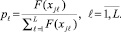(2)
Во второй схеме при проведении отрицательного ассортативного скрещивания делают случайный выбор одной из хромосом из (2), а вторая берется из вероятностей
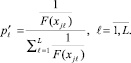(3)
Третья схема основана на селективном скрещивании. С этой целью из набора хромосом xℓ,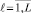 
исключаются те, которые обладают степенью приспособленности меньшей, чем средняя степень приспособленности на множестве хромосом xℓ, 
:
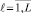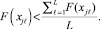
Далее осуществляется случайный выбор по распределению (2).
Особенности реализации генетического алгоритм
Для операции размножения используется рекомбинация генов двух родительских хромосом, выбранных на основе скрещивания. При этом получаем новый вариант набора альтернативных переменных, определяющих конструкцию и алгоритм управления движением. Родительские хромосомы сравниваются по содержанию каждого гена. В учебно-исследовательской составляющей УИ САПР целесообразно рассмотреть возможные реализации операции размножения. Далее переходят к одной из схем скрещивания для подбора вариантов xℓ, xt,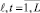 
, в родительскую пару. При этом происходит завершение процесса после осуществления перебора всех возможных родительских пар. С целью проведения сокращений множества перспективных вариантов создается репродукционная группа с использованием селекционных схем. Здесь исследуются две основные схемы. В первой схеме происходит упорядочение всех 
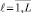в том порядке, в котором идет убывание для значений, характеризующих их степени приспособленности. Задают размер для репродукционной группы Lp, с ограничением перспективных вариантов. Для второго случая определяют среднюю степень приспособленности 
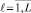вариантов
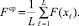
В репродукционную группу происходит включение только тех вариантов xlp, у которых степень приспособленности выше или равна средней величине
F(xℓ) ≥ Fср,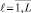 
.
Поскольку алгоритм многоальтернативной оптимизации [1, 7] основан на организации поиска для рандомизированной среды, следует размещать в этой среде и процедуру, которая дает выбор свертки. При этом в рандомизированной среде используют случайную величину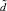 
, которая принимает значение номеров, относящихся к функциям 
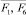c вероятностью Pd, 
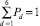. На k-м шаге одновременно c проведением настройки вероятностей, характеризующих альтернативные переменные, вероятностей, характеризующих значимости критериев ψi(x) при формировании оптимизируемых функций, идет настройка вероятностей Pd на основе такой последовательности шагов.
1. Исходя из распределения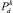 
происходит генерация значений дискретного случайного числа 
.
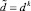2. В том случае, когда dk = 1, то исходя из распределения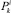 
происходит генерация дискретного случайного числа 
.
3. Происходит определение четырех значений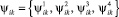 
для различных комбинаций по альтернативным переменным хj, 
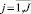, которые соответствуют первой Δ1jψik и второй Δ2jψik вариациям в алгоритме многоальтернативной оптимизации.
4. В том случае, когда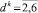 
, то, исходя из вариаций Δ1jFdkΔ2jFdk алгоритма многоальтернативной оптимизации, происходит вычисление четырех значений оптимизируемой функции
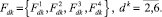
5. Происходит вычисление для таких же комбинаций по альтернативным переменным на основе четырех значений для других критериев ψi, i ≠ ik.
6. Среди всех критериев ψi и функций Fdk,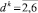 
из четырех значений происходит выбор рекорда (максимального значения 
, 
, 
).
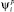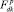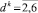7. Полученные рекордные значения предъявляют для эксперта с целью оценивания с вопросом: «Какое из предъявленных значений по критериям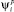 
и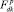 
не приводит к удовлетворению условий в максимальной степени?».
8. В том случае, если подходит один из данных критериев ψi то происходит настройка по вероятностям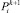 
и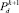 
, когда не устраивает 
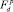, то проводится настройка только для 
.
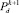9. Происходит формализация ответа эксперта таким образом
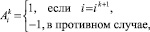
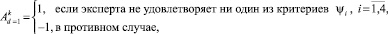
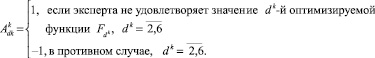
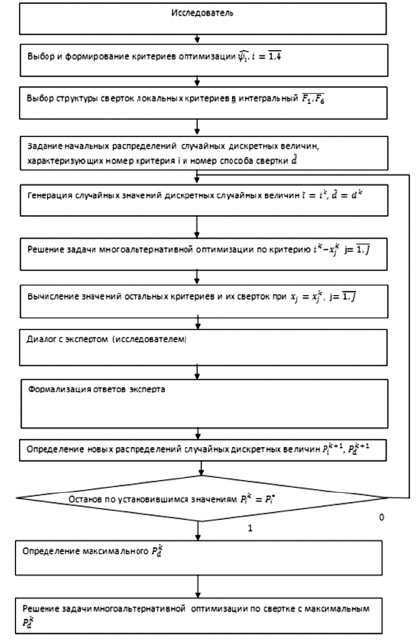
Структурная схема диалогового алгоритма многокритериальной оптимизации на множестве альтернативных переменных
10. Происходит определение нового распределения для случайных дискретных величин 
, 
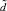исходя из информации, которая получена из диалога с экспертом и для которой есть формализация по правилам п. 9, и с ориентацией на условия п. 8,
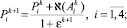
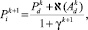
где εk+1 > 0 – размер шага при получении значений вероятностей Pi на k + 1-й итерации; γk+1 > 0 – размер шага при получении значений вероятностей Pd на k + 1-й итерации,
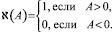
11. Отмечаются установившиеся значения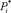 
исходя из того, как зависит Pi от номера итерации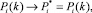 
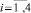
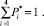
12. С итерации k = K происходит переход от проведения поиска по выбранным критериям ψi,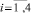 
к проведению поиска на основе аддитивной свертки, ориентируясь на следующее условие:
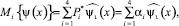
считая, что
,
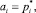
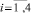где Mi – математическое ожидание реализаций значения ψi(x) по случайному дискретному числу 
.
13. Происходит сравнение значений, определенных в п. 10 для k-й итерации. По следующему шагу в алгоритме многоальтернативной оптимизации происходит выбор оптимизируемой функции Fd с наибольшим значением pd.
Структурная схема диалогового алгоритма многокритериальной оптимизации приведена на рисунке.
Выводы
Таким образом, в работе проведена интеграция алгоритма многоальтернативного выбора и генетического алгоритма. Разработанный алгоритм позволяет исследовать особенности движения ММР. Приведена структурная схема диалогового алгоритма многокритериальной оптимизации на множестве альтернативных переменных.
Рецензенты:
Разинкин К.А., д.т.н., профессор Воронежского государственного технического университета, г. Воронеж.
Чопоров О.Н., д.т.н., профессор, проректор по научной работе Воронежского института высоких технологий, г. Воронеж.
Работа поступила в редакцию 06.11.2013.
Библиографическая ссылка
Андраханов С.В., Львович Я.Е., Преображенский А.П. РЕАЛИЗАЦИЯ ИНТЕГРИРОВАННОГО АЛГОРИТМА МНОГОАЛЬТЕРНАТИВНОГО ВЫБОРА И ГЕНЕТИЧЕСКОГО АЛГОРИТМА // Фундаментальные исследования. – 2013. – № 10-11. – С. 2391-2395;URL: https://fundamental-research.ru/ru/article/view?id=32801 (дата обращения: 20.04.2024).