Главной особенностью современного мира, играющей важную роль для школы, стал значительный рост объёма информации, обязательной для изучения школьниками в рамках различных учебных предметов. Эта проблема становится ещё более актуальной в связи с уменьшением количества часов по всем предметам, подготовкой к ЕГЭ в 10–11 классах и новыми требованиями Федерального Государственного стандарта.
Перспективным выходом из сложившейся ситуации видится фреймовый подход к процессу обучения, сущность которого заключается в свёртывании укрупнённых дидактических единиц учебного материала и языковом или знаковом их представлении, что обеспечивает компактное представление, свёртывание и сжатие информации. Ключевым понятием фреймового подхода является фрейм, который определяется Э.Г. Гельфман и М.А. Холодной [2], как форма хранения стереотипных знаний о некотором классе ситуаций: его «каркас» характеризуют устойчивые, всегда имеющие место отношения между элементами объекта или ситуации, а узлы этого каркаса – вариативные детали данной ситуации или объекта. В Кратком словаре когнитивных терминов [7] фрейм характеризуется как бланк, имеющий пустые строки, графы, окна – слоты, которые должны быть заполнены. Фрейм как компактное представление знаний появляется вследствие аналитико-синтетической обработки учебной информации и представляет собой её абстрактный образ, который актуализируется в типовых ситуациях и служит для их понимания и объяснения. Р.В. Гурина и Е.Е. Соколова [3] выделяют следующие признаки фреймов для представления знаний: стереотипность, повторяемость, наличие ограничения, возможность визуализации, ключевые слова, ориентированность на восприятие конкретным учащимся, универсальность, наличие каркаса с пустыми окнами, ассоциативные связи, фиксация аналогий, обобщений, правил и принципов.
Реализация фреймового подхода к процессу обучения математике возможна при осуществлении индивидуальной проектно-исследовательской деятельности, развитие которой может быть организовано в рамках различных учебных предметов, но, по нашему мнению, в большей степени на математике.
Это связано с тем, что, во-первых, математика в 10–11 классах является завершающим и систематизирующим разделом школьной математики, в котором даются фундаментальные основы построения математических знаний и указывается связь с предметами естественнонаучного цикла. Во-вторых, изучение математики 10–11 классов позволяет учащимся приобрести опыт осуществления мысленного эксперимента как одного из способов овладения математическим инструментарием – математическими моделями. В-третьих, гуманитарный и прикладной характер математики 10–11 классов позволяет развивать навыки математического исследования, развивать научную интуицию и рефлексию учащихся. Совокупность содержательного и процессуального компонентов математики 10–11 классов позволяет организовать на её основе индивидуальную проектно-исследовательскую деятельность учащихся.
В исследовании под индивидуальной проектно-исследовательской деятельностью понимается процесс достижения цели, который выстраивается по индивидуальной образовательной траектории на основе самостоятельного поиска теоретических знаний, предвидения и прогнозирования способов и процессов деятельности, и завершается реальным практическим или теоретическим результатом. Основываясь на результатах Н.В. Матяш [8], в исследовании представлены этапы индивидуальной проектно-исследовательской деятельности: ситуационно-исследовательский (формулировка и обоснование цели, анализ предстоящей деятельности, выбор средств и инструментов, разработка плана деятельности), инструментально-операциональный (выполнение соответствующих операций, самоконтроль деятельности), рефлексивно-оценочный (самооценка, сравнение результатов и замысла, анализ полученных знаний, подведение итогов и формулирование выводов).
Поэтапное осуществление индивидуальной проектно-исследовательской деятельности способствует самостоятельному приобретению информации в удобном для учащихся темпе и на необходимом уровне. Организованная таким образом работа с математической информацией позволяет рассматривать процесс обучения с позиций ситуационного подхода, который развивает одно из ключевых положений системного подхода, предполагая, что эффективность в решении проблемы зависит от данного сочетания условий, фактов и обстоятельств. Ситуация, как механизм воздействия, включает рефлексию, осмысление, переосмысление сложившихся обстоятельств, ставя перед учащимися новые условия, требующие нестандартных подходов и решений. С позиций ситуационного подхода учебная математическая задача выступает как задача-ситуация, под которой в исследовании понимается данная в определенных условиях и обстоятельствах цель деятельности, которая достигается определенной последовательностью действий, соответствующих сложившейся ситуации. Последовательность действий предполагает: осознание ситуации, построение схемы (образа) ситуации, её теоретическое обоснование и практическое применение. В процессе решения задач-ситуаций возникают различные математические ситуации, деятельность по разрешению которых предполагает использование эксперимента.
Т.Н. Шамало, определяя роль и место эксперимента в процессе обучения физике, делает акцент на его полифукциональность, обращая внимание, что роль эксперимента заключается не только в создания понятийного аппарата определённой предметной области, но и в развитии мышления в целом [11].
В.И. Арнольд утверждает, что математика является экспериментальной наукой и отличается от физики тем, что в математике эксперименты очень дешевы. По словам автора, неотъемлемая часть математического образования должна содержать умения составлять адекватные математические модели реальных ситуаций и математический подход к явлениям реального мира [1].
В.И. Загвязинский подчеркивает, что одним из точных методов изучения явлений, фиксирования фактов, слежения за изменением и развитием объекта исследования является эксперимент [5].
В работах В.В. Давыдова применяется понятие «мыслительного эксперимента», который, по словам автора, направляет учащихся на приобретение знаний как результата преобразования учебного материала, позволяющего вскрыть в нём существенные отношения и проследить происхождение внешних его проявлений [4].
По мнению авторов [3, 6], эксперимент представляет собой целенаправленное действие исследователя на объект для изучения его различных сторон, связей и отношений и включает в себя три взаимосвязанных этапа: подготовительный, сбор экспериментальных данных и обработку результата.
Поэтапное выполнение эксперимента для решения задачи-ситуации предполагает обращение учащегося к опыту осуществления индивидуальной проектно-исследовательской деятельности. На подготовительном этапе эксперимента происходит осознание соответствующей ситуации, принятие цели деятельности, задание условий и выбор средств эксперимента, что соответствует ситуационно-исследовательскому этапу индивидуальной проектно-исследовательской деятельности. Второй этап эксперимента направлен на работу с объектом изучения, выполнение соответствующих технологических операций, многократную повторность измерений и строгий учёт факторов, влияющих на исследуемый объект, указанные действия включены в инструментально-операциональный этап. Анализ и интерпретация результатов эксперимента, построение схемы или образа изучаемого объекта, установление причинно-следственных связей между заданными условиями и характеристиками исследуемого объекта позволяют сделать вывод о близости третьего этапа выполнения эксперимента с рефлексивно-оценочным этапом индивидуальной проектно-исследовательской деятельности.
Раскрытие этапов проведения эксперимента и осуществления индивидуальной проектно-исследовательской деятельности в процессе обучения математике в 10–11 классах позволило выявить их связь и обосновать целесообразность использования эксперимента в развитии индивидуальной проектно-исследовательской деятельности. В ходе осуществления эксперимента основным является приём варьирования действий с одним и тем же математическим объектом, который, по мнению Э.К. Гельфман и М.А. Холодной [2], может быть использован для получения фрейма, как структуры данных, представляющей собой собственный опыт учащихся, обобщенный в аналитическую схему, в которой присутствуют узлы информации, связи и отношения. Для получения фрейма в процессе осуществления эксперимента необходимо использовать вопросы и задания, позволяющие выделить инвариантные и вариативные характеристики математических объектов или ситуаций. В процессе выполнения предложенных заданий учащиеся, получая новую для себя ситуацию, выбирают из своей памяти некоторую структуру данных, чтобы путем изменения в ней некоторых деталей сделать ее пригодной для понимания более широкого класса явлений или процессов.
Приведём примеры фреймов, полученных в процессе выполнения эксперимента, который применяется для решения задач-ситуаций в рамках развития индивидуальной проектно-исследовательской деятельности учащихся в процессе обучения математике в 10–11 классах. Тема: «Общие методы решения уравнений» по учебнику «Математика. 11 класс», авторы А.Г. Мордкович, И.М. Смирнова и др. [10].
Цель: сформировать представление учащихся об общих идеях и методах решения уравнений.
Рассмотрите решенные примеры уравнений, сформулируйте суть каждого из них, соотнесите её с названием метода решения, результат занесите в схему (рис. 2).
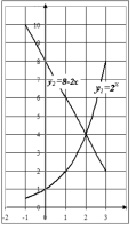
Рис. 1. Графики функции y1 = 2x и y2 = 8 – 2x
Пример 1. 2x = 8 – 2x. Рассмотрим функции y1 = 2x и y2 = 8 – 2x. Построим графики этих функций (рис. 1). Графики функций пересекаются в одной точке (2; 4). Абсцисса этой точки является корнем уравнения.
Ответ: x = 2.
Пример 2.
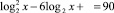
Найдём ОДЗ: x > 0.
Заменим log2x = t. Получим уравнение относительно t: t2 – 6t + 9 = 0, Преобразуем это уравнение, используя формулу квадрата разности: (t – 1)2 = 0, т.е. t – 1 = 0, t = 1. Выполним обратную замену: log2x = 1, 21 = x, x = 2.
Ответ: x = 2.
Пример 3.
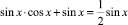
Преобразуем уравнение и разложим на множители
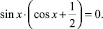
Представим полученное уравнение в виде совокупности двух уравнений и решим её:
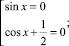
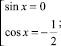
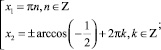
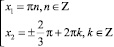 .
.
Ответ:
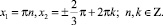
Пример 4. (2x + 2)7 = (5x – 9)7 Так как функция y = z7 монотонная, то перейдём к уравнению 2x + 2 = 5x – 9, откуда находим 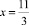 .
.
Ответ: 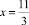 .
.
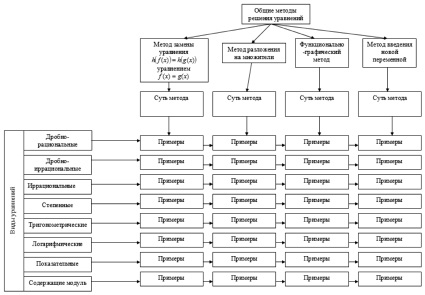
Рис. 2. Пример фрейма-схемы по теме: «Общие методы решения уравнений»
Решите предложенные уравнения, определите вид и метод решения каждого из них, результат занесите в схему (рис. 2):
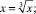
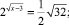
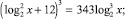
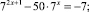
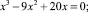
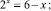
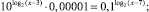
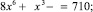
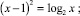
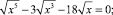
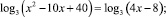
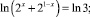
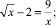
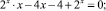
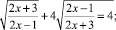
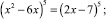
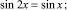
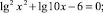
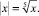
Есть ли среди перечисленных уравнений такие, которые можно отнести к нескольким видам и/или для решения которых используется несколько методов?
Запишите такие уравнения в таблицу и приведите свои примеры (таблица).
Пример фрейма-таблицы, который отражает информацию о нестандартных ситуациях
|
№ п/п |
Пример уравнения |
Вид уравнения |
Методы, используемые в его решении |
|
1. |
|||
|
2. |
Решив эту задачу-ситуацию, учащиеся получат фрейм-схему, в которой представлена сжатая и структурированная информация по теме, и фрейм-таблицу, отражающую информацию о нестандартных ситуациях при решении уравнений.
Информационная ёмкость, структурированность и компактность фреймов, полученных в результате выполнения эксперимента для решения задач-ситуаций, ещё раз подтверждают целесообразность использования фреймового подхода к развитию индивидуальной проектно-исследовательской деятельности в процессе обучения математике в 10–11 классах.
Рецензенты:
Асланов Р.М., д.п.н., профессор кафедры математического анализа, ФГБОУ ВПО «Московский педагогический государственный университет», г. Москва;
Мерлина Н.И., д.п.н., профессор кафедры дискретной математики и информатики Чувашского государственного университета им. И.Н. Ульянова, г. Чебоксары.
Работа поступила в редакцию 06.11.2013.
Библиографическая ссылка
Косиков А.В. ФРЕЙМОВЫЙ ПОДХОД К ОРГАНИЗАЦИИ ИНДИВИДУАЛЬНОЙ ПРОЕКТНО-ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ В ПРОЦЕССЕ ОБУЧЕНИЯ МАТЕМАТИКЕ В 10–11 КЛАССЕ // Фундаментальные исследования. – 2013. – № 10-11. – С. 2519-2523;URL: https://fundamental-research.ru/ru/article/view?id=32827 (дата обращения: 24.04.2024).



