В результате реформирования современного российского высшего образования все вузы выстраиваются в своеобразную иерархическую пирамиду, вершиной которой являются два вуза-лидера (МГУ и СПбГУ), затем следуют федеральные (ФУ) и национальные исследовательские (НИУ) университеты и т.д. [9, 10, 13, 14]. В 2013 году был определен перечень ведущих конкурентоспособных российских вузов (ВКВУЗ) – получателей субсидий для повышения конкурентоспособности на мировой арене [1]. Одним из основных показателей оценки эффективности образовательной деятельности вузов является средний балл ЕГЭ студентов, принятых по результатам ЕГЭ [10, 12, 13]. При этом по совокупности показателей оценки эффективности деятельности вузов формируется сводный показатель. В данной работе, аналогично [2–5, 8], проведен кластерный анализ российского элитного образования на основе вступительных испытаний 2013 г., в значительной степени опирающихся на результаты ЕГЭ как индикатор качества обучения [11]. Рейтинг вузов РФ по среднему баллу ЕГЭ (mЕГЭ) [7], показывающий уровень знаний абитуриентов 2013 года, поступивших на бюджетные места в государственные вузы страны, возглавляет МГИМО, у которого средний балл ЕГЭ – 95,6 по 100-балльной шкале. В табл. 1 для выборки ВКВУЗ, расширенной лидерами МГУ и СПбГУ, из показателей вступительных испытаний (ПВИ) кроме mЕГЭ приведены также разность mЕГЭ между 2013 и 2012 гг. (Dm), количество студентов, зачисленных на бюджетные места (N), а также количество студентов (в % к N), принятых на бюджетные места по конкурсу баллов ЕГЭ (NЕГЭ), по олимпиадам (NО) [6] и по целевому набору (NЦ).
Таблица 1
ПВИ 2013 г. ВКВУЗ
|
Ранг ВКВУЗ (mЕГЭ) |
Ранг вузов (mЕГЭ) |
ВКВУЗ |
mЕГЭ, баллы |
Стандартизированная шкала |
|||||
|
mЕГЭ |
Dm |
NЕГЭ |
NО |
NЦ |
N |
||||
|
1 |
2 |
НИУ МФТИ |
93,2 |
1,8 |
–1,1 |
0,6 |
–0,1 |
–0,5 |
–0,9 |
|
2 |
4 |
НИУ ВШЭ |
89 |
1,3 |
–1,2 |
–3,3 |
3,4 |
–1,1 |
0,3 |
|
3 |
6 |
МГУ |
88,1 |
1,2 |
–0,7 |
0,4 |
0,2 |
–1,0 |
2,3 |
|
4 |
7 |
СПбГУ |
87,8 |
1,2 |
–0,1 |
0,3 |
0,1 |
–1,2 |
0,9 |
|
5 |
16 |
НИУ МИФИ |
84,6 |
0,8 |
2,2 |
0,2 |
–0,5 |
0,8 |
–1,0 |
|
6 |
29 |
Новосиб. гос. НИУ |
82,2 |
0,5 |
0,4 |
–0,1 |
0,8 |
–1,4 |
–0,9 |
|
7 |
47 |
НИУ СПб ИТМО |
80,5 |
0,3 |
–0,1 |
–0,3 |
0,6 |
–0,3 |
–0,5 |
|
8 |
72 |
Казанский ФУ |
76,8 |
–0,1 |
0,4 |
0,8 |
–0,7 |
–0,1 |
0,6 |
|
9 |
78 |
СПб политехн. НИУ |
75,8 |
–0,3 |
–0,0 |
–0,4 |
–0,2 |
1,0 |
0,4 |
|
10 |
90 |
НИУ МИСиС |
74,6 |
–0,4 |
1,4 |
1,4 |
–0,7 |
–0,7 |
–1,2 |
|
11 |
94 |
СПб ЛЭТИ |
74,4 |
–0,4 |
1,1 |
–0,6 |
–0,5 |
2,1 |
–0,6 |
|
12 |
109 |
Нижегород. гос. НИУ |
73 |
–0,6 |
–0,7 |
0,3 |
–0,4 |
0,0 |
–0,7 |
|
13 |
116 |
Томский политехн. НИУ |
72,4 |
–0,7 |
0,6 |
–0,4 |
0,5 |
–0,0 |
–0,1 |
|
14 |
138 |
Самар. аэрокосм. НИУ |
70,3 |
–0,9 |
0,1 |
0,1 |
–0,4 |
0,8 |
–0,7 |
|
15 |
154 |
Томский гос. НИУ |
69,4 |
–1,0 |
–1,6 |
0,9 |
–0,7 |
–0,6 |
–0,3 |
|
16 |
156 |
Уральский ФУ |
69,4 |
–1,0 |
–1,0 |
–0,5 |
–0,5 |
1,5 |
1,9 |
|
17 |
255 |
Дальневосточный ФУ |
64,6 |
–1,6 |
0,2 |
0,4 |
–0,7 |
0,5 |
0,4 |
Составляющими статистического метода исследования являются корреляционный, факторный, кластерный и дисперсионный анализы. Статистический анализ проводился в системе Statistica [15]. В силу разнородности ПВИ они были стандартизированы.
Результаты проверки ПВИ на корреляционную зависимость (матрица коэффициентов парных корреляций Пирсона r) приведены в табл. 2. Жирным шрифтом выделены значимые корреляции: высоко значимая (на уровне значимости р ≈ 0,000016 < 0,0005) отрицательная между NЕГЭ и NО; статистически значимая (0,005 < р ≈ 0,029 < 0,05) отрицательная между mЕГЭ и NЦ; статистически значимая (0,005 < р ≈ 0,036 < 0,05) положительная между mЕГЭ и NО; слабо значимая (0,005 < р ≈ 0,057 < 0,05) отрицательная между NО и NЦ; слабо значимая (0,005 < р ≈ 0,093 < 0,05) отрицательная между Dm и N.
Таблица 2
Матрица коэффициентов парных корреляций Пирсона r ПВИ
|
mЕГЭ |
Dm |
NЕГЭ |
NО |
NЦ |
N |
|
|
mЕГЭ |
1,00 |
–0,08 |
–0,24 |
0,51 |
–0,53 |
0,03 |
|
Dm |
–0,08 |
1,00 |
0,24 |
–0,31 |
0,30 |
–0,42 |
|
NЕГЭ |
–0,24 |
0,24 |
1,00 |
–0,85 |
–0,04 |
–0,17 |
|
NО |
0,51 |
–0,31 |
–0,85 |
1,00 |
–0,47 |
0,08 |
|
NЦ |
–0,53 |
0,30 |
–0,04 |
–0,47 |
1,00 |
0,02 |
|
N |
0,03 |
–0,42 |
–0,17 |
0,08 |
0,02 |
1,00 |
Наличие корреляционной зависимости ПВИ предполагает использование факторного анализа, основанного на оценках корреляций (факторных нагрузок) между исходными показателями и факторами (или «новыми» показателями) в рамках выбранной факторной модели и позволяет узнать значимость факторов. С помощью факторного анализа построена 3-факторная модель ПВИ ВКВУЗ 2013 года (табл. 3). В табл. 3 жирным шрифтом выделены наиболее значимые (основные) повернутые факторные нагрузки (частные коэффициенты корреляции) показателей на факторы, что позволяет по совокупности этих показателей интерпретировать соответствующие факторы, приписывая им наиболее существенные черты значимых показателей. В нижней строке приведены доли объясненной данным фактором дисперсии исходных показателей, иными словами, весовые коэффициенты факторов. Накопленная дисперсия 3-мя факторами ≈ 80 %.
Таблица 3
Матрица факторной структуры ПВИ ВКВУЗ 2013 года
|
17-ПВИ |
Ф1 |
Ф2 |
Ф3 |
|
mЕГЭ |
0,762 |
0,074 |
0,324 |
|
Dm |
–0,244 |
0,808 |
–0,159 |
|
NЕГЭ |
0,079 |
0,112 |
–0,989 |
|
NО |
0,420 |
–0,079 |
0,886 |
|
NЦ |
–0,932 |
0,113 |
–0,015 |
|
N |
–0,104 |
–0,848 |
0,081 |
|
Доля фактора |
0,284 |
0,235 |
0,317 |
Согласно табл. 3, высокие факторные нагрузки ПВИ распределились по факторам следующим образом.
Фактор Ф1 – составной, характеризуется в основном mЕГЭ и NЦ, связанных отрицательной корреляционной связью (чем больше mЕГЭ, тем меньше NЦ) и дополнительно mЕГЭ и NО, связанных положительной корреляционной связью (чем больше mЕГЭ, тем больше NО). Таким образом, положительная часть Ф1 интерпретируется в основном как mЕГЭ и дополнительно NО, а отрицательная – как NЦ.
Фактор Ф2 – составной, характеризуется Dm и N, связанных отрицательной корреляционной связью (чем больше Dm, тем меньше N). Таким образом, положительная часть Ф1 интерпретируется как Dm, а отрицательная – как N.
Фактор Ф3 – самый весомый (0,317), составной, характеризуется NО и NЕГЭ, связанных отрицательной корреляционной связью (чем больше NО, тем меньше NЕГЭ). Таким образом, положительная часть Ф3 интерпретируется как NО, а отрицательная – как NЕГЭ.
В построенном 3-мерном факторном пространстве {Ф1, Ф2, Ф3} проведена кластеризацию ВКВУЗ. При этом в качестве меры близости выбрано евклидово расстояние, а в качестве правила объединения двух кластеров использован метод Уорда. Методом древовидной кластеризации построено иерархическое дерево (рис. 1). В зависимости от выбора расстояния объединения можно получить соответствующее число кластеров. Так, например, расстоянию объединения, равного 1,5 (красная пунктирная горизонтальная прямая) соответствуют 10 кластеров (К1–К10), расстоянию объединения, равного 4 (зеленая пунктирная горизонтальная прямая), соответствуют 4 кластера (К1 + К3 + К8, К2, К4 + К5 + К6, К7 + К9 + К10). Таким образом, выбор значения связующего расстояния позволяет проводить кластеризацию на любом уровне, то есть строить кластерную модель с любым наперед заданным числом кластеров. При этом, увеличивая расстояния объединения, можно отслеживать динамику объединения кластеров по мере уменьшения степени их однородности. Например, сначала на уровне расстояния объединения 0,7 объединяются близкие по совокупности ПВИ вузы МФТИ и СПбГУ в кластер К1, а затем на уровне расстояния объединения 1,8 к ним присоединяется МГУ, отличающийся от них аномально большим значением N.
Наряду с методом древовидной кластеризации применен также метод K-средних, проводящий классификацию объектов (ВКВУЗ) по заданному количеству кластеров. Алгоритм метода K-средних, перемещая объекты в разные кластеры с целью минимизации изменчивости внутри кластеров и максимизации изменчивости между кластерами, оценивает качество кластеризации ВКВУЗ по каждому фактору посредством параметрического дисперсионного анализа (табл. 3) как сильно значимое (на уровне значимости 0,0005 < р < 0,005).
После оценки качества классификации рассчитываются средние значения показателей по каждому кластеру для оценивания значимости их различий между собой. Графики средних кластеров ВКВУЗ в исходном пространстве ПВИ представлены линейными графиками на рис. 2.
Для каждого ПВИ согласно апостериорному критерию наименьших значений разности (НЗР) выделены однородные (различающиеся незначимо, то есть на уровне значимости р > 0,10) иногда пересекающиеся группы кластеров (рис. 2), расположенные в порядке убывания средних:
Ø mЕГЭ: {К1–К5}, {К5–К8}, {К6–К10}.
Ø Dm : {К4, К6, К7}, {К6, К7, К9, К5}, {К9, К5, К1, К8, К3, К10, К2}.
Ø NО : {К2}, {К5, К3, К1}, {К3, К1, К9, К10, К4, К7, К8, К6}.
Ø NЕГЭ: {К6, К8}, {К8, К1, К3, К4, К9, К5, К10, К7}, {К2}.
Ø NЦ : {К7, К10}, {К4, К9, К8}, {К8, К6, К1, К5, К3, К2}.
Ø N : {К3, К10}, {К2, К1, К9, К8, К7, К5, К4, К6}.
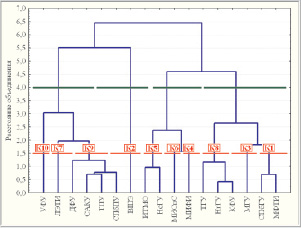
Рис. 1. Дендрограмма ВКВУЗ в пространстве {Ф1, Ф2, Ф3}
Таблица 3
Результаты дисперсионного анализа кластеризации ВКВУЗ по факторам
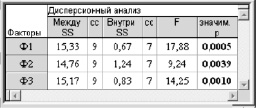
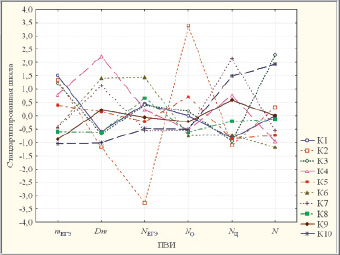
Рис. 2. Линейные графики кластерных средних ВКВУЗ в пространстве ПВИ
Результаты кластерного анализа ВКВУЗ по совокупности показателей (рис. 2) позволяют провести качественную классификацию ВКВУЗ в номинальной шкале измерений, полагая в качестве уровня «Средний» – стандартизированный интервал (–0,5; +0,5) для ПВИ. Аномально высокие значения (> + 2,0) определяют уровень «Лидер», а аномально низкие значения (< –2,0) определяют уровень «Аутсайдер». Промежуточные значения между средними и аномальными определяют уровень «Выше среднего» и «Ниже среднего» соответственно. Монокластеры характеризуются аномальными значениями по некоторым показателям: К2 (ВШЭ) – Лидер по NО и Аутсайдер по NЕГЭ при уровне «Выше среднего» по mЕГЭ, К3 (МГУ) – Лидер по N при уровне «Выше среднего» по mЕГЭ, К4 (МИФИ) – Лидер по Dm, «Ниже среднего» по N при уровне «Выше среднего» по mЕГЭ и NЦ, К7 (ЛЭТИ) – Лидер по NЦ при уровне «Выше среднего» по Dm, К6 (МИСиС) имеет уровень «Выше среднего» по Dm и NЕГЭ, Ниже среднего по N, NО и NЦ при уровне «Средний» по mЕГЭ, К10 (УФУ) имеет уровень «Выше среднего» по N и NЦ при Ниже среднего по mЕГЭ и Dm. Составные кластеры менее выразительны, но тем не менее имеют свои выразительные черты: К1 (МФТИ, СПбГУ) имеет уровень «Выше среднего» по mЕГЭ, К5 (ИТМО, НсГУ) имеет уровень «Средний–Выше среднего» по mЕГЭ и NО при «Ниже среднего» по N и NЦ, К8 (КФУ, НгГУ, ТГУ) имеет уровень «Выше среднего» по NЕГЭ, Ниже среднего по mЕГЭ и Dm при уровне «Средний–Ниже среднего» по NО, К9 (ТПУ, САКУ, СПбПУ, ДФУ) имеет уровень «Средний–Ниже среднего» по mЕГЭ за счет слабого звена ДФУ и уровень «Средний–Выше среднего» по NЦ за счет слабого звена ТПУ.
Результаты подобной кластеризации вузов могут быть учтены в рамках проходящей реформы высшего образования, например, при финансировании вузов или сокращении их количества.
Выводы
1. На основании корреляционного анализа показателей вступительных испытаний в ведущие вузы выявлена высоко значимая наиболее сильная отрицательная корреляционная зависимость между долевым количеством абитуриентов, принятых по конкурсу баллов ЕГЭ и по олимпиадам.
2. В рамках кластерного анализа в 6-мерном пространстве ПВИ построена кластерная модель 17-и ведущих вузов, позволяющая проводить кластеризацию на любом уровне, т.е. строить кластерную модель с любым наперед заданным числом кластеров, что дает возможность выделять группы вузов, однородных по совокупности ПВИ.
3. Подробно рассмотрена высоко значимая 10-кластерная модель. Для каждого показателя выделены группы однородных кластеров. На основе результатов кластеризации проведена качественная классификация ведущих вузов.
Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.
Рецензенты:Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск;
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Работа поступила в редакцию 05.12.2013.
Библиографическая ссылка
Арефьев В.П., Михальчук А.А. КЛАСТЕРИЗАЦИЯ ВЕДУЩИХ КОНКУРЕНТОСПОСОБНЫХ РОССИЙСКИХ ВУЗОВ НА ОСНОВЕ ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ 2013 ГОДА // Фундаментальные исследования. – 2013. – № 10-15. – С. 3456-3461;URL: https://fundamental-research.ru/ru/article/view?id=33085 (дата обращения: 19.04.2024).



