Газовые гидраты – твердые кристаллические соединения, образующиеся при определенных термодинамических условиях из газа и воды [1]. Отличительной особенностью и уникальностью газогидратов является их особое строение, которое позволяет содержать в одном кубическом метре газового гидрата в 180 раз больше газа, чем в свободном состоянии [2, 3]. По оценкам специалистов, значительная часть запасов углеводородного сырья находится в газогидратном состоянии, прогнозные запасы которых огромны [2].
Некоторые закономерности процесса образования газогидрата при инжекции газа в пористую среду, частично насыщенную водой, исследованы в работах [4–7]. В данной работе исследуется математическая модель разложения газогидрата в результате отбора газа из природного пласта, насыщенного газом и гидратом.
Рассмотрим однородный, горизонтальный пласт постоянной толщины и длины L, представляющий собой пористую породу, частично заполненную газогидратом. Кровля и подошва пласта непроницаемы. В пласте пробурена скважина, вскрывшая пласт на всю толщину. Давление р0 и температура Т0 соответствуют условиям стабильного существования гидрата, т.е. T0 < Ts(p0), где Ts(p0) – равновесная температура, соответствующая исходному давлению системы. Будем полагать, что через левую границу пласта (r = r0) происходит отбор газа под давлением ре. При этом температура на ней поддерживается равной значению Те (например, с помощью нагревателя, помещенного в забой скважины). Данные параметры соответствуют условиям разложения гидрата (Те > Ts(pe)) и поддерживаются постоянными в ходе всего процесса диссоциации гидрата.
Рассмотрим случай, когда фазовые переходы идут на фронтальной поверхности. В этом случае вглубь пласта начинает распространяться фронтальная поверхность диссоциации гидрата, разделяющая пласт на две области. В первой (ближней) области гидрат полностью разложился на исходные продукты, поэтому в порах присутствуют только газ и вода, вторая (дальняя) область насыщена газом и гидратом.
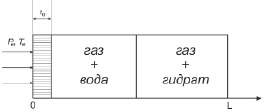
Рис. 1. Постановка задачи
Система уравнений тепло- и массопереноса в осесимметричном случае для ближней и дальней областей описывается следующим образом:
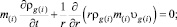 (1)
(1)
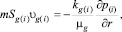 (2)
(2)
где kg – коэффициент абсолютной проницаемости; μg – динамическая вязкость газа.
Газ считаем калорически совершенным:
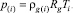 (3)
(3)
Пусть существует граница r = r(n), разделяющая ближнюю и дальнюю области, тогда условия баланса масс (воды и газа) и энергии на ней примут вид:
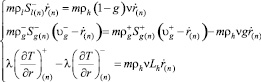 (4)
(4)
Из первого уравнения системы (4) для величины водонасыщенности на границе диссоциации гидрата (со стороны первой области) получим следующее выражение:
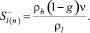 (5)
(5)
Поскольку, согласно принятой модели, вода является неподвижной, последнее выражение также определяет величину водонасыщенности в первой области. Применив закон Дарси (2) к системе (4) получим следующие соотношения для определения основных параметров пористой среды на ней:
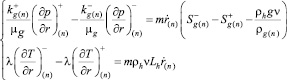 (6)
(6)
Здесь верхние индексы «плюс» и «минус» соответствуют параметрам перед и за фронтом. В частности, для величин газонасыщенности справа и слева от границы фазового перехода имеем следующие выражения:
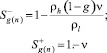
На правой границе пласта (r = L) поставим условия, моделирующие отсутствие потоков массы газа и тепла через нее:
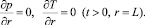 (7)
(7)
Постановка осесимметричной задачи относится к классу нелинейных задач математической физики. Поскольку данные задачи определены в областях с неизвестными подвижными границами фазовых переходов, то для их решения используется метод ловли фронтов в узлы пространственной сетки.
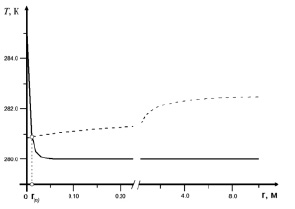
Рис. 2. Распределение температуры при отборе газа под давлением pe = 5 МПа. Сплошная и штриховая линия соответствуют температуре пласта и равновесной температуре
В работе получены решения, описывающие распределения основных параметров в каждой области пласта. В результате анализа полученных решений установлены основные закономерности разложения газогидратов в пористых пластах в зависимости от давления, температуры и гидратонасыщенности пласта, а также в зависимости от интенсивности отбора газа. Получены распределения температур при отборе газа под давлением pe = 5 МПа (рис. 2) и pe = 6 МПа (рис. 3). Как следует из рис. 2, температура пласта перед фронтом диссоциации гидрата выше, а за фронтом — ниже равновесной температуры. Таким образом, решение с фронтальной границей разложения гидрата является термодинамически непротиворечивым. Из рис. 3 следует, что температура пласта за фронтом разложения гидрата поднимается выше равновесной температуры (пунктирная линия). Таким образом, при данных значениях невозможно построить физически непротиворечивую модель с фронтальной границей фазовых переходов вследствие того, что за фронтом происходит перегрев гидрата и его диссоциация на газ и воду.
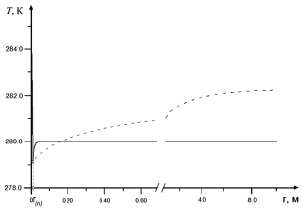
Рис. 3. Распределение температуры при отборе газа под давлением pe = 6 МПа. Сплошная и штриховая линия соответствуют температуре пласта и равновесной температуре
Выводы
В работе получены решения, описывающие распределения основных параметров в каждой области пласта. В результате анализа полученных решений установлены основные закономерности разложения газогидратов в пористых пластах в зависимости от давления и температуры. Получены распределения температур при отборе газа под давлением pe = 5 МПа и pe = 6 МПа.
Рецензенты:
Гималтдинов И.К., д.ф.-м.н., профессор, заведующий кафедрой «Прикладная математика и механика» Стерлитамакского филиала, ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак;
Мустафина С.А., д.ф.-м.н., профессор, заведующая кафедрой «Математическое моделирование», декан физико-математического факультета Стерлитамакского филиала ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.
Работа поступила в редакцию 25.12.2013.
Библиографическая ссылка
Кильдибаева С.Р. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ОТБОРА ГАЗА ИЗ ПОРИСТОЙ СРЕДЫ, ЧАСТИЧНО НАСЫЩЕННОЙ ГАЗОВЫМ ГИДРАТОМ // Фундаментальные исследования. – 2013. – № 11-6. – С. 1163-1166;URL: https://fundamental-research.ru/ru/article/view?id=33269 (дата обращения: 18.04.2024).



