Вырождающиеся эллиптические уравнения представляют собой один из важных разделов современной теории дифференциальных уравнений с частными производными. Такие уравнения имеют многочисленные приложения в газовой динамике, теории малых изгибаний поверхностей вращения, безмоментной теории оболочек и др.
Пусть 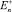 – полупространство xn > 0 евклидова пространства En точек x = (x1, x2, ..., xn). Пусть G – конечная область в
– полупространство xn > 0 евклидова пространства En точек x = (x1, x2, ..., xn). Пусть G – конечная область в 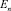 , симметричная относительно плоскости xn = 0 и ограниченная поверхностью G. Обозначим через
, симметричная относительно плоскости xn = 0 и ограниченная поверхностью G. Обозначим через 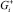 часть G, расположенную в
часть G, расположенную в 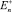 . Граница области G+ разбивается G(0) и G+, расположенные соответственно на плоскости xn = 0 и в полупространстве xn > 0. Поверхность G+ является поверхностью класса Λm,B, когда G ∈ Λm [3]. Через
. Граница области G+ разбивается G(0) и G+, расположенные соответственно на плоскости xn = 0 и в полупространстве xn > 0. Поверхность G+ является поверхностью класса Λm,B, когда G ∈ Λm [3]. Через 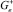 обозначим область
обозначим область 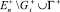 ,
, 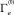 – ее граница, расположенная на плоскости xn = 0.
– ее граница, расположенная на плоскости xn = 0.
Рассмотрим внутреннюю (внешнюю) краевую задачу: найти четное по xn решение уравнения
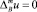 (1)
(1)
в области 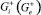 , (2m – 1) раз непрерывно дифференцируемое в
, (2m – 1) раз непрерывно дифференцируемое в 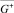 и удовлетворяющее граничным условиям
и удовлетворяющее граничным условиям
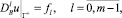
и в случае внешней задачи удовлетворяющее на бесконечности условиям, обеспечивающим ее единственность. Здесь 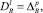 , если l = 2p и
, если l = 2p и 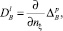 , если l = 2p + 1, nξ – внешняя нормаль к границе G+ в точке ξ,
, если l = 2p + 1, nξ – внешняя нормаль к границе G+ в точке ξ, 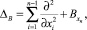 ,
, 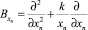 – оператор Бесселя, k – любое положительное число, m > 2. Уравнение вида (1) назовем В-полигармоническим уравнением.
– оператор Бесселя, k – любое положительное число, m > 2. Уравнение вида (1) назовем В-полигармоническим уравнением.
Известно [2], что фундаментальные решения уравнения (1) с особенностью в начале координат имеют вид
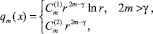
где 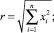 γ = n + k.
γ = n + k.
Значения 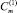 и
и 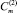 выберем таким образом, чтобы
выберем таким образом, чтобы
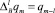 (2)
(2)
и
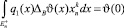 (3)
(3)
для любой четной по xn бесконечно дифференцируемой и финитной в 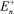 функции ϑ(x).
функции ϑ(x).
Можно проверить, qm удовлетворяет условиям (2) и (3) при следующих значениях 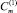 и
и 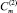 :
:
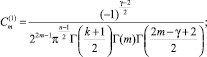
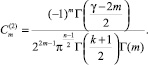
С помощью непосредственного подсчета получаем, что
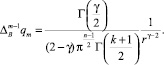
Для получения фундаментального решения с особенностью в произвольной точке ξ применим к функции qm(x) оператор обобщенного сдвига 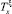 [4]:
[4]:
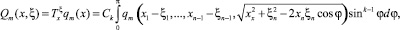
где 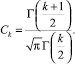
Так как операторы 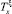 и ΔB коммутируют, то в силу формальной самосопряженности оператора
и ΔB коммутируют, то в силу формальной самосопряженности оператора 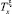 из формулы (3) следует, что
из формулы (3) следует, что
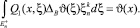
Пусть u и ω четные по xn функции класса  . Тогда имеют место тождества
. Тогда имеют место тождества
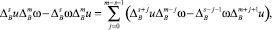 (4)
(4)
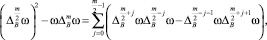 (5)
(5)
при четном m, и
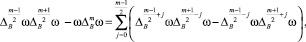 (6)
(6)
когда m – нечетное число.
Нам понадобятся, для четных по xn функций 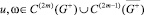 , первая формула Грина
, первая формула Грина
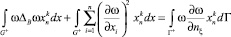 (7)
(7)
и вторая формула Грина
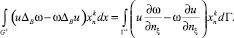 (8)
(8)
Интегрируя обе части тождеств (4), (5), (6) по области G+ и пользуясь формулой (8) получим обобщенные формулы Грина
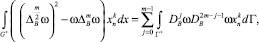 (9)
(9)
для всех четных m и
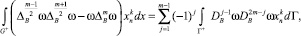 (10)
(10)
когда m – нечетное число, а также имеет место формула
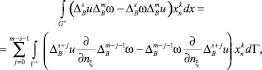
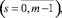 (11)
(11)
где 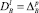 , если l = 2p и
, если l = 2p и 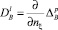 , если l = 2p + 1, nξ – внешняя нормаль к границе G+ в точке ξ.
, если l = 2p + 1, nξ – внешняя нормаль к границе G+ в точке ξ.
Теорема. Задача (1), (2) в классе 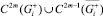 не может иметь более одного решения.
не может иметь более одного решения.
Доказательство. Пусть ω(x) – разность двух предполагаемых решений. Тогда эта функция в области 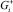 удовлетворяет уравнению (1), на границе G+ однородным краевым условиям
удовлетворяет уравнению (1), на границе G+ однородным краевым условиям
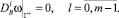 (12)
(12)
Очевидно, что
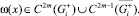
Пусть m – четное число. В силу формулы (9) и условий (12) следует, что
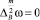 в G+ (13)
в G+ (13)
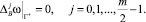 (14)
(14)
С помощью первой формулы Грина (7) можно установить, что задача (13), (14) имеет только нулевое решение, то есть ω ≡ 0.
Пусть теперь m – нечетное число. С учетом (10) и начальных условий (12), будем иметь
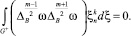
Таким образом, получили две задачи
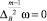 в G+
в G+
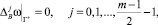
и
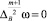 в G+,
в G+,
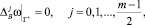
которые аналогичны задаче (13), (14) следовательно ω ≡ 0. Теорема доказана.
Как было показано в работе [1], имеют место следующие интегральные представления для решения уравнения (1):
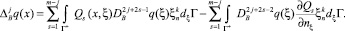 (15)
(15)
Отсюда при j = 0 имеем, что
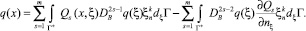
Введем в рассмотрение потенциалы
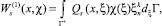
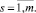 (16)
(16)
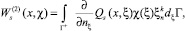
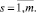
Формулу (15) с помощью этих потенциалов можно записать в виде
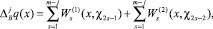 (17)
(17)
в том числе при j = 0
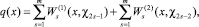 (18)
(18)
где 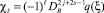 для всех
для всех 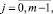
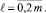 C помощью перенумерации потенциалы в формуле (18) расположим в порядке возрастания индексов их плотностей. В результате мы имеем
C помощью перенумерации потенциалы в формуле (18) расположим в порядке возрастания индексов их плотностей. В результате мы имеем
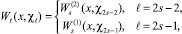 (19)
(19)
где 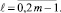 . Тогда формулы (17) и (18) примут вид
. Тогда формулы (17) и (18) примут вид
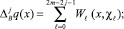 (20)
(20)
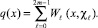 (21)
(21)
Выпишем формулы скачка потенциалов Wℓ(x, χℓ)
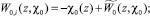
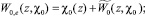
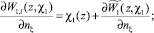
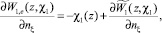
при этом z ∈ G+, индекс i – означает предел из 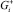 ; e – предел из
; e – предел из 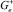 , волна – прямое значение. Отсюда и из формулы (2) следует
, волна – прямое значение. Отсюда и из формулы (2) следует
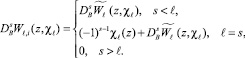
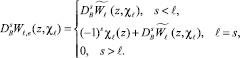
Заключение
В работе исследуются краевые задачи для В-полигармонического уравнения 2m-порядка в n-мерном случае. Доказывается единственность поставленных задач. Строятся потенциалы и даны формулы скачков для этих потенциалов, необходимые для сведения краевой задачи к системе интегральных уравнений.
Рецензенты:
Мухлисов Ф.Г., д.ф.-м.н., профессор, кафедра высшей математики и математического моделирования, Казанский (Приволжский) федеральный университет, г. Казань;
Сушков С.В., д.ф.-м.н., профессор, зав. кафедрой теории относительности и гравитации, Казанский (Приволжский) федеральный университет, г. Казань;
Кульбачинский В.А., д.ф.-м.н., профессор, кафедра физики низких температур и сверхпроводимости, физический факультет, Московский государственный университет им. М.В. Ломоносова, г. Москва;
Бичурин М.И., д.ф.-м.н., профессор, заведующий кафедрой ПТРА, Новгородский государственный университет, г. Нижний Новгород.
Работа поступила в редакцию 30.12.2013.
Библиографическая ссылка
Денисова М.Ю., Киндер М.И. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДНОГО СИНГУЛЯРНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С ОПЕРАТОРОМ БЕССЕЛЯ // Фундаментальные исследования. – 2013. – № 11-7. – С. 1328-1332;URL: https://fundamental-research.ru/ru/article/view?id=33339 (дата обращения: 23.04.2024).



