Состояние вопроса и постановка задачи исследований
Создание новых математических моделей и методов для информационных систем анализа, управления и обработки информации является актуальным, поскольку повышает эффективность системного анализа в целом и ускоряет оперативность принятия решений в них. В качестве недостатка существующих в настоящее время систем следует отметить то, что по причине стремительного роста научно-технического процесса в области компьютерных технологий, современные инновационные технологии используются не в полной мере в существующем оборудовании. Последнее обстоятельство объясняется тем, что технический прибор был создан до появления того или иного программного обеспечения, способа моделирования или конкретной технологии и по этой причине или вообще не способен работать с данным пакетом программ, типом моделирования, или не всегда достаточно поддерживает скорость обработки информации.
Направления исследований
В работах [1,2] были определены недостатки в существующих информационных системах (далее ИС), приводящие к неэффективному анализу техногенных систем (далее ТС) и определены направления дополнительных исследований, сформулированы задачи работы по направлениям повышения эффективности работы ИС, среди которых:
а) увеличение объема поступающего информационного потока для анализа за счет максимальной загруженности каналов;
б) разработки новых математических методов обработки информации применительно к распространению техногенных загрязнений. Созданные ИС [3–6] предусматривают введение дополнительных блоков под постоянно действующие модели и новое программное обеспечение в существующие подсистемы анализа и обработки информации.
Разработка новых методов и моделей. На основе проведенного мониторинга информационного обеспечения предприятия [7–10] по существующим показателям информационной системы были построены гистограммы, по которым определили средние значения исследуемых параметров и произвели оценку дисперсии. В результате исследований установили нормальный закон распределения средних значений и с целью устранения недостатков по надежности обеспечения системы видами техногенной информации в зависимости от временного интервала сформулировали оптимизационную модель, приведенную ниже.
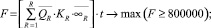
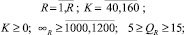
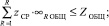
1 ≤ Zср ≤ 5; ZОБЩ ≤ 1000,
где R – территориальная единица (промышленный объект); Q – вес заявки (от 5 до 15 кб); 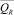 – среднее значение веса заявки из R-го объекта; K – число действующих каналов (от 40 до 160); KR – число действующих каналов на R-м объекте; ∞R – среднее значение числа заявок из R-го объекта, проходящих по 1 действующему каналу (от 1000 до 1200) за определенный интервал времени (1 ч) – интенсивность потока заявок; ∞RОБЩ – общее значение числа заявок из R-го объекта, ∞R ОБЩ = KR∙∞R; t – временной интервал в течение которого исследуется процесс наполнения системы информацией (1 ч); zСР – средние затраты на извлечение одной заявки из R-го объекта (от 1 до 5 копеек); ZОБЩ – консолидированные средства для информационной системы (1000000 копеек).
– среднее значение веса заявки из R-го объекта; K – число действующих каналов (от 40 до 160); KR – число действующих каналов на R-м объекте; ∞R – среднее значение числа заявок из R-го объекта, проходящих по 1 действующему каналу (от 1000 до 1200) за определенный интервал времени (1 ч) – интенсивность потока заявок; ∞RОБЩ – общее значение числа заявок из R-го объекта, ∞R ОБЩ = KR∙∞R; t – временной интервал в течение которого исследуется процесс наполнения системы информацией (1 ч); zСР – средние затраты на извлечение одной заявки из R-го объекта (от 1 до 5 копеек); ZОБЩ – консолидированные средства для информационной системы (1000000 копеек).
Процесс наполнения системы анализа, управления и принятия решений потоками от исследуемых объектов происходит следующим образом (рис. 1). С объекта RR за определенный интервал времени t по действующим информационным каналам KR неограниченной пропускной способности поступают заявки ∞R различного объема QR содержащие данные по производственному процессу. Система считается загруженной и способной эффективно осуществлять анализ и управление при загрузке ее не менее 800000, и экономически эффективной, если средние затраты на извлечение информации по одной заявке zСР умноженные на интенсивность поступления информации по всей системе, будут меньше консолидированных средств ZОБЩ, потраченных для создания системы на R-х объектах.
На рис. 1 приведена схема наполнения системы анализа управления и принятия решений (далее САУПР) потоком заявок, поступающих по действующим каналам связи от объекта R1, в котором по каналам 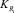 , информация с интенсивностью
, информация с интенсивностью 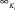 (значение числа заявок, проходящих канал за интервал времени) поступает в систему для последующего анализа. В работе системы определены следующие направления целевой функции и ограничения работы:
(значение числа заявок, проходящих канал за интервал времени) поступает в систему для последующего анализа. В работе системы определены следующие направления целевой функции и ограничения работы:
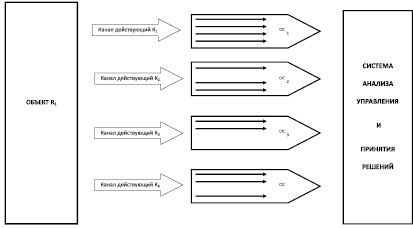
Рис. 1. Схема наполнения САУПР потоком заявок, поступающих по действующим каналам связи от объекта R
1) на заданном интервале времени целевая функция стремится к максимуму, чтобы процесс информационного обеспечения не прекращался, каналы, обеспечивающие систему информацией были загружены, и интенсивность поступления информации была максимальна.
2) для любого канала, вида информации, территориальной единицы справедливо условие:
– средние затраты на извлечение информации, умноженные на интенсивность поступления информации, должны быть меньше консолидированных средств, для информационной системы (в расчетном случае меньше 1000000 копеек).
– число каналов, обеспечивающих систему информацией, не должно быть равно нулю;
– интенсивность поступления информации не должна быть равна нулю.
Результаты исследований и их обсуждение. Для решения оптимизационной модели применялся метод Монте-Карло, результаты расчета которого для отдельного R-го объекта по оптимизации наполнения системного архива за определенный интервал времени (1 ч) представлены в табл. 1, а по оптимизации экономической эффективности системы в табл. 2.
Таблица 1
Результаты расчета методом Монте-Карло наполнения системы информацией из R-го объекта
|
№ п/п |
|
KR – число действующих каналов на R-м объекте |
∞R – среднее значение числа заявок из R-го объекта |
t – временной интервал (1 ч) |
F – целевая функция |
Выполняется ли условие по максимальному наполнению системы информацией? |
|
От 5 до 15 |
От 40 до 160 |
от 1200 до 1000 |
1 |
max (F ≤ 8000000) |
||
|
1 |
9,4 |
74,2 |
1087,2 |
1 |
757 999 |
Нет |
|
2 |
13,1 |
79,7 |
1071,6 |
1 |
1 116 197 |
Да |
|
3 |
11,2 |
102,3 |
1046,0 |
1 |
1 193 862 |
Да |
Таблица 2
Результаты расчета методом Монте-Карло экономической эффективности системы для R-го объекта
|
№ п/п |
zСР – средние затраты на извлечение одной заявки из R-го объекта (копеек) |
KR – число действующих каналов на R-м объекте |
∞R – среднее значение числа заявок из R-го объекта |
F – целевая функция |
Выполняется ли условие по экономической эффективности системы? |
|
От 1 до 5 |
От 40 до 160 |
от 1000 до 1200 |
max (F ≤ 1000000) |
||
|
1 |
3,4 |
144,3 |
1101,6 |
534 327 |
Да |
|
2 |
2,7 |
102,1 |
1120,3 |
311 850 |
Да |
|
3 |
2,8 |
148,0 |
1042,9 |
429 645 |
Да |
На представленной ниже гистограмме представлена вероятность распределения данных по диапазонам значений, с учетом технических требований, при которых минимальный рост объема системного архива в час составляет 400000 байт, максимальный не превосходил 2000000 байт, а оптимальный находился в пределах от 800000 до 1600000 байт.
Работая по вышеописанной схеме модель позволяет наполнять систему необходимым объемом информации о технологических и техногенных параметрах, увеличивая эффективность анализа и обработки информации системой, на основании, которого осуществляется поддержка принятия решений при управлении промышленным предприятием или комплексом предприятий в зависимости от поставленных перед САУПР задач.
Заключение
Разработанная оптимизационная модель положена в основу наполнения информацией системы анализа, управления и принятия решений принцип действия которой подробно изложен в литературе [1, 2]. Применение модели повышает эффективность анализа обработки информации, качество и надежность работы системы и вносит значительный вклад в математическое обеспечение систем анализа, оптимизации, управления, принятия решений и обработки информации.
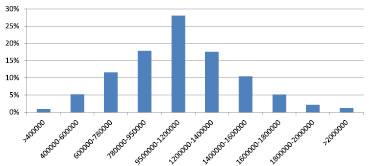
Рис. 2. Гистограмма распределения вероятности числа работающих каналов, необходимых для создания оптимального объема системного архива
Рецензенты:
Сорокер Л.В., д.т.н., профессор, Научно-производственный комплекс «Югцветметавтоматика», г. Владикавказ;
Каменецкий Е.С., д.ф.-м.н,. заведующий отделом математического моделирования, ФГБУН «Южный математический институт ВМЦ РАН РСО-А», г. Владикавказ.
Работа поступила в редакцию 18.02.2014.
Библиографическая ссылка
Петров Ю.С., Соколов А.А. РАЗРАБОТКА НОВЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ И МЕТОДОВ ДЛЯ СИСТЕМНОГО АНАЛИЗА ИНФОРМАЦИИ // Фундаментальные исследования. – 2014. – № 3-3. – С. 480-483;URL: https://fundamental-research.ru/ru/article/view?id=33699 (дата обращения: 25.04.2024).




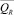 среднее значение веса заявки из R-го объекта
среднее значение веса заявки из R-го объекта