Известны нелинейно-оптические методы исследования кинетических коэффициентов жидких двухкомпонентных сред, основанные на исследовании самовоздействия излучения [4–7, 10] или характеристик динамических голограмм [8, 11]. В обоих случаях механизм оптической нелинейности среды обусловлен перераспределением концентрации компонент в неоднородном световом поле и соответствующем изменении показателя преломления среды.
В ряде работ исследован термодиффузионный механизм нелинейности, обусловленный термодиффузией молекул (эффект Соре) или наночастиц в жидкостях [1–6]. При этом изменение коэффициента поглощения среды обычно не учитывается. В случае различающихся коэффициентов поглощения компонент изменение их концентрации приводит также к изменению коэффициента поглощения среды (просветлению или потемнению), что может быть использовано для определения коэффициента термодиффузии [9, 12–15].
Целью данной работы является теоретическое и экспериментальное исследование термодиффузионного механизма самоиндуцированного просветления двухкомпонентной среды лазерным пучком.
Материалы и методы исследования
Схема эксперимента показана на рис. 1. В качестве источника излучения использовался He-Ne лазер мощностью 60 мВт (длина волны излучения – 0,63 мкм). Пространственное распределение температуры фиксировалось термографом «IRTIS 2000» с параметрами: чувствительность на 30–0,05 °С; диапазон измерений –40...+200 °С; точность измерения – ±1 %; пространственное разрешение – 2 мрад; поле зрения камеры – 25×20 град; разрешение кадра – 256×256; время сканирования – 1,5 с.
Эксперименты проводились с двумя типами кювет: толстостенными – толщина стенок 2,25 мм, и тонкостенными – толщина стенок 0,125 мм. В обоих случаях толщина слоя среды составляла 30 мкм. В качестве двухкомпонентной среды использовалась суспензия частиц сажистого углерода (диаметром 0,1... 0,2 мкм) в воде.
Результаты исследования и их обсуждение
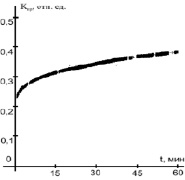
При освещении горизонтальной кюветы с суспензией пучком излучения с радиусом 1,8 мм в результате действия термодиффузии в области пучка происходило уменьшение концентрации дисперсной фазы и, соответственно, коэффициента поглощения среды – самоиндуцированное просветление (СИП). Фотография области просветления показана на рис. 2(а). Зернистость изображения обусловлена разрешением цифрового фотоаппарата. На рис. 2(б) приведена термограмма кюветы с бинарной средой, демонстрирующая радиально симметричное распределение температуры поверхности кюветы. На рис. 2(г) приведена зависимость температуры среды в центре лазерного пучка от времени. Видно, что просветление среды в центре пучка приводит к уменьшению ее температуры. Таким образом впервые экспериментально продемонстрирована отрицательная обратная связь, обусловленная термодиффузией поглощающих частиц, на возможность которой впервые было указано в теоретической работе [14].
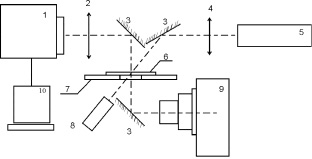
Рис. 1. Схема установки: 1 – термограф ИРТИС-200; 2 – инфракрасный объектив; 3 – зеркало; 4 – фокусирующая линза; 5 – гелий-неоновый лазер; 6 – кювета; 7 – опора кюветы; 8 – фотодиод; 9 – фотоаппарат с микрообъективом; 10 – компьютер
 а
а 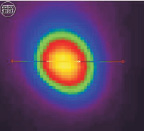 б
б
 в
в 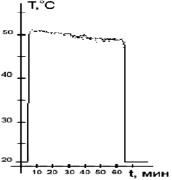 г
г
Рис. 2. a – фотография области просветления; б – термограмма области просветления; в – изменение коэффициента пропускания просветленного участка в процессе экспозиции; г – зависимость температуры поверхности кюветы в центре пучка от времени
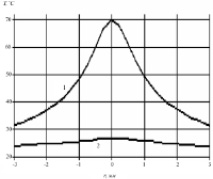
Пространственное распределение температуры в установившемся режиме приведено на рис. 3, а. Видно, что из-за низкого теплового сопротивления толстой кюветы в центре пучка она прогревается слабее, что приводит к меньшему градиенту температуры в плоскости слоя среды и, соответственно, к меньшему изменению коэффициента пропускания. Аналогичная зависимость прослеживается и в динамике изменения коэффициента пропускания кювет с разной толщиной стенок (рис. 3, б).
 а
а 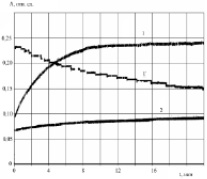 б
б
Рис. 3. а – радиальный профиль температуры поверхности кюветы в области просветления; б – зависимость от времени интегрального коэффициента пропускания кюветы, толщина стенок кюветы: кривая 1 – 0,125 мм (1′ – восстановление коэффициента пропускания при уменьшении мощности пучка в 20 раз); кривая 2 – 2,25 мм
Кривая 1′ показывает процесс восстановления коэффициента пропускания тонкой кюветы при уменьшении мощности пучка лазера в 20 раз. Время восстановления соответствует диффузионному (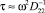 ), время просветления (для кривой 1) несколько меньше из-за различия механизмов просветления и восстановления, а также из-за наличия отрицательной обратной связи по поглощаемой мощности, уменьшающей время просветления.
), время просветления (для кривой 1) несколько меньше из-за различия механизмов просветления и восстановления, а также из-за наличия отрицательной обратной связи по поглощаемой мощности, уменьшающей время просветления.
Теоретическая модель явления
Рассмотрим двухкомпонентную жидкофазную среду, коэффициент поглощения которой α целиком определяется одним компонентом с концентрацией С (α = βС, где β = (∂α/∂С) – константа среды). Для гауссова пучка распределение интенсивности падающего излучения в плоскости слоя I = I0exp(–r2/ω2), где ω – радиус пучка; r – расстояние от оси пучка. Пусть среда находится в тонкой кювете толщиной (d + 2L) << ω (рис. 4). Система балансных уравнений для концентрации С и теплового потока состоит из уравнений тепло- и массопереноса [2]:
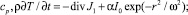 (1)
(1)
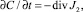 (2)
(2)
где cp, ρ – удельные теплоемкость и плотность среды; T – температура среды; J1 и J2 – тепловой и концентрационный потоки соответственно:
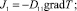 (3)
(3)
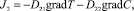 (4)
(4)
где D11 – коэффициент теплопроводности среды; D22 – коэффициент диффузии поглощающих частиц; D21 – коэффициент термодиффузии наночастиц.
В стационарном режиме, считая, что для малых толщин слоя среды d и окна кюветы L (d, L << ω) можно пренебречь радиальным (вдоль r) тепловым потоком, получаем из (1), (3) одномерную тепловую задачу:
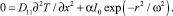 (5)
(5)
Граничные условия соответствуют конвективному теплообмену на границе раздела окно кюветы‒воздух:
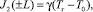 (6)
(6)
где γ, T0 – соответственно коэффициент конвективного теплообмена и температура внешней среды, Tг = T(L + d/2). Для температуры среды в центре кюветы из (5)–(6) получаем:
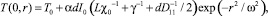 (7)
(7)
где χ0, D11 – коэффициенты теплопроводности материала окон кюветы и двухкомпонентной среды соответственно. Для толщин слоя d << L можем пренебречь изменением температуры в слое среды по толщине кюветы и принять ее равной T(0). В установившемся режиме (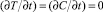 ) из (4) имеем для распределения концентрации Cs:
) из (4) имеем для распределения концентрации Cs:
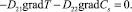 (8)
(8)
Интегрируя (8) по объему кюветы с учетом сохранения числа частиц и выражения (7), получаем:
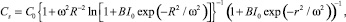 (9)
(9)
где 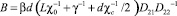 ; C0 – начальная концентрация частиц; R – внутренний радиус цилиндрической кюветы.
; C0 – начальная концентрация частиц; R – внутренний радиус цилиндрической кюветы.
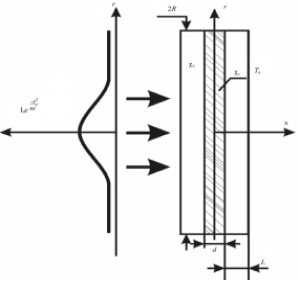
Рис. 4. К расчету термодиффузионного просветления двухкомпонентной среды в тонкослойной цилиндрической кювете
Полученные выражения позволяют определить кинетические коэффициенты среды из экспериментальных данных о параметрах наведенного излучением просветления. В частности, время установления концентрации наночастиц соответствует диффузионному.
Термодиффузионную постоянную определяем из стандартной формулы для установившегося распределения концентрации [2]:
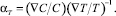 (10)
(10)
Из экспериментальных данных (pис. 2, 3) можно получить величину αT = 0,8 ± 0,025, что соответствует характерным величинам для наночастиц в жидкости [2, 15].
Выводы
Приведенные результаты показывают, что в двухкомпонентной среде с поглощающими частицами термодиффузия может приводить к значительной величине самоиндуцированного просветления среды под действием пространственно ограниченного оптического пучка. Поэтому самоиндуцированную модуляцию коэффициента поглощения необходимо учитывать при анализе концентрационных нелинейностей бинарных смесей [2, 11–13], а также в методах оптической диагностики наносред, в частности, в термолинзовой спектроскопии многокомпонентных сред [3].
Рецензенты:
Карпец Ю.М., д.ф.-м.н., профессор кафедры физики, профессор кафедры «Автоматика, телемеханика и связь», ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения», г. Хабаровск;
Криштоп В.В., д.ф.-м.н., профессор кафедры физики, профессор кафедры «Физика и теоретическая механика», ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения», г. Хабаровск.
Работа поступила в редакцию 11.04.2014.
Библиографическая ссылка
Доронин И.С., Иванова Г.Д., Кузин А.А., Окишев К.Н. ТЕРМОДИФФУЗИЯ НАНОЧАСТИЦ В ЖИДКОСТИ // Фундаментальные исследования. – 2014. – № 6-2. – С. 238-242;URL: https://fundamental-research.ru/ru/article/view?id=34141 (дата обращения: 19.04.2024).



