Начиная с классических работ Френкеля и Шоттки, число работ по электронной и ионной проводимости чистых кристаллов, кристаллов с дефектами и твердых растворов, включая природные минералы, росло значительными темпами. Несмотря на достигнутые успехи в понимании многих процессов в твердых электролитах [1–5], новые модели, описывающие ряд мало исследованных явлений и, в частности, размерные эффекты, будут, на наш взгляд, полезными. Такая модель рассматривается в настоящей работе.
Дефекты кристалла (вакансии, примесные ионы и т.д.) будем рассматривать как систему невзаимодействующих частиц, погруженную в термостат. Квантовые переходы, обусловленные взаимодействием дефектов с термостатом, будут диссипативными (с вероятностью Р) в отличие от взаимодействия с внешним полем (с вероятностью F). Диссипативные процессы приводят к тому, что вторичное поле (отклик системы) всегда меньше первичного, вызывающего образование дефектов.
Поскольку подсистема дефектов обменивается с термостатом только энергией, то соответствующий им ансамбль частиц будет каноническим. В этом случае выражение для статистической энтропии имеет вид
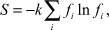
где fi – функция распределения; k – постоянная Больцмана. Дифференцируя по времени и преобразуя, получим:
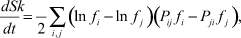
где Pij – вероятность перехода из начального i (с энергией Ei) в возбужденное состояние j (с энергией Ej).
Для диссипативных процессов принцип детального равновесия имеет вид
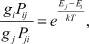
где gi, gj – статистические веса для уровней Ei и Ej.
Каноническая функция распределения:
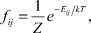
где статистическая сумма: Z = e–G/kT, G – потенциал (свободная энергия) Гиббса системы термостат + система дефектов.
Положим, что не конфигурационная часть потенциала Гиббса линейно зависит от концентрации N дефектов:
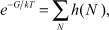
где h(N) = ω(N)∙e–G/kT; ω(N) – статистический вес.
Опуская промежуточные вычисления, находим
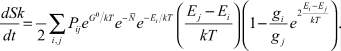
Пренебрегая малыми членами и заменяя сумму интегралом получим:
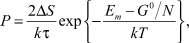
где ΔS – изменение энтропии в диссипативном процессе; Em – среднее значение энергии основного состояния дефектов; τ – время релаксации.
Для функции отклика Ф системы на внешнее поле имеем:
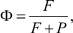
где Р – вероятность диссипативного процесса; F определяет вероятность перехода в возбужденное состояние за счет первичного внешнего поля, причем F = 1/τр, где τр – время жизни возбужденного состояния. Тогда имеем:
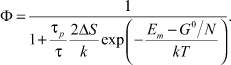
Обозначая предэкспоненциальный множитель через С, получим:
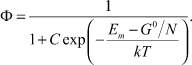(1)
Рассмотрим сначала гомогенную изотропную среду, которая содержит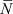 
электронов проводимости и характеризуется термодинамическим потенциалом Гиббса G° Возникновение тока плотностью j в среде является откликом системы невзаимодействующих электронов на внешнее поле и имеет вид (1), где Em = eE, e – заряд электрона.
После линеаризации (1) при Φ = j (в скалярном виде), получаем:
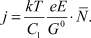(2)
Когда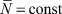 
, мы из (2) имеем закон Ома в дифференциальной форме:
j = σE;
где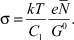 
(3)
Проводимость s связана с удельным сопротивлением r соотношением:
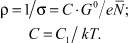(4)
Константа С1 характеризует процесс перехода системы электронов из возбужденного состояния в основное и примерно одинакова для многих веществ. Таким образом, гетерогенность твердых растворов будет сказываться на ее электропроводности через энергию Гиббса G°.
Поскольку, как известно,
G° = H – TS + PV, (5)
где Н – энтальпия; Т – температура; S – энтропия; V – объем, то при C = const из (5) следует, что
ρ/ρ0 = β∙P/P0, (6)
где P0 – атмосферное давление; β – некоторая константа. Из (6) следует линейная зависимость удельного сопротивления от давления. Действительно, как показано на рис. 1 для CaSO4, график относительного удельного сопротивления хорошо аппроксимируется линейной функцией [6].
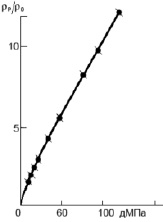
Рис. 1. Изменение удельного сопротивления CaSO4 под действием всестороннего давления [6]
Температурная зависимость электропроводности твердых растворов имеет сложную форму из-за температурной зависимости практически всех параметров, входящих в выражение (4). Ситуация упрощается, поскольку в реальных и практически важных случаях наблюдается, как правило, один тип проводимости. В случае электролитов выражение (4) дает:
ρ = A/kT, (7)
где А – некоторая константа.
Формула (7) показывает гиперболическую зависимость электропроводности электролитических твердых растворов, аналогичную эмпирической зависимости [6]. В случае, когда твердые растворы представляют собой диэлектрики или полупроводники, то в (4) следует положить концентрацию зарядов N, равной
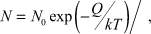
где Q – энергия активации. Из формулы (4) тогда следует:
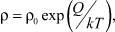
что соответствует классическим теориям.
На рис. 2 показана зависимость σ = 1/ρ в логарифмическом масштабе для измеренных нами твердых растворов
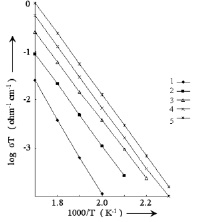
Рис. 2. Зависимость logσ(T) от 1000/T для твердых электролитов:
1 – K2SO4 + 3,8 mol % BaSO4; 2 – K2SO4 + 3,8 mol % SrSO4; 3 – K2SO4 + 3,8 mol % CaSO4;
4 – K2SO4 + 3,8 mol % MgSO4; 5 – K2SO4 + Li2SO4:Li2CO3
В случае идеальных твердых растворов
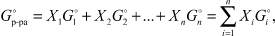(8)
где Xi – мольная концентрация i-й компоненты, причем
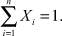
Из (4) и (8) вытекает, что для сложной (гетерогенной) среды
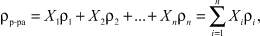. (9)
Из (9) следует, что без дополнительной информации о средних значениях содержания различных компонентов в твердом растворе найти корреляционную связь между содержанием искомого компонента и ρр-ра практически невозможно. В случае, когда компонента X1 >> X2 >> ... >> Xn, то можно установить корреляционную связь между r и концентрацией компонента X1 на основе выражения (4).
В случае бинарного твердого раствора из (9) следует:
ρр-ра = X1ρ1 + X1ρ2.
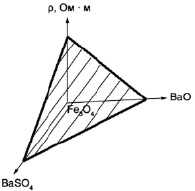
На рис. 3 в качестве примера показана зависимость ρр-ра от соотношения компонент в бинарной смеси Fe3O4-BaO, а на рис. 4 - для системы Fe3O4-BaO-BaSO4.
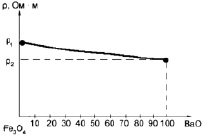
Рис. 3. Зависимость ρр-ра от соотношения компонент в системе Fe3O4–BaO
Перепишем уравнение (3) в виде
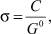(10)
где С = const.
Изменение радиуса зерна минерала приводит к изменению давления P на межфазной границе, описываемому уравнением Кельвина:
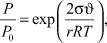(11)
где r – радиус зерна; σ – межфазное поверхностное натяжение; ϑ – молярный объем зерна; P0 – давление над плоской поверхностью; R – универсальная газовая постоянная.
Поскольку
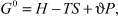(12)
то (10), с учетом (11) и (12), примет вид
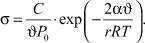(13)
Обозначая D = C/υP0, разлагая (13) в ряд и ограничиваясь первыми двумя членами, получим:
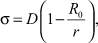(14)
где «критический радиус» R0 равен
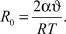
Уравнение (14) можно переписать следующим образом:
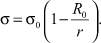(15)
Таким образом, мы получили уравнение (15), описывающее зависимость электропроводности от размера зерна твердого раствора. Критический радиус R0, при котором электропроводность обращается в ноль, определяется поверхностным натяжением или поверхностной энергией. В случае жидкостей эти две величины совпадают. В случае твердых тел – нет, и связь между ними дается уравнением Шаттльворта и Херинга [7]:
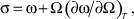
где Ω – площадь поверхности твердого тела; ω – поверхностная энергия.
Для диэлектрической проницаемости, проводя аналогичные рассуждения, мы получаем уравнение подобное (15):
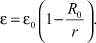(16)
Уравнения (15) и (16) хорошо описывают экспериментально наблюдаемое поведение диэлектрической проницаемости и электрической проводимости.
Обобщенная зависимость электрических параметров кристаллов и твердых растворов показана на рис. 5.
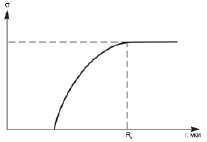
Рис. 5. Обобщенная зависимость электропроводности от размера зерна твердого раствора
Уравнения (15) и (16) позволяют по экспериментальным данным определять поверхностное натяжение твердых растворов.
Экспериментальное определение поверхностного натяжения твердых тел затруднено тем, что их молекулы (атомы) лишены возможности свободно перемещаться. Исключение составляет пластическое течение металлов при температурах, близких к точке плавления [7]. Недавно нами предложено 3 метода экспериментального определения поверхностного натяжения твердых тел – диэлектриков и магнитных материалов [8–10].
Выводы
Предложенная нами термодинамическая модель, как показано выше, позволяет прогнозировать поведение вновь синтезированных твердых растворов в различных условиях и внешних воздействиях. Уравнения (15) и (16) позволяют по экспериментальным данным определять поверхностное натяжение кристаллов и твердых растворов. Поверхностные явления имеют место в любой гетерогенной системе, состоящей из двух или нескольких фаз. По существу весь материальный мир – гетерогенен. Как гомогенные можно рассматривать системы лишь в ограниченных объёмах пространства. Поэтому роль поверхностных явлений в природных и технологических процессах чрезвычайно велика.
Рецензенты:
Арефьев К.П., д.ф.-м.н., профессор, заведующий кафедрой высшей математики Национального исследовательского Томского политехнического университета, г. Томск;
Градобоев А.В., д.т.н., начальник лаборатории специспытаний ОАО «Научно-исследовательский институт полупроводниковых приборов», г. Томск.
Работа поступила в редакцию 07.05.2014.
Библиографическая ссылка
Халенов О.С., Юров В.М., Коровкин М.В. ТЕРМОДИНАМИЧЕСКИЕ АСПЕКТЫ ЭЛЕКТРИЧЕСКОЙ ПРОВОДИМОСТИ КРИСТАЛЛОВ И ТВЕРДЫХ РАСТВОРОВ // Фундаментальные исследования. – 2014. – № 6-7. – С. 1384-1388;URL: https://fundamental-research.ru/ru/article/view?id=34346 (дата обращения: 16.04.2024).