В настоящее время стационарная работа вибрационных установок происходит в малоэффективной зарезонансной зоне, в которой мощность двигателя и масса дебаланса завышены в несколько раз. Известно, что амплитуды колебаний в резонансных машинах и устройствах с дебалансным вибровозбудителем в режимах холостого хода и малых нагрузок достигают значительных величин, вызывая в силовых системах этих устройств недопустимо высокие разрушающие механические напряжения [1, 2, 5]. При этом частота вращения ротора может резко измениться. Это скачкообразное изменение частоты приводит к скачкообразному изменению амплитуды и частоты колебаний самого тела (эффект Зоммерфельда), в системе проявляется динамическая неустойчивость периодических режимов движения. Увеличение относительного демпфирования (0,1–0,3) сужает зоны неустойчивости, а дальнейшее увеличение до 0,4–0,6 приводит к полному исчезновению эффекта Зоммерфельда (рис. 1) [4]. Это рождает мысль о возможности создания регулируемых систем электроприводов (СЭП), позволяющих осуществлять их работу с минимальными энергозатратами в околорезонансном режиме при стабилизации требуемых параметров колебаний в условиях вариации технологической нагрузки от номинальной до режима холостого хода. Идея работы заключается в обеспечении работы вибрационных установок в околорезонансном режиме при стабилизации амплитуды колебаний размещением точки номинального режима на линейной части механической характеристики частотно-управляемого асинхронного электропривода с ω0 = (0,95 – 0,98)p, при относительной диссипации системы 2n/p = 0,4 – 0,5, а при снижении технологической нагрузки от 2n/p = 0,4 – 0,5 до 2n/p = 0,2 – 0,1 – снижением ω0 в соответствии с регулировочной характеристикой.
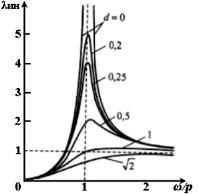
Рис. 1. АЧХ электромеханической системы с инерционным возбуждением
При составлении математической модели электромеханической колебательной системы с частотно-управляемым асинхронным электроприводом инерционного возбуждения (рис. 2) приняты следующие допущения: упругие элементы линейные; электромагнитные переходные процессы не учитываются ввиду малости времени их протекания по сравнению с периодом механических колебаний; силы трения в подшипниках и при движении платформы отсутствуют; потери энергии в электроприводе определяются КПД электродвигателя; колебания платформы m1 – симметричные; сопротивление технологической нагрузке определяется коэффициентом вязкого трения μ [1, 2, 6, 7, 8].
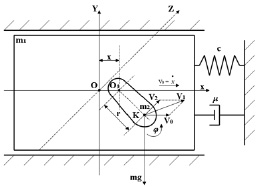
Рис. 2. Расчетная схема электромеханической колебательной системы
Принимая за обобщенные координаты q1 = x и q2 = φ, уравнения Лагранжа 2-го рода примут вид [1, 2, 5, 6, 7, 9]:
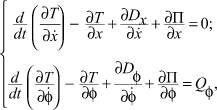(1)
где Т – кинетическая энергия системы; П – потенциальная энергия системы; D – диссипативная функция (функция сопротивления среды) принимается пропорциональной скорости (вязкое трение).
Выполняя операции дифференцирования и преобразования, система уравнений (1) примет вид [1, 2, 5, 9]
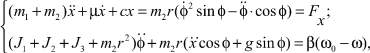(2)
где m1, m2 – масса платформы и инерционного вибровозбудителя соответственно (кг); r – расстояние от оси подвеса до центра тяжести точки K инерционного возбудителя (эксцентриситет) (м); c – коэффициент жесткости упругих элементов подвески ЭМС (Н/м); μ – коэффициент сил сопротивления среды (вязкого трения) (Н·с/м); J1, J2 и J3 – момент инерции ротора двигателя, лепестковой муфты и инерционного возбудителя соответственно (кг·м2); g – ускорение свободного падения (м/c2);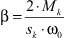 
– коэффициент жесткости механической характеристики, Mk – критический момент электродвигателя (Н·м), sk – критическое скольжение [1, 2, 4, 5].
Многие авторитетные исследователи вибрационной механики сходятся во мнении, что электромагнитный момент электропривода инерционного возбудителя может быть представлен линейной частью статической механической характеристики электродвигателя [1, 2, 4].
Моделирование производится путем решения дифференциальных уравнений и логических выражений (имитационное моделирование) ЭМС с частотно-управляемым асинхронным электроприводом инерционного возбуждения при работе в симметричном режиме на персональном компьютере в приложении Simulink, входящего в пакет прикладных программ MATLAB. При моделировании с использованием Simulink реализуется принцип визуального программирования, в соответствии с которым из библиотеки стандартных блоков создается модель системы и осуществляется расчет. Процесс построения модели в Simulink представляет последовательность выбора необходимых блоков из соответствующих библиотек и соединение их связями [3, 8].
Для блок-схемы имитационной модели систему уравнений (2) целесообразно представить в виде
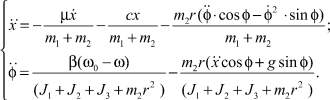(3)
При моделировании приняты расчетные номинальные динамические и технологические параметры разомкнутых систем ЭМС 1 (оклорезонансный режим) и ЭМС 2 (зарезонансный режим) (таблица).
Динамические и технологические номинальные параметры электромеханических систем
|
№ п/п |
Параметры электромеханической колебательной системы в зависимости от частоты: |
ЭМС 1 |
ЭМС 2 |
|
1. |
Собственная частота ЭМС p, с–1 |
157 (25 Гц) |
98,9 (15,7 Гц) |
|
2. |
Номинальная частота вращения инерционного вибровозбудителя ω, с–1 |
150 |
150 |
|
3. |
Амплитуда перемещения x, м |
0,005 |
0,005 |
|
4. |
Принятая работа сил сопротивления среды за период (в резонансном режиме) W = 100, Дж |
||
|
5. |
sin α, где α – угол отставания вынужденных колебаний от возмущающей силы |
0,96 |
0,4 |
|
6. |
Коэффициент эквивалентного вязкого трения μ, Н·с/м |
8600 |
8600 |
|
7. |
Коэффициент жесткости упругого элемента с, Н/м |
3360000 |
2270000 |
|
8. |
Возмущающая сила F, Н |
6600 |
15000 |
|
9. |
Радиус инерционного вибровозбудителя r, м |
0,1 |
0,1 |
|
10. |
Масса инерционного возбудителя m2, кг |
3 |
7,5 |
|
11. |
Работа за период внешних сил W, Дж |
104 |
250 |
|
12. |
Мощность внешних сил P, Вт |
2488 |
5970 |
|
13. |
Кратность потребляемой мощности в зарезонансных режимах |
1,04 |
2,4 |
Имитационная модель ЭМС с частотно-управляемым асинхронным электроприводом инерционного вибровозбудителя по уравнениям (3) в приложении Simulink Matlab (рис. 3) включает в себя следующие структуры.
Структура I – моделирует движения инерционного возбудителя с АД (нижняя строчка системы уравнений (3)), где Jsum = (J1 + J2 + J3 + m2·r2) – суммарный момент инерции роторной части.
Структура II – уравнение перемещения твердого тела (платформы) системы (верхняя строчка системы уравнений (3)).
Структура III – формирование электромагнитного момента асинхронного частотно-управляемого электродвигателя, где ω0 = 150 – частота вращения электромагнитного поля статора, β – коэффициент жесткости механической характеристики с номинальным скольжением равным s = 1 %.
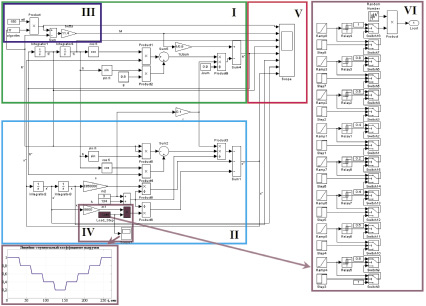
Рис. 3. Блок-схема имитационной модели электромеханической колебательной системы с частотно-управляемым асинхронным электроприводом инерционного возбуждения
Структура IV – моделирование сил сопротивления среды, где h = μ – коэффициент вязкого трения. Блок (Load_Step) – SubSystem (Подсистема) – используется для создания подсистемы из множества блоков в один с целью экономии места на рабочем поле Simulink.
Структура V – блок Scope (осциллограф), выводит графики исследуемых сигналов в функции времени, позволяет наблюдать за изменениями сигналов в процессе моделирования, отображает влияние динамических параметров ЭМС на динамические процессы.
Структура VI – задание режимов работы сил сопротивления среды (технологической нагрузки) (Load_Step). Предназначен для исследования и разработки алгоритмов управления и стабилизации амплитуды колебаний при малых коэффициентах диссипации. Производит 20 %-й линейно-ступенчатый сброс и увеличение силы сопротивления движению платформы, каждые 30 секунд машинного времени, что позволяет выполнять переход нагрузки с одной на другую по линейной функции, при этом в расчете не возникают бесконечные переходные процессы как при скачкообразном сбросе нагрузки [3, 8].
Блок универсален как для симметрично-нагруженных, так и несимметрично-нагруженных ЭМС с частотно-управляемым асинхронным электроприводом инерционного возбуждения.
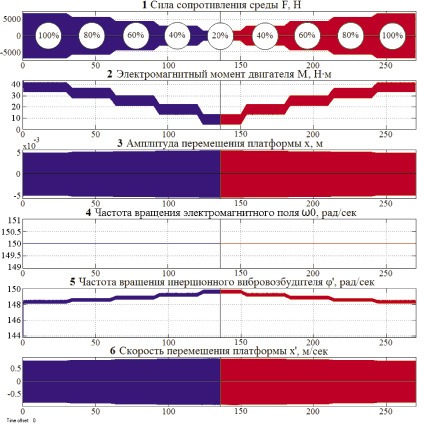
На осциллограммах (рис. 4, а) представлены процессы в ЭМС 1 при работе в околорезонансной зоне (p = 157 c–1, ω = 150 c–1). Здесь на рис. 4, а – 1 – ступенчато изменяемая технологическая нагрузка от номинальной (от 100 %) до режима холостого хода (до 20 %) путём соответственного изменения эквивалентного коэффициента μ вязкого трения. На рис. 4, а – 2 – электромагнитный момент электродвигателя, соответствующий технологической нагрузке рис. 4, а – 1. На рис. 4, а – 3 – амплитуда колебаний платформы заданной величины, полученная изменением частоты вращения электромагнитного поля ω0 электродвигателя рис. 4, а – 4. Скорость перемещения платформы (рис. 4, а – 5) изменяется незначительно при изменении технологической нагрузки от номинальной (от 100 %) до режима холостого хода (до 20 %).
При снижении технологической нагрузки μн (рис. 1, 4, а – 1) увеличивается скорость и амплитуда колебаний платформы. Для стабилизации амплитуды колебаний платформы необходимо снижать скорость ω0 (снижать частоту напряжения преобразователя частоты) в соответствии с регулировочной характеристикой, под которой понимается зависимость угловой скорости вращения электромагнитного поля электродвигателя ω0 от электромагнитного момента электродвигателя при заданном значении амплитуды колебаний платформы во всём диапазоне изменения технологической нагрузки от номинальной до режима холостого хода.
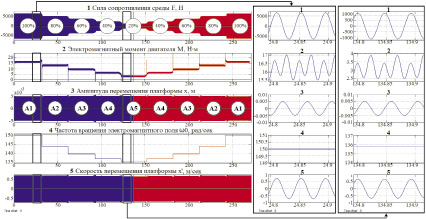а
б
Рис. 4. а – осциллограммы процессов в ЭМС 1 при работе в околорезонансной зоне (p = 157 c–1, ω = 150 c–1); б – осциллограммы процессов в ЭМС 2 при работе в зарезонансной зоне (p = 98,9 c–1, ω = 150 c–1)
Для построения регулировочной характеристики (рис. 5) с точками A1, A2, A3, A4, A5, в которых значение амплитуд равно заданному, а электромагнитный момент соответствует уровню технологической нагрузки, положения точек ω02, ω03, ω04, ω0хх определяются с помощью имитационной модели ЭМС путём изменения (снижения) вручную указанных скоростей до уровня, на котором амплитуды имеют заданное значение (рис. 4, а – 3). Полученная характеристика (рис. 5) позволит получать эффективные алгоритмы стабилизации амплитуды колебаний платформы в околорезонансной зоне при изменении технологической нагрузки от номинальной до режима холостого хода.
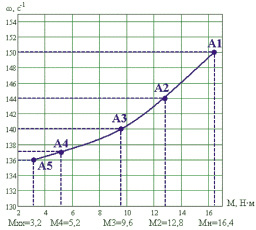
Рис. 5. Регулировочная характеристика
При работе ЭМС в зарезонансной зоне (рис. 4, б) не требуется автоматизированных систем управления электроприводом, так как в этом случае амплитуда перемещения платформы мало чувствительна к изменению технологической нагрузки (относительного коэффициента демпфирования). Однако кратность потребляемой мощности в зарезонансном режиме в 2,4 раза выше по отношению к мощности, потребляемой в резонансном режиме (таблица).
Существенное влияние на равномерность вращения дебалансного возбудителя оказывает суммарный момент инерции (J1 + J2 + J3 + m2·r2) роторной части. При моделировании установлено, что при доведении суммарного момента инерции до 0,7–0,9 кг·м2 путём увеличения J2 лепестковой муфты отклонение от средней скорости вращения инерционного возбудителя не превышает 0,2 рад/с. В этом случае в первом приближении скорость вращения инерционного возбудителя может быть принята постоянной [5].
Имитационная модель электромеханической колебательной системы с частотно-управляемым асинхронным электроприводом инерционного возбуждения позволяет:
1. Корректировать динамические параметры исследуемых колебательных систем для получения заданных кинематических и энергетических характеристик этих систем с погрешностью не более 5 %.
2. Проводить сравнительный анализ эффективности работы электромеханических колебательных систем в околорезонансной, резонансной и зарезонансной зонах:
а) при условии равенства выполняемых работ;
б) при равных амплитудах перемещения платформы;
в) при различных и равных собственных частотах систем;
г) при различных видах сил сопротивления среды (сил вязкого, сухого трений, случайной величины).
3. Строить регулировочные характеристики для работы в околорезонансных режимах при условии стабилизации амплитуды колебаний платформы на заданном уровне.
4. Исследовать режимы работы электромеханической колебательной системы с частотно-управляемым асинхронным электроприводом инерционного возбуждения:
а) симметричный режим (заданные значения работ выполняются при движении платформы в одну и другую сторону – грохоты, вибростенды и т.д.);
б) несимметричный режим (работы выполняются на рабочем ходе платформы за половину периода – вибрационные щековые дробилки, вибротранспорт и др.).
5. Проводить анализ эффективности работы разомкнутых и замкнутых систем электроприводов инерционных вибровозбудителей.
6. Разрабатывать эффективные алгоритмы стабилизации амплитуды перемещения платформы электромеханической колебательной системы с частотно-управляемым асинхронным электроприводом инерционного возбуждения при вариациях технологической нагрузки от номинальной до нагрузки холостого хода при работе в околорезонансной зоне.
Выводы
- Разработанная имитационная модель электромеханической колебательной системы в приложении Simulink MATLAB позволяет строить регулировочные характеристики для работы в околорезонансных режимах при условии стабилизации амплитуды колебаний платформы на заданном уровне.
- Установлено, что при увеличении суммарного момента инерции до 0,7–0,9 кг·м2 путём увеличения момента инерции лепестковой муфты изменение от средней скорости вращения инерционного возбудителя не превышает 0,2 рад/с, что позволяет в первом приближении принять скорость вращения инерционного возбудителя неизменной величиной.
- Сравнительный анализ режимов работы (таблица) показал, что режим работы в околорезонансной зоне (в пределах (0,85–0,97) ω/p) является близким к оптимальному по энергопотреблению (кратность по отношению к потреблению в резонансном режиме –1,04).
- Работа в зарезонансной зоне (в пределах (1,41–1,56) ω/p) сопровождается увеличенным электропотреблением в 2,0–2,5 раза соответственно по сравнению с режимом работы в околорезонансной зоне.
Рецензенты:
Шклярский Я.Э., д.т.н., профессор кафедры «Электротехника, электроэнергетика, электромеханика», Национальный минерально-сырьевой университет «Горный», г. Санкт-Петербург;
Проскуряков Р.М., д.т.н., профессор кафедры «Электротехника, электроэнергетика, электромеханика», Национальный минерально-сырьевой университет «Горный», г. Санкт-Петербург.
Работа поступила в редакцию 28.05.2014.
Библиографическая ссылка
Загривный Э.А., Дубовик Д.В. ИМИТАЦИОННАЯ МОДЕЛЬ ЭЛЕКТРОМЕХАНИЧЕСКОЙ КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ С АСИНХРОННЫМ ЭЛЕКТРОПРИВОДОМ ИНЕРЦИОННОГО ВИБРОВОЗБУДИТЕЛЯ // Фундаментальные исследования. – 2014. – № 8-3. – С. 570-576;URL: https://fundamental-research.ru/ru/article/view?id=34596 (дата обращения: 25.04.2024).