Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кожухова В.Н. 1

---

1 Димитровградский инженерно-технологический институт – филиал ФГАОУ ВПО «Национальный исследовательский ядерный университет «МИФИ»

В статье рассмотрен вопрос прогнозирования динамики демографических показателей на примере общего коэффициента смертности населения развитых стран. Из известных методов на основе динамических, имитационных и регрессионных моделей выбран параметрический подход к эконометрическому моделированию временных рядов. Обосновано выделение тренда и циклической компоненты в динамике анализируемых показателей. Предложены семь моделей трендов на основе логистических кривых: обобщения логистических моделей Рамсея, Ферхюльста и Гомпертца. Обосновано применение нового критерия точности прогноза – критерия Н.Г. Загоруйко – для падающей динамики тренда. На примере динамики смертности США и Швейцарии разработаны параметрические модели, построены прогнозы на 27 и 38 лет вперед соответственно. Определен уровень смертности в развитых странах на ближайшие 30–40 лет. Разработанный инструментарий может быть применен для прогнозирования других демографических показателей, в том числе для Российской Федерации.

Статья в формате PDF

561 KB

демография

коэффициент смертности

моделирование

прогнозирование

логистическая кривая

1. Кожухова В.Н. Методики исследования точности идентификации временных рядов на примере моделей с логистическим трендом и аддитивной стохастической компонентой / Е.В. Семенычев, В.Н. Кожухова // Вестник Поволжского государственного университета сервиса. Серия «Экономика». – 2013. – № 2(28). – С. 148–153.

2. Кожухова В.Н. Методы идентификации логистической динамики и жизненного цикла продукта моделью Верхулста / В.К. Семенычев, В.Н. Кожухова, Е.В. Семенычев // Экономика и математические методы. – 2012. – Т. 48, Вып. 2. – С. 108–115.

3. Кожухова В.Н. Разработка и исследование комплекса моделей логистической динамики социально-экономических показателей: автореф. дис. ... канд. экон. наук. – Оренбург, 2013. – 25 с.

4. Кормановская И.Р. Моделирование сценария демографического развития Новгородской области до 2030 года / И.Р. Кормановская, Л.И. Бернасовская, Е.В. Птицина // Проблемы современной экономики. – 2012. – № 3(43). – С. 224–228.

5. Семёнычев В.К. Анализ и предложения моделей экономической динамики с кумулятивным логистическим трендом: монография / В.К. Семенычев, В.Н. Кожухова. – Самара: Изд-во «СамНЦ РАН», 2013. – 152 с.

6. Index Mundi. Country Facts [Электронный ресурс]. – Режим доступа: http://www.indexmundi.com/ (дата обращения: 06.07.2014).

7. Modis T. Predictions – 10 years later. – Geneva: Growth Dynamics, 2002. – 322 p.

При математическом моделировании демографических процессов наиболее часто применяются динамические, имитационные и регрессионные модели, описанные в работах отечественных ученых С.П. Капицы, Ю.М. Плотинского, С.Ю. Малкова, А.А. Саградова и др. Большинство моделей касается численности населения региона, страны или мира в целом, в то время как моделей рождаемости, смертности, ожидаемой продолжительности жизни предложено меньше [4]. Регрессионные модели этих показателей, как правило, строятся на основе временных рядов применением какой-либо нелинейной функции тренда (логарифмической, экспоненциальной, степенной).

В работах зарубежных ученых, например [7], отмечается, что динамика подобных показателей носит логистический характер и описывается S-образными кривыми, а применение экспоненциальных кривых некорректно. Так, ожидаемая продолжительность жизни в развитых странах представляет собой растущую логистическую кривую, смертности – падающую. Прогнозы ожидаемой продолжительности жизни и численности населения на основе растущей логистической кривой осуществлялись Р. Перлом, А. Грюблером, Т. Модисом, П. Майером и др. Оценка параметров логистической модели с уменьшающимися абсолютными значениями тренда (для падающей кривой) является нетривиальной задачей, поскольку получение прогноза при стремлении показателя к нулю требует других моделей, методов их идентификации и новых показателей точности прогноза.

Цель исследования. В настоящей работе поставлена цель продемонстрировать применение предложенного комплекса параметрических эконометрических моделей с логистическим характером тренда, показать возможность получения прогнозов демографических показателей смертности населения.

Материал и методы исследования

Использована статистика общего коэффициента смертности в развитых странах мира (в статье показаны примеры США и Швейцарии, однако исследование включало и множество других стран). Использование зарубежной статистики связано с недостаточностью исходной статистической информации для Российской Федерации (особенно с тем фактом, что Россия лишь недавно встала на путь снижения смертности населения). Таким образом, предлагаемые модели разработаны «на перспективу» их применения для России.

Общий коэффициент смертности представляет собой отношение числа умерших людей за год в стране к средней численности населения за год и, как правило, рассчитывается на 1000 чел. населения (в ‰). Динамика общего коэффициента смертности с развитием цивилизации, в частности медицины, снижается, стремясь к некоторому пределу.

Известно, что логистическая кривая условно представляет собой три стадии роста: ускоряющуюся экспоненциальную, линейную и замедляющуюся экспоненциальную [5].

Доступные выборки статистических данных включают в себя линейную и замедляющуюся экспоненциальную стадии логистической кривой, которая стремится к уровню спада – нижней горизонтальной асимптоте. Для США известны данные 1930–2012 гг. (83 наблюдения), для Швейцарии – 1900–2013 гг. (114 наблюдений) [6].

Рассмотренный комплекс моделей трендов падающей логистической динамики включал следующие модели [5]:

1) модель Рамсея с константой

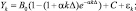
2) трехпараметрическая модель Рамсея

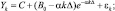
3) четырехпараметрическая модель Рамсея

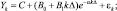
4) обобщенная модель Ферхюльста

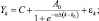
5) модель Ричардса

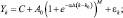
6) модель Гомпертца с левой асимметрией

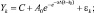
7) модель Гомпертца с правой асимметрией

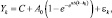
где Y_k – фактические значения временного ряда; k = 1, ..., n – номера наблюдений; n – объем выборки; ε_k – стохастическая компонента; Δ – период дискретизации (месяц, квартал, год и т.д.); C, A₀, B₀, B₁, α, k₀, M – параметры моделей.

Циклическая компонента может присутствовать во временных рядах и моделироваться суммой r гармоник

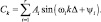
Все предложенные модели нелинейны по параметрам. Оценивались параметры с помощью методов:

а) конструирования обобщенных параметрических ARMA-моделей с помощью Z-преобразования для моделей 1–3, а также моделей циклической компоненты;

б) численного решения МНК методом Левенберга ‒ Марквардта для модели 4 [2];

в) алгоритма RPROP (из теории нейронных сетей) для моделей 5–7.

Данные методы показали вычислительную устойчивость при их тестировании на искусственно сгенерированных выборках [1].

В качестве критерия точности моделирования используется коэффициент (индекс) детерминации R2, а для точности прогнозирования ‒ критерий Н.Г. Загоруйко [3]:

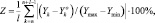
где l – горизонт прогноза; – рассчитанные по модели значения ряда; Ymax, Ymin – максимальное и минимальное значения в выборке соответственно.

Данный критерий применяется потому, что при анализе моделей с падающим трендом на тестовых выборках была продемонстрирована некорректность применения таких общепринятых показателей, как MAPE-оценка и второй коэффициент Тейла, для оценки точности прогноза. Критерий Н.Г. Загоруйко обладает большей универсальностью и точностью: он дает сопоставимые результаты как для растущего, так и для падающего трендов. Показано, что для достоверных прогнозов значение критерия Н.Г. Загоруйко для падающих кривых не должно превышать 10 %, что соответствует рекомендованному значению второго коэффициента Тейла в 20 % для растущих кривых [3].

Для оценки точности прогноза исходный ряд показателя разбивался на две части: рабочую и контрольную. Для построения модели использовались данные рабочей части, а по контрольной рассчитывались значения показателя точности прогноза. В контрольную часть выносилась 1/3 исходной выборки – 27 последних наблюдений для США и 38 последних наблюдений для Швейцарии. Предполагается, что в будущем будет получена точность прогноза того же порядка. Для формирования окончательной модели контрольная выборка вновь объединялась с рабочей.

Для сравнения моделей и обоснования выбора лучшей по адекватности модели из комплекса предложенных применялся скорректированный критерий Акаике, штрафующий за увеличение числа параметров.

Результаты исследования и их обсуждение

Предварительный анализ данных показал, что структура временного ряда для общего коэффициента смертности одинакова и носит аддитивный характер:

,

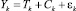выделяются тренд T_k и циклическая компонента C_k. Наличие циклической компоненты было подтверждено анализом стохастической компоненты после элиминирования тренда, а также анализом автокорреляционной функции рядов. Период дискретизации Δ принят равным 1. Для каждого случая был выбран наилучший тренд в соответствии с тремя критериями (таблица).

Результаты расчета критериев точности моделирования и прогнозирования для семи логистических трендов

Наилучший тренд по трем критериям для США – трехпараметрическая модель Рамсея. Для Швейцарии картина не столь однозначна: два тренда показали примерно одинаковую точность. В данном случае рекомендовано выбрать тренд с меньшим числом параметров. На основе выделения тренда для развитых стран (в том числе и на других примерах) можно сказать, что трехпараметрическая модель Рамсея лучше других отражает динамику смертности. Вид моделей трендов:

для США

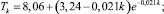
для Швейцарии

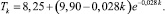
Циклическая компонента представляет собой одну гармонику с постоянной амплитудой:

для США

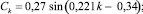
для Швейцарии

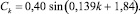
Циклическая компонента отражает колебания в динамике смертности с периодом в 28 лет для США, 40 лет – для Швейцарии.

Рассчитанные критерии точности моделирования и прогнозирования для итоговых моделей оказались высокими: R² = 0,963; Z = 3,06 % для США, R² = 0,943; Z = 5,04 % для Швейцарии. На рисунке, а и б, представлены результаты моделирования динамики общего коэффициента смертности для США и Швейцарии соответственно.

а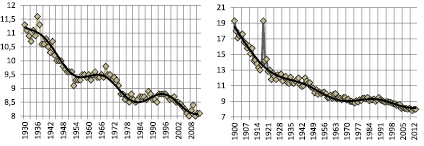б

Моделирование динамики общего коэффициента смертности на 1000 чел. населения в США (а) и Швейцарии (б), ‰

Прогнозируемые по модели уровни спада составили 8,06 и 8,25 для США и Швейцарии соответственно. Коэффициент α ≈ 0,02 для обоих стран показывает темп выбытия населения. Таким образом, в ближайшие 30–40 лет на современном этапе развития медицины среднегодовая смертность стабилизируется на уровне 8 чел. на 1000 чел. населения развитых стран. Также получены прогнозные значения по годам на 27 лет вперед для США и 38 лет вперед для Швейцарии.

Заключение

Предложенный комплекс моделей может быть применен и для иных демографических показателей, если целью исследователя ставится задача построения параметрической модели. В работе [1] на примере ожидаемой продолжительности жизни предложен метод получения интервальных оценок точности прогноза для моделей с логистическим трендом с помощью генерации тестовых выборок. Такой метод позволяет получить не только основной прогноз развития показателя, но и его пессимистический и оптимистический варианты.

В случае достаточности статистических данных разработанные эконометрические модели и методы их идентификации могут быть применены и для демографических показателей Российской Федерации.

Рецензенты:

Семенычев В.К., д.э.н., д.т.н., профессор, ректор, МБОУ ВО «Самарская академия государственного и муниципального управления», г. Самара;

Ильмушкин Г.М., д.п.н., к.ф.-м.н., профессор, заведующий кафедрой высшей математики, Димитровградский инженерно-технологический институт – филиал ФГАОУ ВПО «Национальный исследовательский ядерный университет «МИФИ», г. Димитровград.

Работа поступила в редакцию 23.07.2014.

Библиографическая ссылка