Вопросы определения точности местоположения абонента с помощью спутниковых навигационных систем (СНС) изучены в настоящее время довольно подробно. Однако недостаточно внимания уделяется этим вопросам в условиях плохой видимости антенной навигационного приемника участка небесной поверхности. Подобная ситуация может возникнуть как преднамеренно, например, при скрытном определении местоположения, так и случайно, например, при аварийной посадке летательного аппарата. Как указано в [1, 4], определяемая с помощью СНС точность дается в значении «минимального возможного уровня» – то есть не хуже определенного уровня за определенный промежуток времени. Для любой точки земной поверхности точность в горизонтальной плоскости эквивалентна или лучше, чем 100 метров, исходя из среднеквадратической ошибки измерения расстояния. Это значит, что за период времени в 24 часа плановые координаты, определяемые с помощью GPS, будут находиться не дальше чем в 100 метрах от истинных координат на протяжении 95 процентов времени наблюдений. Соответствующая точность определения высот – 156 метров, а для времени – 340 наносекунд.
Эти расчётные параметры точности определены для орбитальной группировки из 24-х спутников при маске возвышения 5 градусов без препятствий и как минимум четырёх наблюдаемых спутников с геометрическим фактором потери точности позиционирования (PDOP) не более шести. Это означает, что в зависимости от местоположения или времени суток реальная точность GPS будет меняться. В глубоких каньонах городов мы можем столкнуться с тем, что в поле зрения не будет и четырех спутников или PDOP наблюдаемых спутников станет значительно больше шести.
Целью настоящего исследования является статистическая оценка влияния параметров смешанной спутниковой группировки GPS-Глонасс на точность определения координат в условиях городских каньонов. Для оценки точности были проведены измерения с использованием экспериментального GPS-Глонасс приемника, созданного на основе интегрального модуля S3535G2F компании SkyTraq [6], внешний вид которого показан на рис. 1.

Рис. 1. Внешний вид GPS-Глонасс приемника
Кроме навигационного модуля на плате размещены источник питания LT1086 – 3.3 и драйвер COM-порта ADM3202JRN. Процесс проектирования и настройки приемника подробно описан в [2]. Плата навигационного модуля подключена к внешнему источнику питания, соединена с COM-портом компьютера соединительным кабелем, через высокочастотный разъем к ней подключена выносная Глонасс/GPS антенна 2J433GFD-500RG174-C20N фирмы 2J.
Антенна закреплена на внутренней стороне окна лаборатории. Окно лаборатории, находящейся на первом (цокольном этаже) 4-этажного здания, направлено на юго-запад.
Большая часть окна затенена стоящим в непосредственной близости (примерно 1 метр) металлическим зданием. На окне установлена металлическая решетка. Таким образом, область видимого антенной свободного пространства в азимутальной плоскости составляет примерно 70 градусов.
Результаты исследования и их обсуждение
Измерения координат производились на протяжении нескольких дней с различными временными промежутками – от 15 до 60 минут. В качестве программы, обрабатывающей и визуализирующей сообщения GPS-Глонасс приемника, была использована Geos Demo, разработчик программы – КБ «ГеоСтар навигация» [5]. Программа удобна тем, что позволяет отображать местоположение абонента на картах Google, скриншоты данного окна программы были использованы для оценки точности (рис. 2).
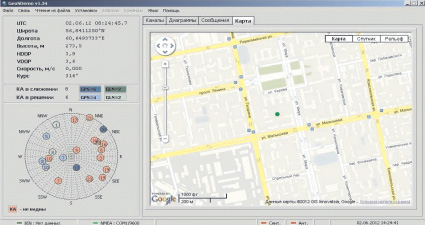
Рис. 2. Скриншот программы Geos Demo с указанием объекта на карте Google
В результате поставленных экспериментов было получено 91 измерение, в каждом из которых присутствовали следующие данные: координаты местоположения, отмеченные на карте, высота точки над уровнем моря, геометрические показатели потери точности (HDOP, VDOP), количество спутников, участвующих в решении. Поскольку эти данные получены под влиянием большого числа случайных факторов (наблюдаемое количество спутников зависит от затененности антенны приемника, геометрические показатели определяются по наблюдаемой случайной группировке спутников, присутствие возможных помех искажает сигнал), можно считать их статистическим протоколом. Исследуем полученные результаты наблюдений статистическими методами.
При статистической обработке данных использовалась программа Statgraphics Centurion 15.2.11.0 ([3]). Статистически исследовались свойства и взаимодействие следующих случайных факторов: количество спутников, участвующих в решении; геометрические показатели потери точности: HDOP, VDOP, 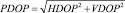 ; расчетные координаты в горизонтальной плоскости (X, Y) местоположения антенны приемника в метрах в некоторой системе координат; отклонение
; расчетные координаты в горизонтальной плоскости (X, Y) местоположения антенны приемника в метрах в некоторой системе координат; отклонение 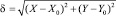 расчетного местоположения приемника (X, Y) от реального (X0, Y0).
расчетного местоположения приемника (X, Y) от реального (X0, Y0).
Измерение координат местоположения осуществлялось по карте скриншотов программы Geos Demo в декартовой системе координат, заданной улицами Гагарина – Малышева (адрес здания, где проводился эксперимент). Учитывая масштаб, погрешность измерений составила примерно 10–15 метров. Фрагмент протокола измерений представлен в табл. 1.
Таблица 1
Фрагмент протокола измерений
|
№ п/п |
Спутники |
HDOP |
VDOP |
PDOP |
X (м) |
Y (м) |
δ (м) |
|
1 |
4 |
4,1 |
1,0 |
4,22 |
432,9 |
79,92 |
214,05 |
|
2 |
4 |
4,2 |
1,0 |
4,32 |
119,88 |
166,5 |
120,06 |
|
3 |
5 |
9,5 |
4,9 |
10,69 |
0 |
113,22 |
220,18 |
|
4 |
5 |
3,3 |
1,0 |
3,45 |
179,82 |
133,2 |
52,01 |
|
5 |
6 |
3,0 |
1,0 |
3,16 |
179,82 |
66,6 |
52,01 |
Статистическое исследование одномерных выборок
1. Количество спутников. В пакете Statgraphics Centurion 15.2.11.0 вычислено среднее значение (Average), среднее квадратическое отклонение СКО (Standard deviation), асимметрия (Stnd. skewness), эксцесс (Stnd. kurtosis) и др. Некоторые результаты показаны в табл. 2 (для остальных выборок таблицы не приводим).
Таблица 2
Суммарная статистика по числу спутников
|
Count |
91 |
|
Average |
5,93407 |
|
Standard deviation |
1,50408 |
|
Minimum |
3,0 |
|
Maximum |
9,0 |
|
Range |
6,0 |
Минимальное значение – 3, максимальное – 9. Среднее число спутников в решении 5,9 при СКО, равном 1,5. Гипотеза о нормальности распределения не подтвердилась.
2. Горизонтальный геометрический показатель потери точности HDOP.
Минимальное значение – 1,0, максимальное – 14,7. Среднее значение 3,4 при СКО равном 2,4. В интервале радиуса 2,4 с центром в точке 3,4 находится 93 % значений (меньших 6), за пределами этого интервала находится 6 «плохих» значений параметра HDOP. Заметим, что обычно значение HDOP находится между 1 и 2 ([4]).
В нашем случае 70 % значений больше 2 и среднее значение равно 3,4. Поэтому в горизонтальной плоскости нужно ожидать значительную потерю точности. Гипотеза о нормальном распределении не подтвердилась.
3. Вертикальный геометрический показатель потери точности VDOP.
Минимальное значение – 0,8, максимальное – 8,4. Среднее значение 1,9 при СКО, равном 1,5. Три значения больше 6, т.е. примерно 97 % – относительно хорошие показатели. Обычно потеря точности в вертикальной плоскости больше, чем в горизонтальной, т.е. VDOP больше HDOP. Но в нашем эксперименте в среднем VDOP<HDOP. Гипотеза о нормальном распределении не подтвердилась.
4. Геометрический показатель потери точности PDOP.
Минимальное значение – 1,28, максимальное – 14,73. Среднее значение 4,21 при СКО, равном 2,6, 15 значений больше 6, т.е. примерно 84 % – хорошие показатели. Однако на открытой местности показатели PDOP меньше 6 в 95 % наблюдений ([4]). Гипотеза о нормальном распределении не подтвердилась.
5. Отклонение δ. Минимальное значение отклонения составило 0 м, максимальное – 590 м. Среднее значение примерно 70 м при СКО 92,4 м. За пределами интервала радиуса 92,4 с центром 70 находится 10 значений.
Статистическое исследование двумерных выборок
Прежде всего вычислим традиционные показатели корреляции изучаемых признаков, хотя, как уже показано, в силу недостоверности гипотезы о нормальном распределении признаков, линейная регрессионная модель здесь не достаточно точна.
1. Зависимость количества спутников и PDOP. В рамках линейной модели коэффициент корреляции –0,25. Корреляция между числом спутников и значением PDOP статистически значима с доверительной вероятностью 95 %.
2. Зависимость количества спутников и отклонения δ. В рамках линейной модели коэффициент корреляции –0,38. Корреляция между числом спутников и значением отклонения статистически значима с доверительной вероятностью 95 %.
3. Зависимость PDOP и отклонения δ. При доверительной вероятности 95 % нет статистически значимой зависимости между отклонением и значением PDOP.
Поскольку полученные данные не могут быть достаточно достоверными, исследуем зависимость PDOP и отклонения δ другим способом. Сгруппируем значения PDOP по качеству. Используем стандартные критерии из табл. 3.
После обработки сгруппированных по значению PDOP данных отклонения δ получена табл. 4.
Таблица 3
Стандартные качественные критерии PDOP
|
Качество PDOP |
Отличное |
Хорошее |
Среднее |
Ниже среднего |
|
значение PDOP |
меньше чем 3 |
от 3 до 6 |
от 6 до 8 |
больше чем 8 |
Таблица 4
Статистика δ по стандартным качественным критериям PDOP
|
Частота |
Среднее |
СКО |
Минимум |
Максимум |
|
|
PDOP отл. |
34 |
50,5403 |
43,1282 |
0,0 |
194,171 |
|
PDOP хор. |
43 |
66,6126 |
90,7846 |
0,0 |
587,969 |
|
PDOP cред. |
7 |
179,145 |
196,876 |
14,89 |
529,836 |
|
PDOP ниже сред. |
7 |
78,1068 |
73,823 |
19,98 |
220,183 |
|
Общие данные |
91 |
70,1481 |
92,4971 |
0,0 |
587,969 |
Для PDOP меньше 6 отклонение обычно не превосходит 100 метров ([4]). Но среди полученных данных для хороших (меньше 6) показателей PDOP есть даже максимальное отклонение 59 м. Применим другой способ группировки данных по значению PDOP.
Сгруппируем значения δ по новым критериям и сведем полученные результаты в табл. 6.
Таблица 5
Способы группировки по качеству PDOP
|
Качество PDOP |
Отличное |
Хорошее |
Среднее |
Ниже среднего |
|
Стандартное |
меньше чем 3 |
от 3 до 6 |
от 6 до 8 |
больше чем 8 |
|
Измененное |
меньше чем 2 |
от 2 до 4 |
от 4 до 6 |
больше чем 6 |
Таблица 6
Статистика δ по новым качественным критериям PDOP
|
Частота |
Среднее |
СКО |
Минимум |
Максимум |
|
|
PDOP отл. |
8 |
39,5914 |
18,1587 |
19,98 |
62,83 |
|
PDOP хор. |
49 |
52,4564 |
39,9235 |
0,0 |
194,171 |
|
PDOP сред. |
19 |
87,3473 |
135,75 |
0,0 |
587,969 |
|
PDOP ниже сред. |
15 |
128,626 |
152,162 |
14,89 |
529,836 |
|
Общие данные |
91 |
70,6877 |
93,9429 |
0,0 |
587,969 |
Таким образом, если PDOP меньше 4, то отклонение не больше 200 м и только ограничение PDOP меньше 2 приводит к точности порядка 70 м. При этом наблюдается также увеличение групповых средних наряду с увеличением групповых СКО. Подтверждается статистически значимое различие между группами.
Заключение
- Принимая критерий ([4]) «доступны как минимум четыре спутника», можно констатировать, что в 91 % наблюдений доступность была обеспечена.
- Число спутников и PDOP связаны слабой корреляционной зависимостью (отрицательный коэффициент корреляции –0,25), что означает в данном конкретном случае слабое влияние увеличения числа спутников в решении на уменьшение PDOP.
- Точность измерений, задаваемая величиной СКО ошибки, имеет порядок 100–200 метров по сравнению с не более чем 100 м на открытой местности ([4]), что объясняется затененностью антенны приемника.
- Более существенную роль для точности определения местоположения играют геометрические факторы расположения – HDOP и VDOP, количество спутников (если их три и более) существенной роли в данном случае не играет.
Таким образом, исследуя параметры спутниковой группировки, влияющие на точность определения местоположения приемника в условиях ограниченной видимости и многолучевости, можно рекомендовать повысить требования к геометрическим показателям точности для спутников, участвующих в решении. В этом случае повышаются статистические показатели точности до приемлемых, что косвенно свидетельствует о некоторой компенсации ошибки измерений, порождаемой переотражением.
Рецензенты:
Иванов В.Е., д.т.н., профессор, зав. кафедрой «Технологии и средства связи» ИРИТ-РТФ, Уральский федеральный университет им. Б.Н. Ельцина, г. Екатеринбург;
Леликова Е.Ф., д.ф.-м.н., профессор, ведущий научный сотрудник Института математики и механики им. Н.Н. Красовского, Уральское отделение Российской академии наук, г. Екатеринбург.
Работа поступила в редакцию 05.08.2014.
Библиографическая ссылка
Голикова Е.А., Малыгин И.В. ИССЛЕДОВАНИЕ СТАТИСТИЧЕСКИМИ МЕТОДАМИ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ АБОНЕНТА В УСЛОВИЯХ ОГРАНИЧЕННОЙ ВИДИМОСТИ КОСМИЧЕСКОГО СЕГМЕНТА GPS-ГЛОНАСС АНТЕННОЙ ПРИЕМНИКА // Фундаментальные исследования. – 2014. – № 9-7. – С. 1500-1504;URL: https://fundamental-research.ru/ru/article/view?id=35091 (дата обращения: 20.04.2024).



