При переработке высоковязких и пластичных материалов в электромагнитных механоактиваторах (ЭММА) [1, 2, 3, 4, 5] и смесителях [6, 7] наиболее предпочтительной является цилиндрическая форма ферромагнитных размольных тел [1, 3, 8]. Система намагниченных стержней, представляющих магнитоожиженный слой рабочего объема ЭММА, испытывает силовое и энергетическое воздействие со стороны деформированного магнитного поля [9, 10]. В актах энергонапряженных и регулируемых силовых контактов размольные тела целенаправленно передают энергию частицам перерабатываемого продукта, измельчая его статическим сжатием и ударом [10, 11, 12, 13]. Физико-математическая модель рабочего процесса формирования диспергирующего усилия [10, 14] включает результаты решения двух задач: определение деформированного магнитного поля и определение сил и моментов, действующих на стержень со стороны поля. Деформированное магнитное поле в рабочем объеме ЭММА описано системой интегральных уравнений с вырожденными ядрами [9]. В результате решения системы найдены неизвестные плотности простых слоев σi(φ), i = 1, …, n и определен потенциал Az(P) для любой точки Р плоскости, перпендикулярной осям стержней [9]. В статье представлены результаты решения второй задачи физико-математической модели рабочего процесса формирования диспергирующего усилия – задачи определения сил и моментов, действующих на стержень со стороны деформированного магнитного поля в рабочем объеме ЭММА.
Целью данной работы является решение задачи определения сил и моментов, действующих со стороны деформированного магнитного поля на систему размольных ферротел цилиндрической формы в рабочем объеме ЭММА.
Материал и методы исследований
Предметом исследований является рабочий процесс формирования силовых контактов в магнитоожиженном слое ферротел ЭММА.
Результаты исследований и их обсуждение
В результате решения первой задачи физико-математической модели формирования диспергирующего усилия в слое ферромагнитных размольных элементов (РЭ) определено деформированное магнитное поле и найдены неизвестные плотности простых слоев σi(φ), i = 1, …, n [9]. Таким образом, определен потенциал Az(P) для любой точки Р плоскости, перпендикулярной осям РЭ. Потенциальная энергия взаимодействия k-го токового слоя с суммарным магнитным полем остальных k – 1 РЭ и невозмущенного поля определена формулой
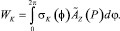 (1)
(1)
Условные обозначения и иллюстративный материал к решению первой и второй задач аналогичны и приведены в работе [9]. Точка Р принадлежит контуру сечения k-го РЭ. Потенциал Az(P) зависит только от обобщенных координат системы РЭ. Система из n РЭ, оси которых параллельны, определяется 3n обобщенными координатами. Такими обобщенными координатами могут служить, например, полярные координаты остальных (n – 1) РЭ относительно центра сечения k-го РЭ, как полюса и угла поворота каждого РЭ относительно собственной оси. Очевидно, что ввиду симметрии РЭ их поворот не влияет на магнитное поле. Поэтому потенциальная энергия поля не будет зависеть от этих углов. Следовательно, будут равны нулю моменты сил поворота РЭ относительно их осей. Рассмотрим выражение
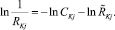
Разложим функцию 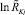 в ряд по степеням EKj:
в ряд по степеням EKj:
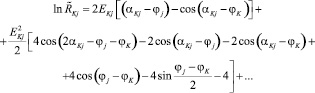 (2)
(2)
Интерес для рассматриваемой задачи представляют только третий, шестой и седьмой члены справа в формуле (2) [9]. Поэтому искомые аппроксимированные ядра имеют следующий вид:
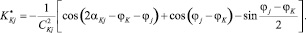 (3)
(3)
Таким образом, искомая потенциальная энергия взаимодействия k-го РЭ с внешним магнитным полем может быть представлена выражением
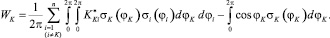 (4)
(4)
Силы и моменты, действующие на k-й РЭ со стороны внешнего для него магнитного поля, определены равенствами
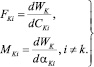 (5)
(5)
Распределение деформированных силовых линий магнитного поля при внесении в него однородного размольного элемента цилиндрической формы представлено на рис. 1, а. В этом случае из системы получаем
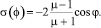 (6)
(6)
Потенциальная энергия сил взаимодействия РЭ с магнитным полем постоянна и не зависит от положения РЭ (WK = const). Поэтому главный вектор сил и главный вектор моментов, приложенных к одиночному РЭ в плоском магнитном поле, равны нулю. Этот вывод является очевидным, так как картина деформации магнитного поля симметрична относительно оси РЭ. При контактном взаимодействии двух РЭ цилиндрической формы в рабочем объеме ЭММА система интегральных уравнений имеет вид
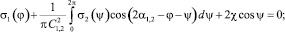
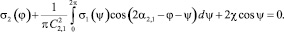 (7)
(7)
Поскольку С1,2 = С2,1 и ?1,2 = ?2,1 + ?, то ?1 = ?2 = ? и оба уравнения сводятся к одному
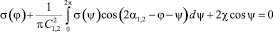 . (8)
. (8)
Решение интегрального уравнения имеет вид
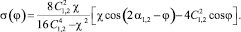 (9)
(9)
Картина эквипотенциальных линий (силовых линий) магнитного поля двух РЭ при С1,2 = 2 и α1,2 = 0, π/4, π/2 приведена на рис. 1, б, в, г. Потенциальная энергия взаимодействия первого РЭ с полем совпадает с потенциальной энергией взаимодействия второго РЭ с полем. Вычисленная с точностью до 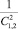 , эта энергия имеет вид
, эта энергия имеет вид
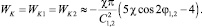 (10)
(10)
Потенциальная энергия в этом случае зависит только от двух обобщенных координат С1,2 и φ1,2. Момент сил МК, приложенных к системе, определен соотношением
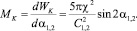 (11)
(11)
Поэтому если угол 0 < α1,2 < π/2, то возникает момент, который стремится увеличить этот угол, т.е. повернуть РЭ так, чтобы линия, соединяющая центры их сечений, расположилась параллельно силовым линиям невозмущенного поля.
Сила, действующая на первый РЭ, приложена к центру его сечения и направлена вдоль линии, соединяющей их центры сечений
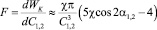 . (12)
. (12)
При α1,2 = 0, т.е. когда прямая линия, соединяющая центры сечений РЭ, перпендикулярна силовым линиям невозмущенного поля, имеем
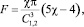 (13)
(13)
т.е. при достаточно большой магнитной проницаемости РЭ (μ >> 1) сила взаимодействия F > 0. Таким образом, в этом случае РЭ отталкиваются. При α1,2 = π/2 имеем
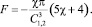 (14)
(14)
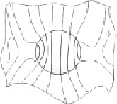 а
а 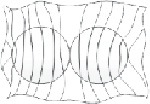 б
б 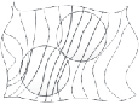 в
в
 г
г 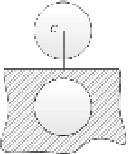 д
д
Рис. 1. К расчету силового взаимодействия между размольными элементами цилиндрической формы: а – ферромагнитный РЭ в магнитном поле рабочего объема; б – взаимодействие РЭ при С1,2 = 2 и α1,2 = 0; в – взаимодействие ферромагнитных РЭ при С1,2 = 2 и α1,2 = π; г – взаимодействие ферромагнитных РЭ при С1,2 = 2 и α1,2 = π/2; д – РЭ в магнитном поле около проводящей стенки
В этом случае F всегда отрицательна, т.е. РЭ притягиваются друг к другу.
Рассмотрим поведение одного РЭ в плоском магнитном поле около проводящей стенки (рис. 1, д). Этот случай легко сводится к предыдущему (если добавить второй РЭ, симметричный первому относительно стенки). При этом всегда существует сила притяжения РЭ к стенке рабочей камеры ЭММА, которая определяется по формуле
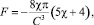 (15)
(15)
где С – расстояние от центра сечения РЭ до стенки рабочей камеры ЭММА.
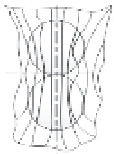
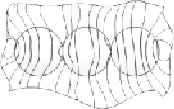
Картина эквипотенциальных линий магнитного поля трех ферромагнитных РЭ, помещенных в рабочий объем ЭММА, в случае, когда α = 0 и α = π/4, приведена на рис. 2, а, б. Аналогичное распределение линий получено при n-м количестве РЭ.
 а
а 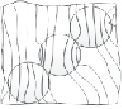 б
б
Рис. 2. Распределение эквипотенциальных линий магнитного поля в рабочем объеме ЭММА: а – структурная группа из РЭ в рабочем объеме ЭММА при α1,2,3 = 0; б – структурная группа из РЭ в рабочем объеме ЭММА при α1,2,3 = π/4
Заключение
В результате исследований определена величина сил и моментов, действующих на ферромагнитные размольные элементы со стороны деформированного магнитного поля в рабочем объеме ЭММА при различных коэффициентах его объемного заполнения ферромагнитной составляющей. На основании анализа физико-математической модели проведено обоснование рабочего процесса формирования диспергирующего усилия в магнитоожиженном слое ферротел ЭММА.
Рецензенты:
Ракутько С.А., д.т.н., заведующий лабораторией энергоэффективных электротехнологий ГНУ СЗ НИИМЭСХ, г. Санкт-Петербург;
Новоселов А.Г., д.т.н., профессор кафедры «Процессы и аппараты пищевых производств» Института холода и биотехнологий, Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики, г. Санкт-Петербург.
Работа поступила в редакцию 10.10.2014.
Библиографическая ссылка
Беззубцева М.М., Волков В.С., Обухов К.Н., Котов А.В. ОПРЕДЕЛЕНИЕ СИЛ И МОМЕНТОВ, ДЕЙСТВУЮЩИХ НА СИСТЕМУ ФЕРРОМАГНИТНЫХ РАЗМОЛЬНЫХ ЭЛЕМЕНТОВ ЦИЛИНДРИЧЕСКОЙ ФОРМЫ В МАГНИТООЖИЖЕННОМ СЛОЕ РАБОЧЕГО ОБЪЕМА ЭЛЕКТРОМАГНИТНЫХ МЕХАНОАКТИВАТОРОВ // Фундаментальные исследования. – 2014. – № 11-3. – С. 504-508;URL: https://fundamental-research.ru/ru/article/view?id=35550 (дата обращения: 19.04.2024).



