Большое применение, как в сельскохозяйственной технике, так и в других отраслях народного хозяйства находят устройства с вращающимися в кожухах и желобах спирально-винтовыми рабочими органами. Основным преимуществом подобных рабочих органов является их
дешевизна.
На основе теоретических и экспериментальных исследований разработаны и испытаны спирально-винтовые насосные устройства для перекачки жидких и полужидких сельскохозяйственных материалов. Для выкачки жидкостей из фляг, бочек жидкость захватывается витками пружины и по кожуху перемещается к сливному патрубку.
Для случаев выкачки жидкости из молочных фляг, бочек могут быть использованы: двигатель на 0,2 кВт, кожух полиэтиленовый (нержавеющие материалы) диаметром 38 мм, проволока диаметром 3...4 мм, частота вращения 1500 мин-1. При этом ведро в 10 л наполняется за время не более 1 минуты. Высота подъема 1...5 м. При высоте более 10 м (Н >g) частоту вращения спирального винта следует увеличивать до 2000...3000 мин-1. Проволочный винт средним радиусом r вращается с угловой скоростью щ и движется вдоль трубы с линейной скоростью ![]() Диаметр проволоки спирали обозначим д, ход винта - s, плотность жидкости - с, ее кинематическая вязкость -з.
Диаметр проволоки спирали обозначим д, ход винта - s, плотность жидкости - с, ее кинематическая вязкость -з.
Сила, действующая на жидкость со стороны одного витка проволочного винта, равна лобовому сопротивлению обтекающего его потока и вызывается разностью давлений по обе стороны потока и напряжениями трения: ![]() , где
, где ![]() - коэффициент лобового сопротивления, F - площадь проекции витка на плоскость поперечную движению,
- коэффициент лобового сопротивления, F - площадь проекции витка на плоскость поперечную движению, ![]() - относительная скорость набегающего потока. Перепад давления по потоку, обтекающего виток проволоки, определяется по формуле:
- относительная скорость набегающего потока. Перепад давления по потоку, обтекающего виток проволоки, определяется по формуле: ![]() , в которую подставляется скорость смеси
, в которую подставляется скорость смеси ![]() , и коэффициент сопротивления о.
, и коэффициент сопротивления о.
В случае подъема жидкости и движения проволочного винта в канале скорость перемещения жидкости относительно пружины ![]() где u - линейная осевая скорость движения проволочного винта, а н - осевая скорость жидкости относительно канала. Запишем уравнение Бернулли данного движения для объема, соответствующего шагу s винта вдоль оси z ,
где u - линейная осевая скорость движения проволочного винта, а н - осевая скорость жидкости относительно канала. Запишем уравнение Бернулли данного движения для объема, соответствующего шагу s винта вдоль оси z ,
![]() (1)
(1)
где hw- потери напора в трубопроводе на данном участке.
Принимая во внимание, что шаг винта пружины равен -20...60 мм, то на такой длине потери напора в уравнении (4) можно не учитывать. Тогда, подставив значение перепада давления из-за движения пружины из формулы:
![]() , (2)
, (2)
в уравнение (4), получим уравнение для определения осевой скорости жидкости
![]() (3)
(3)
Приведем его к виду, удобному для решения, и получим квадратное уравнение относительно н:
![]() . (4)
. (4)
Дискриминант этого уравнения равен: ![]() . При
. При ![]() , величина дискриминанта всегда положительна D>0, а при
, величина дискриминанта всегда положительна D>0, а при ![]() дискриминант положителен D>0 только при
дискриминант положителен D>0 только при ![]() . В этом случае линейная скорость движения должна удовлетворять неравенству:
. В этом случае линейная скорость движения должна удовлетворять неравенству: ![]() .
.
Далее, решая это квадратное уравнение (4), получаем значение скорости движения жидкости по трубопроводу:
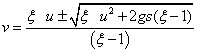 , при
, при ![]() . (5)
. (5)
Знак выбирается из физических условий, чтобы скорость движения была положительной.
В случае, когда коэффициент сопротивления ![]() из уравнения (4) следует решение:
из уравнения (4) следует решение: ![]() . Критическая скорость
. Критическая скорость ![]() при н = 0.
при н = 0.
Экспериментами установлено, что подача (производительность) барды влажностью 90,16 %, плотностью r = 1050 кг/м3, температуры 20°С пружинным насосом d = S = 35 мм, d = 4 мм, высоты подъема Н = 1,3 м, Dк = 45 мм составляет W = 450 кг/ч, N = 0,1 кВт. При этом осевая скорость пружины u = s n/30 =0,795 м/с, осевая скорость движения материала v = H/t = 1,3/4 = 0,324 м/с. При этом, коэффициент осевого отставания материала kv.= v / u = 0,324/0,795 = 0,408. Зависимость производительности W и N от частоты вращения пружины n.
Анализ таблицы показывает, что наименьший удельный расход энергии наблюдается при n =1900...2300 мин-1, коэффициент осевого отставания материала находится в пределах 0,3...0,4, производительность увеличивается пропорционально частоте вращения пружины.
Для сравнения полученной теоретической зависимости н по формуле (5) с результатами экспериментальных исследований проведен расчет скорости н(u). Для цилиндрической трубы с внутренним диаметром D = 38 мм, диаметром пружины dn=35 мм и диаметром проволоки д =4 мм коэффициент о равен 1,4. Подставив его значение в формулу (5), получим зависимость н(u).
Исследования показали, что для жидкости с плотностью с =1050 кг/м3 вязкостью ![]() м2/с совпадение результатов эксперимента с теоретической зависимостью н(u) наблюдается на большем участке эксперимента. Полученная теоретическая зависимость (5) позволяет, к тому же по значению критической частоты вращения (скорости пружины), при которой начинается подъем жидкости, определить истинное значение коэффициента о. Коэффициент осевого отставания материала
м2/с совпадение результатов эксперимента с теоретической зависимостью н(u) наблюдается на большем участке эксперимента. Полученная теоретическая зависимость (5) позволяет, к тому же по значению критической частоты вращения (скорости пружины), при которой начинается подъем жидкости, определить истинное значение коэффициента о. Коэффициент осевого отставания материала ![]() можно определить из формулы (5)
можно определить из формулы (5)
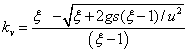 , и при
, и при ![]() ;
; 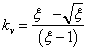 ,
,
что совпадает с результатами эксперимента и подтверждает механизм движения жидкости в сложных условиях вращения пружинного винта в канале и позволяет использовать полученные в работе данные при разработке и конструировании насосов и устройств, для транспортирования различных жидкостей.
Библиографическая ссылка
Исаев Ю.М. ОПРЕДЕЛЕНИЕ ОСЕВОЙ СКОРОСТИ ТРАНСПОРТИРОВКИ ЖИДКОСТЕЙ ИЗ ЕМКОСТЕЙ // Фундаментальные исследования. – 2008. – № 8. – С. 54-56;URL: https://fundamental-research.ru/ru/article/view?id=3571 (дата обращения: 24.04.2024).



