Наземные газотурбинные установки (ГТУ), которые создаются на базе авиационных двигателей, находят широкое применение для привода электрогенераторов на электростанциях малой и средней мощности [5]. Полученные на основе экспериментальных данных математической модели таких ГТУ имеют важное значение для совершенствования систем автоматического управления (САУ) ГТУ. Математические модели ГТУ находят разнообразное применение: они служат для испытания САУ на полунатурных стендах, для повышения надежности САУ, для настройки и оптимизации САУ, для диагностики, для формирования алгоритмов адаптивного управления. Поэтому исследование возможностей структурно-параметрической идентификации при создании многофункциональных моделей электроэнергетических ГТУ является сегодня актуальной задачей.
Опубликованные в статье результаты получены в рамках выполнения государственного задания Минобрнауки России № 13.832.2014/K.
Описание алгоритма структурно-параметрической идентификации
Задача структурной идентификации решается выбором системы нелинейных уравнений, наилучшим образом описывающих экспериментальные данные. В дальнейшем рассматриваются нелинейности вида произведения переменных. Перед тем как оценивать адекватность системы уравнений, для каждой из них должна быть решена задача параметрической идентификации. При этом решение задачи параметрической идентификации модели ГТУ ранее рассмотрено в работе [2]. Выбор структуры отдельного уравнения системы производится варьированием количества задействованных переменных линейной части уравнения, количеством слагаемых нелинейной части уравнения и составом перемножаемых переменных:
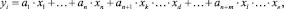 (1)
(1)
где i – номер уравнения в системе; a1, an, an+m – коэффициенты уравнения; n – количество переменных, задействованных в идентификации (для модели ГТУ в упрощенном случае это: расход топлива; частота вращения турбокомпрессора; частота вращения свободной турбины; мощность нагрузки); m – количество коэффициентов нелинейной части уравнения; k, d, l, e – некоторые перемножаемые переменные нелинейной части уравнения.
При этом нелинейное уравнение можно формально представить в виде линейного путем замены произведений переменных нелинейной части некоторыми условными переменными:
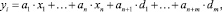 (2)
(2)
где d – произведение переменных x.
После такого преобразования на уравнение (2) можно распространить алгоритм параметрической идентификации [2].
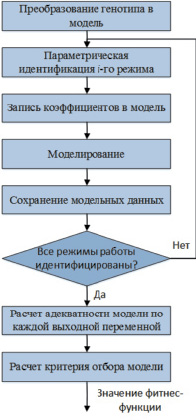
Рис. 1. Алгоритм расчета фитнес-функции
Таким образом, решение задачи структурной идентификации представляет собой оптимизационную задачу, в которой критерием является отклонение модельных данных от экспериментальных, например, по методу наименьших квадратов. Данную задачу сложно представить для решения специализированными методами поиска локального и глобального минимума. Предварительные исследования показали, что наиболее просто она решается посредством генетического алгоритма.
При этом фитнес-функция генетического алгоритма изображена блок-схемой алгоритма на рис. 1.
Критерий отбора модели на основе адекватности модели включает все выходные переменные модели:
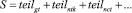 (3)
(3)
где S – критерий отбора модели; teilgt, teilntk, teilnct – меры адекватности модели по переменным расхода топлива, частоты вращения турбокомпрессора и свободной турбины соответственно, рассчитанные по методу Тейла [4].
Кроме того, критерий отбора включает ограничения на каждую меру адекватности. При выходе за ограничения мера адекватности умножается на повышающий коэффициент, который растет с дальнейшим увеличением меры адекватности. Начальное значение повышающего коэффициента равно количеству мер адекватностей, включенных в критерий.
Генотип и соответствующий ему фенотип для уравнений с нелинейностями в виде умножения нескольких переменных представляется в следующем виде.
Реализация алгоритма
При тестировании собственных алгоритмов исследователи прибегают к реализации их на одном из языков программирования. Большое значение для достижения результата при этом имеет качество программного кода, включая архитектуру. В первую очередь неаккуратная архитектура или её отсутствие может сильно затруднить и ограничить разработчика в решении задачи. Кроме того, значение качества кода растет при увеличении команды разработчиков. К критериям оценки качества кода относятся: структурированность; читабельность; краткость; сопровождаемость; надежность; эффективность; безопасность; тестируемость и другие. При низком качестве кода в течение разработки программы количество ошибок в ней растет, скорость и мотивация дальнейшей разработки падает. В своей книге [3] Роберт Мартин демонстрирует график этой зависимости и методы увеличения качества кода программного обеспечения.
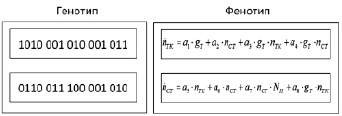
Рис. 2. Генотип и фенотип при решении задачи структурной идентификации модели ГТУ генетическим алгоритмом (gТ – расход топлива, nТК – частота вращения турбокомпрессора, nСТ – частота вращения свободной турбины, NН –мощность нагрузки, a1…a8 – коэффициенты)
Алгоритм был реализован на языке программирования Java. На рис. 3 представлена упрощенная диаграмма классов UML структурной идентификации. Использование интерфейсов позволяет абстрагироваться от реализаций и предоставляет гибкость их замены. А разбитие программы на классы и модули и минимальная связность между ними увеличивает читабельность и простоту отладки.
Моделирование и генетический алгоритм реализуются независимыми модулями без привязки к частной задаче. Модуль параметрической идентификации адаптирован под модель, приводимую к линейному виду (2). Структурная же идентификация модели интегрируется в генетический алгоритм посредством реализации классов фитнес функции (Fitness Model Calculator) и создателя хромосомы (Equation Chromosome Creator). Equation Chromosome Creator необходим для задания ограничений на хромосомы в конкретной решаемой задаче.
В реализации калькулятора фитнес-функции (класс Fitness Model Calculator)присутствует обращение к блокам параметрической идентификации модели и моделирования. Для исключения повторения операции моделирования при дублировании генотипов используется кэш значений фитнес-функций по уникальному хэш-коду генотипа:
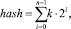 (4)
(4)
где n – суммарное количество генов в генотипе; i – индекс гена генотипа; k – значение гена (единица или ноль).
При нехватке размера типа Long для хранения хэш-кода в Java может быть использован тип Big Decimal. Помимо этого использование параллельных вычислений ускоряет выполнение алгоритма.
Результаты экспериментов
Ранее была получена структура линейной модели в ходе проведения большого количества экспериментов, на что потребовалось затратить значительное количество времени. При использовании же автоматической структурно-параметрической идентификации посредством генетического алгоритма поиск нелинейной модели сократился до нескольких минут, помимо этого меры адекватности улучшились.
Структура нелинейной модели ГТУ для газотурбинной электростанции (ГТЭС), полученная в ходе работы генетического алгоритма в виде двух уравнений.
Уравнение частоты вращения турбокомпрессора:
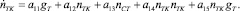 (5)
(5)
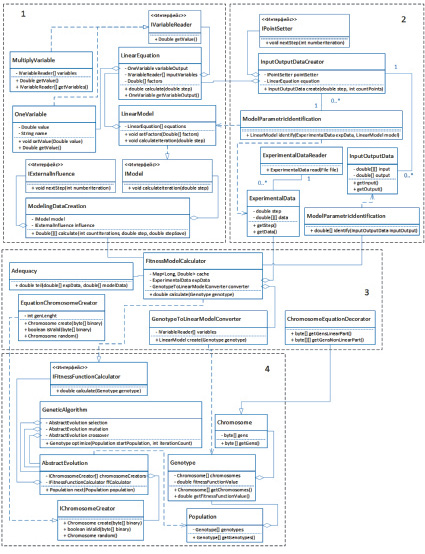
Рис. 3. Упрощенная UML диаграмма классов модуля структурной идентификации: 1 – модуль моделирования; 2 – модуль параметрической идентификации; 3 – структурно-параметрическая идентификация модели; 4 – модуль генетического алгоритма
Уравнение частоты вращения свободной турбины:
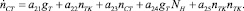 (6)
(6)
где gT – расход топлива; nТК – частота вращения ротора турбокомпрессора; nСТ – частота вращения ротора свободной турбины; NН – нагрузка на валу.
Коэффициенты aij непрерывно изменяются с помощью интерполяции по таблице в зависимости от режима работы ГТУ. Таблица таких коэффициентов предварительно формируется в результате параметрической идентификации для нескольких выбранных режимов работы ГТЭС.
На рис. 4 отображено сравнение экспериментальных и модельных данных для режима сброса нагрузки.
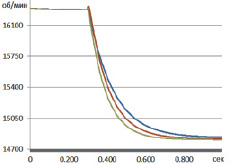
Рис. 4. Графики частоты вращения свободной турбины (оранжевая – экспериментальная, голубая – модельная линейной модели, розовая – модельная нелинейной модели)
Полученная модель ГТУ показала лучшую адекватность по сравнению с исходной линейной по методу Тейла [5]. Для линейной модели значение меры адекватности составило 0,0041, а для нелинейной – 0,002.
Выводы
Полученная в результате работы генетического алгоритма нелинейная математическая модель ГТУ может обеспечивать лучшую адекватность по сравнению с линейной моделью для выбранных режимов работы. Она может быть использована в составе перспективных адаптивных САУ. Разработанное программное обеспечение позволяет строить математические модели и проводить моделирование не только для газотурбинных установок, но может быть адаптировано и под другие объекты. В свою очередь реализация генетического алгоритма легко адаптируется под различные оптимизационные задачи.
Рецензенты:
Бочкарев С.В., д.т.н., доцент кафедры «Микропроцессорные средства автоматизации», Пермский национальный исследовательский политехнический университет, г. Пермь;
Цаплин А.И., д.т.н., профессор, заведующий кафедрой «Общая физика» Пермский национальный исследовательский политехнический университет, г. Пермь.
Работа поступила в редакцию 06.11.2014.
Библиографическая ссылка
Килин Г.А., Один К.А., Кавалеров Б.В. СТРУКТУРНО-ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ МОДЕЛИ ГАЗОТУРБИННОЙ УСТАНОВКИ НА ОСНОВЕ ГЕНЕТИЧЕСКОГО АЛГОРИТМА // Фундаментальные исследования. – 2014. – № 11-7. – С. 1480-1484;URL: https://fundamental-research.ru/ru/article/view?id=35791 (дата обращения: 25.04.2024).



