Составление прогнозов развития производства продукции представляет собой актуальную задачу на местном, региональном, федеральном уровнях, для отдельных организаций. В силу ряда микро- и макроэкономических причин на современном этапе экономических реформ сделать это довольно трудно. В настоящее время не существует общепризнанных методов, которые позволяют прогнозировать развитие производства продукции в организациях на перспективу с удовлетворительной достоверностью. Также необходимо отметить, что укрепление экономической свободы участников воспроизводственного процесса на уровне регионов обуславливает вероятностный образ экономических процессов, происходящих в различных отраслях, и заставляет применять сценарный подход и многовариантные альтернативные пути поиска решений.
Для решения данной проблемы предлагается использовать методы экономико-математического моделирования и многомерного статистического анализа – один из главных инструментов прогрессирования хозяйственного механизма, структурного преобразования регионального рынка и прогнозирования динамики производства и реализации продукции. Изменения, происходящие в современной экономике, приводят к составлению новых и совершенствованию разработанных систем экономико-математического моделирования. Все это позволяет выявить скрытые резервы экономического роста организаций на уровне региона.
Разновидностью экономико-математических моделей является оптимизационная модель. Ее использование позволяет подвергнуть анализу динамику развития организаций региона и воспользоваться большими массивами реальной информации.
В данной статье предлагается построенная на ряде ограничений (что соответствует определенному использованию производственных ресурсов) модель оптимизации производства сельскохозяйственной продукции, которая позволит предприятию повысить рентабельность своего производства [1].
В настоящий момент финансово-экономическое состояние сельскохозяйственных организаций различных формообразований остается достаточно сложным. Отрицательное воздействие на финансово-экономическое состояние сельскохозяйственных организаций оказывают следующие факторы:
– увеличение физического и морального износа основных производственных фондов;
– снижение урожайности сельскохозяйственных культур как печальное следствие уменьшения минеральных удобрений из-за отсутствия денег;
– падение объемов производства сельскохозяйственной организации и сбыта ее различных видов продукции;
– низкие объемы инвестиций в инфраструктуру производственного и социального назначения;
– недостаточная обеспеченность специалистами и отсутствие квалификации задействованных производственных рабочих;
– снижение технической оснащенности сельхозтоваропроизводителей [9].
Итоговая цель создания модели заключается в формировании эффективных предпосылок интенсивного развития сельскохозяйственного производства и получения наибольшей прибыли, что является важным показателем эффективности финансово-экономической деятельности. Это обеспечивается рациональным использованием возможных производственных ресурсов и способствует повышению рентабельности хозяйственной деятельности сельскохозяйственных организаций в современных условиях. [8].
Решение разработанной экономико-математической модели проводится в несколько этапов (рисунок).
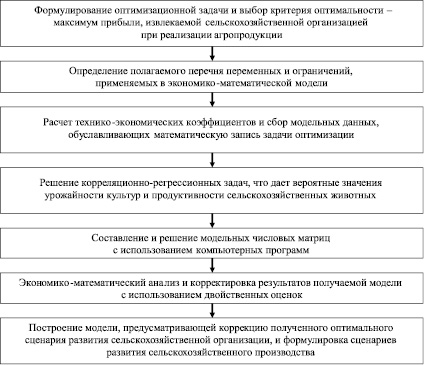
Этапы разработки экономико-математической модели по оптимизации производства продукции
Предполагается деление входной информации на следующие группы:
1. Производственные расходы (трудовые, на образование страхового фонда, на корма, на материальные затраты в расчете на единицу произведенной сельскохозяйственной продукции).
2. Результаты переменных (данные урожайности сельскохозяйственных культур и продуктивности животных – уровни выхода товарной и валовой продукции, кормовых единиц и протеина).
3. Земельные ресурсы, объемы в соответствии с производством, использованием и реализацией сельскохозяйственной продукции.
Разработанные модели оптимизации позволяют свести до возможного минимума недостаток ресурсов, имеющийся в сельскохозяйственных организациях, главным образом за счет рационального использования трудовых, земельных, финансовых, технических и других n-ресурсов, удобрений и кормов. Поставленная задача достигается через критерий оптимизации анализируемой системы [10].
Максимум прибыли, получаемый благодаря реализации сельскохозяйственной продукции, выступает критерием оптимизации. Он является целевой функцией. Данное предпочтение обосновывается тем, что прибыль является одним из значимых показателей финансово-экономической эффективности деятельности сельскохозяйственных организаций. Это позволяет обеспечить оптимальное применение имеющихся производственных n-ресурсов и повысить рентабельность сельскохозяйственной организации в современных условиях. Выделенный критерий оптимизации – максимум прибыли на полный планируемый срок перспективного развития сельскохозяйственных организаций – в соответствии со своим содержанием вполне соответствует решению данной оптимизационной задачи.
Исследование модели на множества появляющихся в процессе решения других вариантов развития сельскохозяйственного производства позволяет изучить и обнаружить наилучший вариант в соответствии с согласованным критерием оптимизации. Отобранный критерий, согласно установленной задаче, отвечает требованию обеспечения выполнения обязательств по поставкам продукции в соответствии с договорами и в государственные фонды. Тем самым учитывается круг интересов и заказчика продукции, и ее производителей [3].
При построении оптимизационной модели необходимо учитывать следующие основные переменные: поголовье скота по видам, площади кормовых угодий, посевные площади сельскохозяйственных культур. Помимо основных, в модели включаются и вспомогательные переменные, которые отражают величины производства и реализации продаваемой продукции растениеводческой и животноводческой отраслей, оптимальную организацию рационов корма животных, объемы производства и расходования кормов [5].
В модель также вводятся ограничения:
– гарантированное производство основных видов товарной продукции для государственных фондов и обязательное выполнение в соответствии с договорами о поставках сельскохозяйственной продукции;
– величина земельных ресурсов, поголовья скота;
– производство и использование кормов;
– производство и реализация сельскохозяйственной продукции;
– финансовые ресурсы.
В рамках существующих границ региона исследования применяются изменения базовых параметров составленных моделей, которые в свою очередь опираются на фактические размеры отраслей растениеводства и животноводства.
В моделях число неизвестных и ограничений определяется в процессе подготовки матрицы, которая учитывает конкретные особенности хозяйств. При определении переменных необходимо также учитывать производственное применение получаемой организациями региона сельскохозяйственной продукции, содержание сельскохозяйственных животных и агротехнические и зоотехнические особенности возделывания отдельных культур [7].
Использование многофакторного анализа корреляционно-регрессионного типа для расчета порядка модельных коэффициентов осуществляется по нескольким производственным функциям с целью выбора наилучших прогнозируемых вероятных уровней показателей всходов сельскохозяйственных культур и продуктивности животных с экстраполяцией данных динамических рядов.
Рассчитывается предлагаемый оптимальный баланс в экономико-математических моделях производства и потребления кормов. Моделирование кормовой базы предполагает, что для каждого вида сельскохозяйственных животных корма должны быть агрегированы в соответствии с группой детализации отдельных видов кормов [4].
Составленные экономико-математические модели являются статически значимыми. Оптимизационную задачу структуры сельскохозяйственного производства для каждой организации региона можно представить следующим образом:
Z = X – Y → max,
где Z – целевая функция, выраженная в максимизации прибыли; X – совокупность выручки от реализации сельскохозяйственной продукции; Y – совокупность производственных затрат на продукцию.
На основе составления модели решаемой задачи при экономико-математическом моделировании предполагается использование методов математической формализации условий и требований, предъявляемых к производству сельскохозяйственной продукции.
При решении задачи и выбора наилучшего варианта развития и размещения производства необходимо использовать систему ограничений сельскохозяйственной продукции, которая включает пределы снизу и сверху. Это позволит обеспечить достижение планируемых темпов прироста при правильной организации сельскохозяйственной продукции не только по количественным, но и качественным техническим и экономическим показателям [6].
Построение оптимизационной задачи включает следующие ограничения:
1. По использованию кормовых угодий и пашни:
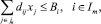
где j – порядковый номер переменной (j = 1, 2, …, n); i – порядковый номер ограничений (i = 1, 2, …, m); dij – затраты i-го n-ресурса на единицу измерения j-й отрасли; xj – аргумент, обозначающий размер j-й отрасли; Вi – ограничивающий размер угодий сельскохозяйственного назначения i-го вида; Jn – множество переменных в соответствии с сельскохозяйственными культурами и угодьями; Im – множество ограничений в соответствии с использованием пашни и кормовых угодий.
2. По соотношению посевных площадей и сельскохозяйственных культур:
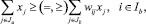
где wij – компонента пропорциональности между отдельными сельскохозяйственными культурами; Ja – множество переменных в соответствии с использованием сельскохозяйственных культур в севооборотах; Ib – множество ограничений в соответствии с севооборотными требованиями.
3. По группам кормов:
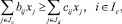
где bij – выход i-го вида кормовых единиц в расчете для единицы измерения j-й растениеводческой отрасли; cij – необходимость i-го вида одной головы j-го вида скота в группе кормов; Jc – множество переменных в соответствии с кормопроизводством; Jd – множество переменных в соответствии с животноводческой отраслью; Ic – множество ограничений в соответствии с кормовым балансом.
4. По производству и использованию сельскохозяйственной продукции:
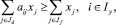
где aij – выход продукции i-го вида в расчете для единицы измерения j-й отрасли; Jd – множество переменных в соответствии с видами отраслей животноводства; Jf – множество переменных в соответствии с видами реализуемой продукции; Iy – множество ограничений в соответствии с производством и с использованием продукции.
5. По гарантированному объему производства сельскохозяйственной продукции:
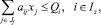
где Qi – гарантируемый объем производства продукции; Iz – множество ограничений в соответствии с гарантированным производством продукции.
6. По определению совокупной выручки:
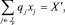
где qj – выход товарной продукции в денежном выражении для единицы j-й отрасли; Jp – множество переменных в соответствии с суммированием выручки от реализации продукции.
6. По определению производственных затрат:
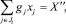
где gj – затраты материальных средств в денежном выражении для единицы j-й отрасли; Jt – множество переменных в соответствии с суммированием себестоимости сельскохозяйственной продукции.
7. Критерий неотрицательности переменных:
xj ≥ 0.
Любое накладываемое ограничение соответствует использованию производственных ресурсов, что в свою очередь позволяет обеспечить балансовую увязку количества n-ресурсов с их наличием в сельскохозяйственной организации.
Степень развития производственного, n-ресурсного потенциалов для каждой сельскохозяйственной организации определяется совокупностью переменных. Единицами измерения переменных в модели являются не только натуральные показатели (гектары, центнеры), но и стоимостные показатели.
Также при построении оптимизационных моделей необходимо учитывать, что все функционирующие в административных границах сельскохозяйственные организации имеют заданные почвенно-климатические условия и, соответственно, для них должны быть определены равные экономические обстоятельства. Также нужно обратить внимание на то, что при построении для отдельной сельскохозяйственной организации моделей производства присущи альтернативность развития при одинаковом начальном объеме вовлеченных ресурсов.
В итоге решения оптимизационной задачи предполагается полный учет и колебаний урожайности культур, и продуктивности животных, и всех производных от экономических показателей (производительности труда, себестоимости и цены реализации производимой продукции).
Для ориентации на максимально возможный уровень эффективности при определении перспектив развития сельскохозяйственных организаций необходимо учитывать реальные результаты и задействованные производственные n-ресурсы. Следовательно, имеется неодинаковость в модельных вариантах, что предполагает внесение коррекции уровней урожайности культур и продуктивности сельскохозяйственных животных, денежных расходов и цен реализации сельскохозяйственной продукции с учетом официального уровня инфляции [1].
Также в итоге получаемые оптимизационные модели позволяют обнаружить наиболее оптимальные величины производства различных видов сельскохозяйственной продукции и их комбинацию между собой. Для каждой сельскохозяйственной организации в процессе проведения расчетов определяются:
– размеры и состав отраслей сельскохозяйственного производства и их рациональное соответствие в общем количестве;
– распределение с учетом требований севооборота основных сельскохозяйственных культур;
– поголовье скота, обеспеченного полноценными кормами и помещениями содержания, объемы кормового производства и его использования, оптимальные рационы в кормлении животных;
– величины производства продукции отраслей растениеводства и животноводства и ее реализации;
– основные результативные показатели финансово-экономической деятельности [2].
Установление двойственных оценок для производства сельскохозяйственной продукции и для использования производственных ресурсов сопровождается решением главной задачи.
Таким образом, построение моделей, предложенных в исследовании, позволяет выявить вариант, оптимальный для сочетания структур сельскохозяйственного производства, и на этой базе размеры объемов производства продукции для сельскохозяйственных организаций в перспективе. Исполнение рассчитанных оптимальных вариантов на практике, как следствие, приведет к стабильному увеличению прибыли, обеспечению рентабельной работой сельскохозяйственных товаропроизводителей, которую можно направить на расширение и развитие производства и на удовлетворение социальных потребностей.
Практическое осуществление составленных моделей, в соответствии с предварительными оценками, позволит уменьшить расходы на производство сельскохозяйственной продукции и, соответственно, улучшить финансовый результат как показатель успешного ведения аграрными организациями хозяйственно-производственной деятельности.
Также применение результатов моделирования поможет выделить те приоритетные перспективы деятельности сельскохозяйственных организаций, которые следует развивать с учетом имеющихся климатических условий, культурных и национальных традиций сельского населения и его производственной квалификации.
Рецензенты:
Коледин С.В., д.э.н., профессор, заведующий кафедрой «Экономика АПК», филиал, Уральский государственный экономический университет, г. Челябинск;
Пряхин Г.Б., д.э.н., профессор кафедры «Экономика и управление», ФГБОУ ВПО «Уральский государственный университет физической культуры», г. Челябинск.
Работа поступила в редакцию 12.11.2014.
Библиографическая ссылка
Лысенко М.В., Лысенко Ю.В., Таипова Э.Х. ЭКОНОМИКО-МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОПТИМИЗАЦИИ ПРОИЗВОДСТВА ПРОДУКЦИИ // Фундаментальные исследования. – 2014. – № 11-8. – С. 1750-1755;URL: https://fundamental-research.ru/ru/article/view?id=35841 (дата обращения: 20.04.2024).



