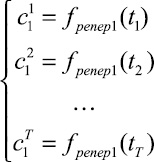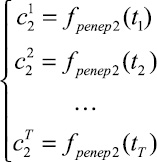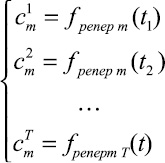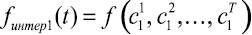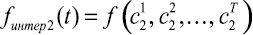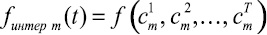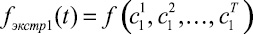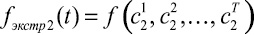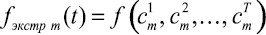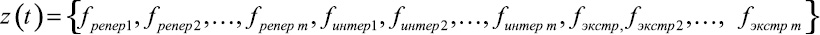Математический аппарат классического прогнозирования строится на аппроксимации исследуемого параметра с последующим экстраполированием на указанный срок прогноза. Такой подход ориентирован на обработку только числовых последовательностей, в то время как экспертные суждения, которыми зачастую вынуждены пользоваться составители прогнозов, выражены в большинстве своем в виде объектов нечисловой природы. В настоящее время методика получения статических числовых весов альтернатив на основе анализа матриц вербальных парных сравнений активно популяризируется Т.Л. Саати [1]. В русскоязычной литературе большое внимание подобным методикам уделено в работах автора [2–4], А.В. и О.Н. Андрейчиковых [4, 5] и др.
Согласно рекомендациям [1] эксперт выносит n(n – 1)/2 суждений и формирует квадратную обратносимметричную матрицу  , содержащую парные сравнения множества из n элементов (альтернатив), где n – порядок матрицы, равный числу сравниваемых элементов, а v1, v2, ..., vn – соответственно их веса (интенсивности). При использовании метода анализа иерархий для прогнозирования необходимо найти аналитическое решение задачи о динамическом (изменяющемся на периоде прогнозирования суждений о приоритетности) собственном значении матрицы
, содержащую парные сравнения множества из n элементов (альтернатив), где n – порядок матрицы, равный числу сравниваемых элементов, а v1, v2, ..., vn – соответственно их веса (интенсивности). При использовании метода анализа иерархий для прогнозирования необходимо найти аналитическое решение задачи о динамическом (изменяющемся на периоде прогнозирования суждений о приоритетности) собственном значении матрицы  [1, 8, 10] парных сравнений:
[1, 8, 10] парных сравнений:
A(t)⋅w(t) = lmax(t)⋅w(t),
где A(t) – матрица  , содержащая тенденции изменения суждений о весах v1, v2, ..., vn; w(t) – динамический собственный вектор квадратной обратносимметричной матрицы; lmax(t) – динамическое собственное число матрицы A(t).
, содержащая тенденции изменения суждений о весах v1, v2, ..., vn; w(t) – динамический собственный вектор квадратной обратносимметричной матрицы; lmax(t) – динамическое собственное число матрицы A(t).
Если известна тенденция изменения суждения, то можно предпринять попытку построения зависимости, описывающей эти изменения. Согласно теории Галуа [17] наибольший порядок матрицы, для которой с помощью простой квадратуры можно получить lmax в явной форме, равен четырем. В работе «Разработка средств прогнозирования технических решений на основе иерархических моделей» предложен и реализован [3], а в работах [4, 8, 10] развит метод анализа числовых рядов, элементами которых являются функциональные зависимости, отражающие динамические экспертные суждения.
Метод включает:
1. Численный (не алгебраический) анализ динамических матриц парных сравнений, содержащих функциональные зависимости, прогнозирующие динамику приоритетов.
2. Формирование многомерной матрицы, содержащей t срезов состояния исследуемой иерархической системы предпочтений на каждый из t моментов времени интервала прогнозирования (матрица содержит множество статических МПС, соответствующих им локальных и глобальных векторов приоритетов).
3. Интерполяцию многомерной мат рицы по каждому альтернативному направлению (метод интерполяции подбирается экспертом в зависимости от решае мой задачи).
4. Экстраполяцию состояний иерархической системы с формированием аналитического (функционально-параметрического) описания прогнозируемых трендов.
Графически метод представлен на рис. 1, где верхний и нижний индексы 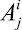 обозначают, что j-ю альтернативу оценивали по i-му критерию, r – количество альтернатив, p – количество критериев. Индексы элемента вектора приоритетов
обозначают, что j-ю альтернативу оценивали по i-му критерию, r – количество альтернатив, p – количество критериев. Индексы элемента вектора приоритетов 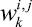 показывают, что w есть вес j-й альтернативы по i-му критерию в k-й момент времени, где k = 1, ..., T, а T – количество моментов времени. При исследовании поведения системы на больших промежутках времени мощность множества w(t) позволяет проводить регрессионный анализ.
показывают, что w есть вес j-й альтернативы по i-му критерию в k-й момент времени, где k = 1, ..., T, а T – количество моментов времени. При исследовании поведения системы на больших промежутках времени мощность множества w(t) позволяет проводить регрессионный анализ.

Рис. 1. Численный метод прогнозирования динамики приоритетов
Таким образом, каждая динамическая оценка 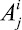 (элемент анализируемого множества) сама является множеством реперных точек, по которым предстоит построить функциональную зависимость. Каждая реперная точка представляет собой оценку интенсивности проявления исследуемой характеристики в данный момент времени, то есть статическую экспертную оценку. Учитывать динамику экспертных предпочтений предлагается путем получения срезов состояния системы в определенные моменты времени, интерполяции данных и построении на их основе экстраполирующих зависимостей (рис. 2). Интерполяция применяется для построения гладких кривых на интервале времени, ограниченном крайними реперными точками, множество которых задает эксперт при парной оценке альтернатив. Экстраполяция применяется для построения отрезков кривых на интервале прогнозирования, но за пределами, ограниченными крайними реперными точками.
(элемент анализируемого множества) сама является множеством реперных точек, по которым предстоит построить функциональную зависимость. Каждая реперная точка представляет собой оценку интенсивности проявления исследуемой характеристики в данный момент времени, то есть статическую экспертную оценку. Учитывать динамику экспертных предпочтений предлагается путем получения срезов состояния системы в определенные моменты времени, интерполяции данных и построении на их основе экстраполирующих зависимостей (рис. 2). Интерполяция применяется для построения гладких кривых на интервале времени, ограниченном крайними реперными точками, множество которых задает эксперт при парной оценке альтернатив. Экстраполяция применяется для построения отрезков кривых на интервале прогнозирования, но за пределами, ограниченными крайними реперными точками.
|
Динамическое множество = {m элементов в виде множества реперных точек} для описания функций от времени на интервале от t1 до T |
|||||||||
|
Множество реперов: |
{fрепер1 (t)} |
{fрепер2(t)} |
… |
{fрепер m(t)} |
|||||
|
Статические значения (константы) функции fi(t) на каждый момент времени из интервала T |
|||||||||
|
zn: |
|
|
… |
|
|||||
|
Интерполяция множества констант ci на интервале, ограниченном реперами |
|||||||||
|
zi: |
|
|
... |
|
|||||
|
Экстраполяция множества констант ci на интервале прогнозирования T |
|||||||||
|
ze: |
|
|
… |
|
|||||
|
Функционально-аналитическое представление исследуемого числового множества |
|||||||||
|
|
|||||||||
Рис. 2. Анализ числовых множеств, элементами которых являются функциональные зависимости, отражающие динамические экспертные оценки. Обозначения: z(t) – динамика состояний исследуемой системы; zn – срез состояния системы на моменты времени, на которые достоверно известны числовые значения показателей; zi – срез состояния системы на моменты времени, на которые возможно построить интерполяционные зависимости между достоверно известными числовыми значениями показателей; ze – срез состояния системы на моменты времени, на которые возможно построить экстраполяционные зависимости по построенным ранее интерполяционным; fрепер i – множество реперных точек, описывающих i-е изменение предпочтений; сi j – i-я реперная точка в j-й момент времени; fинтер i – i-я интерполяционная зависимость, ограниченная реперными точками; f экстр i – i-я экстраполяционная зависимость, на интервале прогнозирования, но за пределами, ограниченными крайними реперными точками
Автоматизация численного анализа динамических матриц парных сравнений заключается в формировании кортежа статических матриц. Каждая статическая матрица в кортеже представляет собой следующий временной срез на указанном в динамической матрице интервале прогнозирования. Ориентированный граф алгоритма численного анализа приведен на рис. 3. Нумерация узлов графа соответствует нижеприведенному списку:
1 – чтение из базы данных сведений об иерархической структуре показателей;
2 – выбор исследуемого узла в иерархической структуре;
3 – выбор и чтение из базы данных динамической матрицы, содержащей описание функциональных зависимостей в каждой из ячеек матрицы;
4 – определение временного интервала прогнозирования;
5 – установка текущего момента времени t;
6 – выбор очередной ячейки в динамической матрице;
7 – если ячейка содержит функциональную зависимость, то переход к узлу 11;
8 – если ячейка содержит числовую константу, то в статическую матрицу записывается эта константа (переход к узлу 14);
9 – если ячейка пуста или содержит маркер автоматического заполнения матрицы, переход к узлу 10;
10 – алгоритм автоматического заполнения матрицы по содержащейся в ней избыточной информации;
11 – поиск в базе данных вида функции и списка её параметров;
12 – подстановка параметра t в функцию и расчет значения функции;
13 – формирование очередной ячейки статической матрицы на момент времени t;
14 – формирование очередной статической матрицы на момент времени t в кортеже матриц (или создание кортежа);
15 – расчет множества векторов приоритетов для каждой из сформированных статических матриц в кортеже – формирование кортежа, элементами которого являются векторы приоритетов альтернатив на каждый из моментов времени;
16 – запись кортежа векторов приоритетов в базу данных;
17 – аппроксимация динамики приоритетов для динамической матрицы;
18 – субъективный визуальный анализ полученных трендов;
19 – изменение динамических оценок путем аппроксимации реперных точек на плоскости предпочтений;
20 – изменение динамических оценок на плоскости предпочтений путем подбора параметров функций;
21 – редактирование или формирование новой динамической матрицы парных сравнений;
22 – запись динамической матрицы парных сравнений в базу данных.
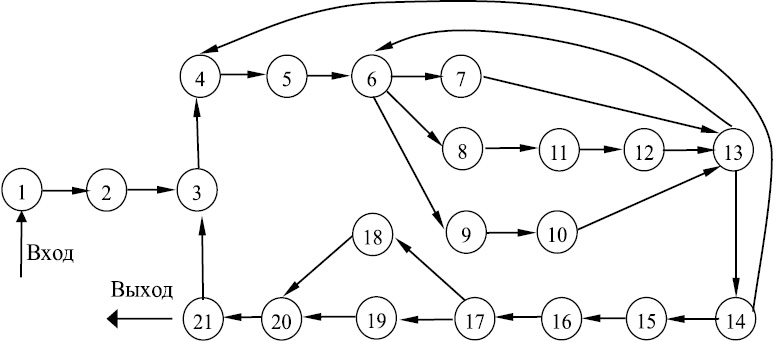
Рис. 3. Граф алгоритма автоматизации численного анализа динамических матриц парных сравнений
При заполнении матриц парных сравнений в ряде случаев возникает проблема несогласованности суждений. Чаще всего это происходит из-за того, что эксперт не достаточно точно оценивает альтернативы в рамках предоставленной шкалы. Когда эксперт заполняет МПС с динамикой предпочтений, то ошибки несогласованности могут накапливаться с течением времени, что приводит к неверным результатам. Кроме того, функциональное описание трендов, представленное в [1], не всегда точно удовлетворяет субъективным представлениям экспертов об изменении предпочтений альтернатив по тому или иному критерию со временем. И, наконец, возможна ситуация, когда эксперт просто не может предоставить данные по изменению каких-либо отдельных парных сравнений в матрице. Для преодоления этих проблем можно порекомендовать разработанный автором в [3] и реализованный в [7] алгоритм заполнения некоторых ячеек матрицы парных сравнений по уже содержащейся в ней информации.
Практика показывает, что часто эксперты не могут дать конкретного значения для парного сравнения элементов системы на какой-то определенный момент в будущем. Более логичным было бы задание некоторого интервала предпочтений для каждого момента времени t, то есть в данный момент предпочтение может принять значение от «сильное превосходство» (число 5) до «значительное превосходство» (число 7) в шкале [1]. При подобном подходе мы получаем две кривых f1 и f2, которые ограничивают область изменения предпочтений на интервале времени, для которого составляется прогноз (рис. 4).
Как должны производиться расчеты в данном случае? В работах автора [8, 10] предлагается применение следующего алгоритма:
1. Для каждой точки оси абсцисс на заданном интервале времени эксперты указывают два значения предпочтительности одной альтернативы по сравнению с другой (f1 и f2 на рис. 4, а).
2. Для каждого момента времени автоматически формируются две матрицы парных сравнений.
3. Рассчитываются векторы локальных приоритетов на основе анализа двух матриц.
4. Для всей системы оценок производится свертка и рассчитываются два вектора глобальных приоритетов.
5. Каждый вектор сохраняется в соответствующей таблице с указанием момента времени, для которого производится расчет.
6. Шаги 1–4 повторяются для всего прогнозируемого интервала.
7. Полученные таблицы обрабатываются любым из известных методов интерполяции для получения результирующих кривых (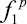 и
и 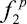 на рис. 4, б), ограничивающих доверительный интервал прогнозирования приоритетности для данной альтернативы.
на рис. 4, б), ограничивающих доверительный интервал прогнозирования приоритетности для данной альтернативы.
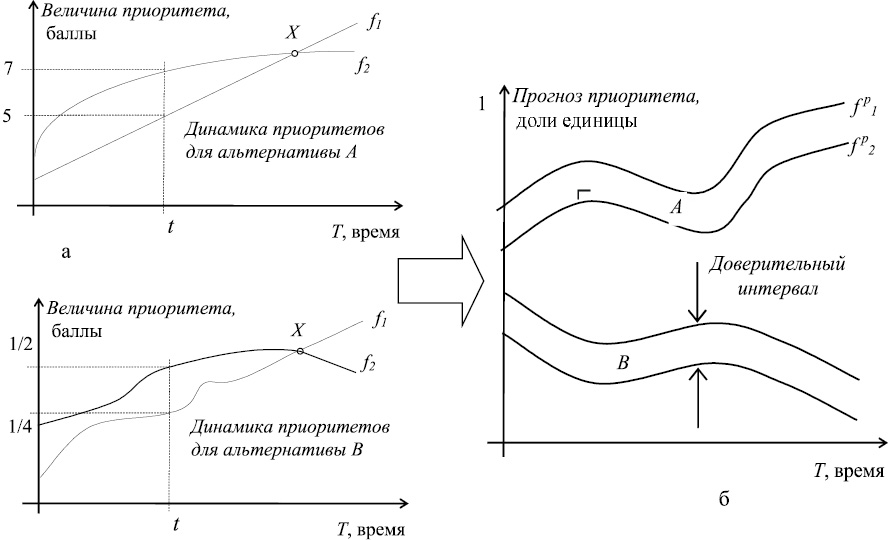
Рис. 4. Прогноз приоритетности на основе экспертных интервальных оценок на плоскости предпочтений
Результатом работы приведенного выше алгоритма будут две кривые, ограничивающие возможную область изменения предпочтения альтернатив относительно цели исследования (фокуса иерархии).
Для оценки удельной точности полученного прогноза можно порекомендовать следующую интегральную оценку Ie:
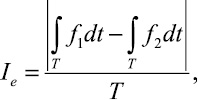
где Т – интервал времени, для которого составляется прогноз; f1 и f2 – функции, заданные экспертом.
При этом экстремальными значениями удельной точности для шкалы [1] будут числа, близкие к 9 и 0. Число примерно равное 9, получим, если эксперт в качестве возможного интервала укажет весь диапазон применяемой шкалы (числа от 1/9 до 9), что при составлении прогноза является совершенно недопустимым. Число, равное нулю, получим в совершенно противоположном случае, то есть если обе функции в прогнозируемом интервале совпали (например, как в точке Х на рис. 4). Методики и программные средства, позволяющие нивелировать эти проблемы, а также значительно расширяющие возможности исследователей при исследовании и прогнозировании динамики социо-экономических систем на основе многокритериального анализа динамических экспертных предпочтений подробно рассмотрены в работах автора [8–10].
Исследование выполнено при финансовой поддержке РГНФ в проекте проведения научных исследований «Динамическое нечеткое моделирование социально-экономических показателей региона», проект № 14-12-34010.
Рецензенты:Гущина Е.Г., д.э.н., доцент кафедры «Мировая экономика и экономическая теория», Волгоградский государственный технический университет, г. Волгоград;
Московцев А.Ф., д.э.н., профессор, заведующий кафедрой «Менеджмент, маркетинг и организация производства», Волгоградский государственный технический университет, г. Волгоград.
Работа поступила в редакцию 26.11.2014.