В ходе эксплуатации месторождений возникают аварийные ситуации, последствия которых могут быть катастрофическими как для конкретного месторождения, так и для гидроминеральной базы региона в целом [5]. Причиной подобных ситуаций является некорректный выбор режима добычи воды из скважины. Одним из способов решения проблемы является разработка распределенной системы управления, способной поддерживать стабильный режим добычи минеральной воды [4].
Важным этапом построения распределенной системы является математическое моделирование объекта управления. Математическая модель объекта позволяет, приложив к объекту управления воздействие необходимого типа и интенсивности, увидеть динамические изменения внутри месторождения. Это позволяет предотвратить такие процессы, как появление депрессионной воронки и разлом пласта [1].
В данной работе предлагается рассмотреть способы моделирования гидродинамических процессов на примере Георгиевского и Кисловодского месторождений минеральных вод региона Кавказские Минеральные Воды. Кавказские Минеральные Воды являются уникальным рекреационно-лечебным регионом, главным преимуществом которого является наличие минеральных вод различного химического состава. На территории в 546,5 тыс. га сосредоточено 24 месторождения минеральных вод (Кисловодское, Ессентукское, Нагутское и др.) с суммарными утверждёнными эксплуатационными запасами в 15600 м3/сут. Известно, что, несмотря на рост потребности в минеральной воде, реальный объем добычи в регионе составляет менее 30 % от возможного [7]. Одним из факторов, снижающих объем добычи, является сложное гидрогеологическое строение месторождений региона.
Постановка задачи
Для стабильной добычи гидроминеральных ресурсов необходимо использование методов математического моделирования. Математическая модель месторождения минеральных вод представляет собой систему дифференциальных уравнений, включающую уравнения геофильтрации и массопереноса. Решение данной системы уравнений делится на два этапа: определение скорости фильтрации и расходов потоков между центрами модельных блоков (задача геофильтрации) и определение изменения вещественного состава и количества находящегося в жидкости вещества (задача массопереноса) [3].
Для решения задачи геофильтрации составляется геофильтрационная модель, которая является плоскопространственным или объемным представлением объекта с заданными начальными и граничными условиями, учитывающим динамические характеристики пластовых процессов. Исходными данными для моделирования являются данные о количестве пластов и их емкостных параметрах, эксплуатационные данные и др.
Модель массопереноса (геомиграционная модель) – это замкнутая система дифференциальных уравнений процессов переноса мигрантов физико-химического обмена веществ и гидродинамических превращений с условиями однозначности для каждого процесса [1].
В работе рассматривается практика моделирования месторождений минеральных вод. В качестве примеров выбраны Кисловодское и Георгиевское месторождения. Данные о выбранных гидролитосферных объектах приведены в табл. 1.
Таблица 1
Таблица гидрогеологических параметров месторождений
|
Месторождение |
Скважины |
Тип воды |
Глубина залегания (м) |
Дебит |
Размеры |
|
Кисловодское |
7-РЭ, 2-Б-бис и д.р. 7, 5/0 8-бис, 23 и д.р. |
Нарзан, Доломитный нарзан, Сульфатный нарзан |
100–400 |
1500 |
20×20 |
|
Георгиевское |
3 Юг, 4 ЮГ, 1, 2, 3, 4, 5, 6 и др. |
Хлоридно-натриевые воды, йодо-бромистые |
1300–1600 |
2900 |
6,3×1,56×2,6 |
По данным приведенной таблицы можно увидеть, что месторождения сильно отличаются. Глубина залегания воды является одним из наиболее важных параметров, так как с увеличением глубины повышается внутрипластовое давление, что сильно влияет на протекание моделируемых процессов. Несмотря на различия в глубине и условий залегания, рассмотренный выше подход был успешно применен.
Методика расчета
В общем виде система исходных дифференциальных уравнений, описывающих пространственный процесс геофильтрации и массопереноса, может быть представлена в следующем виде:
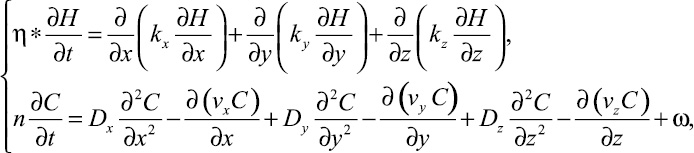 (1)
(1)
где η* – упругоемкость породы, 1/м; kx, ky, kz – коэффициенты фильтрации по соответствующим координатам, м/сут; H – функция напора; n – активная пористость; Dx, Dy, Dz – коэффициент динамической дисперсии; C – концентрация исследуемого компонента;
vx, vy, vz – компоненты скорости фильтрации; ω – параметр, характеризующий интенсивность внутрипластовых обменных процессов.
Систему уравнений (1) необходимо дополнить граничными и начальными условиями. Наряду с параметрическим обеспечением модели данные условия определяются в ходе гидрогеологических работ. Для решения системы уравнений используются численные методы. Дифференциальные уравнения преобразуются методом конечных разностей, что дает возможность представить уравнение в дискретной форме по координатам времени и пространства.
В некоторых случаях для упрощения модели используется только уравнение геофильтрации. Это вызвано сложностью верификации модели вследствие увеличения количества параметров при учете массопереноса. Тем не менее использование модели объекта, описанного только уравнением геофильтрации, дает качественные результаты. Пример подобного подхода к моделированию гидролитосферных объектов описан в трудах Малкова А.В. и Першина И.М. [3]. Объектом моделирования является Георгиевское месторождение минеральных вод. Математическая модель Георгиевского месторождения имеет следующий вид:
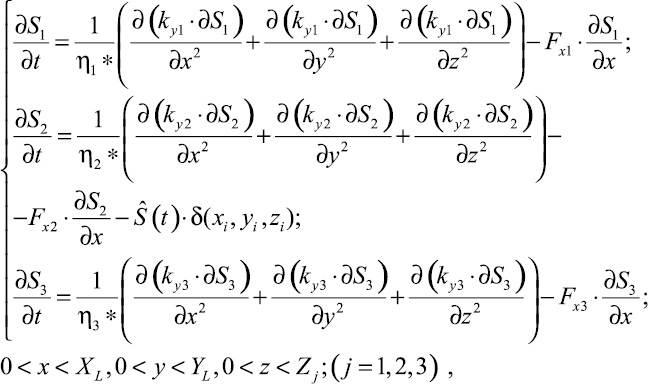 (2)
(2)
где j – номер пласта; Fx,j – скорость движения воды в j водоносном пласте; 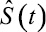 – управляющее воздействие.
– управляющее воздействие.
Физический смысл 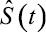 – управляющее воздействие на объект управления, приложенное в точках дискретизации. В этих точках δ(x, y, z) = 1. В остальных точках
– управляющее воздействие на объект управления, приложенное в точках дискретизации. В этих точках δ(x, y, z) = 1. В остальных точках
δ(x, y, z) = 0. 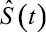 – это дебит (водозабор из скважин).
– это дебит (водозабор из скважин).
Начальные условия заданы как
Sj(x, y, z, 0) = 0. (3)
Граничные условия внутри объекта заданы как
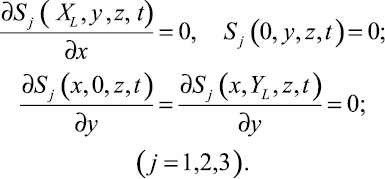 (4)
(4)
Граничные условия на границах пласта представлены как
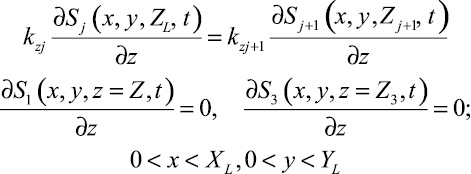 (5)
(5)
В данной модели взяты три пласта месторождения, поэтому она позволяет наиболее точно прогнозировать техногенные изменения в месторождении в целом.
Наиболее приближенный к реальным условиям подход к моделированию месторождений минеральных вод был использован на базе ОАО «Нарзан». В качестве объекта моделирования взято Кисловодское месторождение минеральных вод. Результаты моделирования изложены в трудах Малкова А.В. и Дубогрея В.Ф. [2]. Для описания пространственного процесса геофильтрации и массопереноса была предложена следующая математическая модель:
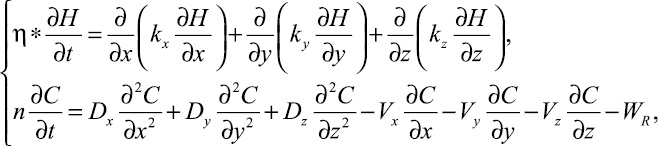 (6)
(6)
где Vx, Vy, Vz – компоненты скорости фильтрации; WR – параметр, характеризующий интенсивность внутрипластовых обменных процессов.
Данная модель позволяет параллельно учитывать фильтрационные и миграционные процессы, протекающие в месторождении минеральных вод, что позволяет более четко отразить реальное состояние объекта. Использование обоих уравнений значительно усложняет вычисления, но дает реальное представление о протекающих в месторождении процессах.
Обсуждение результатов
Математическое моделирование Георгиевского и Кисловодского месторождений минеральных вод дало качественные результаты. В первую очередь это обусловлено использованием реальных данных, полученных в ходе геологоразведочных и гидрогеологических работ. Параметрическое обеспечение моделей рассматриваемых месторождений представлено в табл. 2.
Таблица 2
Таблица параметров математических моделей месторождений
|
Месторождение |
Математическая модель |
Коэффициент |
Коэффициент |
|
Георгиевское |
ДУ (2) Начальные условия (3) Граничные условия (4,5) |
0,2 |
1,5∙10–7–2,25∙10–7 |
|
Кисловодское |
ДУ (6) |
0,2 |
2∙10–5 |
Результатом совместной работы гидрогеологов и специалистов-прикладников стала адекватная модель, отражающая процессы, протекающие в моделируемых месторождениях.
В общем случае существуют два подхода к разработке модели:
1. Составить сложную модель, учитывающую все возможные факторы, что влечет за собой трудность математических расчётов и реализации на ЭВМ.
2. Составить более простую математическую модель, которая должна отображать сущность происходящих процессов.
При оценке адекватности модели, как существующей, так и проектируемой, может быть использовано ограниченное подмножество различных состояний. В связи с этим для оценки достоверности полученных результатов моделирования большое значение имеет проблема устойчивости модели [6]. Как известно, вычислительные схемы могут быть образованы по разомкнутому и замкнутому циклам. В данном случае для вычислений используются схемы с замкнутым циклом, при использовании которых устойчивость модели зависит от физических параметров протекающих процессов. Используя методы ТАУ, можно выбрать параметры таким образом, чтобы вычислительная схема была устойчива.
Факт успешного апробирования разработанных моделей на добывающих предприятиях доказывает адекватность модели. В данном исследовании рассматривалась геофильтрационная модель Георгиевского месторождения и модель геофильтрации и массопереноса Кисловодского месторождения. Моделирование было произведено на основе данных гидрогеологических работ. Использование реальных данных о месторождениях и гидрогеологических процессах позволило провести успешную верификацию моделей, что качественно отразилось на результатах моделирования. Погрешность вычислений при моделировании Кисловодского месторождения составила 10–20 %. При моделировании Георгиевского месторождения использовалась трехмерная модель месторождения. Моделируемое месторождение представлено в виде объекта, состоящего из трех водоносных пластов, разделенных слабопроницаемыми пропластками. На всех участках водоносный горизонт напорный. Процесс водоотбора осуществляется из 5 водозаборных скважин, которым соответствуют 5 контрольных скважин. Коэффициенты упругоемкости были заданы отдельно для каждого пласта, в свою очередь коэффициент фильтрации был принят единым для всего месторождения. Общая квадратичная погрешность вычислений при использовании данной модели составила 14 %.
По приведенным данным видно, что результаты дают хорошую сходимость реальных и модельных данных. Проведенное исследование позволяет выработать унифицированный подход к построению геофильтрационных моделей. Полученные результаты могут быть использованы для синтеза распределенной системы управления гидролитосферными процессами каждого месторождения региона Кавказских Минеральных Вод.
Выводы
Проведен анализ геофильтрационных моделей Кисловодского и Георгиевского месторождений минеральных вод региона КМВ. Показано моделирование системы из нескольких водоносных пластов. В ходе исследования процесса выполняется уточнение параметров модели, что позволяет добиться устойчивости рассматриваемой схемы. Показано, что данный алгоритм может быть применен к рассмотренным моделям месторождений без ограничений. Рассмотренные модели являются достоверными, так как исследования проводились на базе разрабатывающих предприятий. Наличие большого объема данных геологоразведочных и гидрогеологических работ по месторождениям обеспечивает успешную апробацию алгоритма. Отмечено, что предлагаемый механизм анализа месторождений минеральных вод позволяет выявлять закономерности их функционирования и может служить предпосылкой к разработке универсальной системы управления месторождениями минеральных вод.
Рецензенты:Малков А.В., д.т.н., профессор, директор ОАО «Нарзан», г. Кисловодск;
Першин И.М., д.т.н., профессор, зав. кафедрой «Управление в технических и биомедицинских системах», Институт сервиса, туризма и дизайна (филиал), ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Пятигорск.
Работа поступила в редакцию 28.11.2014.
Библиографическая ссылка
Мартиросян А.В., Мартиросян К.В. АНАЛИЗ СПОСОБОВ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МЕСТОРОЖДЕНИЙ МИНЕРАЛЬНЫХ ВОД // Фундаментальные исследования. – 2014. – № 11-12. – С. 2599-2603;URL: https://fundamental-research.ru/ru/article/view?id=36029 (дата обращения: 25.04.2024).



