Лечение рецидивных и диссеминированных злокачественных новообразований (ЗНО) остается одной из сложнейших проблем онкологии [8, 10]. Прогноз для больного в этом случае, как правило, оценивается как неблагоприятный, и целью лечения становится не выздоровление больного, а максимальное продление ему жизни [4, 6]. При этом стоит отметить, что продолжительность жизни пациентов с распространенными ЗНО часто зависит не столько от проводимого лечения, сколько от скорости роста опухолевых очагов. По мнению ряда авторов, смерть организма неизбежно наступает при достижении опухолевыми очагами критических размеров, не совместимых с жизнедеятельностью организма [3]. В зависимости от кинетических особенностей опухолей период этот может продолжаться от нескольких недель до нескольких лет [7]. Целью данной работы мы поставили изучение скорости роста рецидивных и метастатических опухолей различных локализаций. Для достижения поставленной цели нами совместно с сотрудниками кафедры математики Нижегородского университета имени Н.И. Лобачевского разработана оригинальная пошаговая модель опухолевого роста. Длина одного шага нашей модели равна продолжительности клеточного цикла клеток опухоли. Существует достаточно большое количество математических моделей опухолевого роста [1, 2, 5, 9]. При построении нашей модели мы исходили из нескольких основных позиций:
1. Опухоль по своей структуре неоднородна. Она состоит из паренхимы и стромы. Кроме того (как правило, в центре опухоли) опухоль включает в себя зоны некрозов. У разных пациентов эти компоненты выражены в разных пропорциях.
2. Рост опухоли происходит за счет деления клеток паренхимы в процессе митоза.
3. Одновременно в опухоли идет процесс убыли клеток (так называемый фактор клеточных потерь (ФКП)) прежде всего за счет процессов некроза и апоптоза клеток. Известно, что в процессе роста раковой опухоли погибает (от некроза и апоптоза, без всякого лечебного воздействия 97–99 % всех раковых клеток [3]).
4. Скорость роста опухоли есть производное от соотношения процессов деления клеток и фактора клеточных потерь.
5. На скорость роста опухоли влияет также длительность клеточного цикла (промежуток времени от появления новой раковой клетки до ее гибели или следующего деления). За период этого цикла раковая клетка проходит три фазы: фазу подготовки к митозу (интерфазу), собственно фазу митоза и фазу пролиферативного покоя (рис. 1).
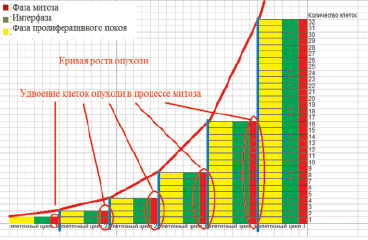
Рис. 1. Рост опухоли в результате деления клеток паренхимы при прохождении ими клеточного цикла
6. Теория больших чисел позволяет нам утверждать, что в опухоли в определенный момент времени соотношение количества клеток паренхимы в каждой из трех указанных фаз равно соотношению продолжительности каждой из этих фаз.
7. Таким образом, зная длительность одной из фаз клеточного цикла, а также долю клеток в разных фазах цикла, мы из этого пропорционального соотношения вычисляем длительность клеточного цикла. Наиболее постоянная величина в клеточном цикле опухолевой клетки – это длительность митоза. По данным ряда авторов в опухолях человека митоз длится около 1 часа [11].
Таким образом, чтобы построить кинетическую кривую роста рецидивной или метастатической опухоли для каждого конкретного пациента, нам необходимы следующие входные параметры для нашей модели:
- Период времени от предыдущей радикальной операции до выявления рецидивного или метастатического очага опухоли.
- Размер вторичного опухолевого очага. Его объем измеряется при помощи встроенных опций при ультразвуковом исследовании, либо компьютерной томографии. Исходя из соотношения, что в 1 см3 опухоли содержится около 109 клеток, определяем примерное количество клеток в опухоли (V).
- Структура опухоли определяется при ее морфологическом исследовании (в нашем исследовании бралось 7–10 биоптатов из разных участков опухоли). С использованием цитометрических методик определяются следующие параметры опухоли: доля паренхимы (n), доля стромы и доля некрозов в объеме опухоли. Нас интересует прежде всего количество клеток в паренхиме опухоли N = V∙n.
- В самой паренхиме определяем долю клеток в состоянии митоза (X), долю клеток в состоянии интерфазы (Y) (для определения у используем иммунногистохимические методики. Известно, что клетки в состоянии интерфазы экспрессируют антиген Ki67). Вычисляем долю клеток в состоянии пролиферативного покоя Z = 1 – X – Y.
- Соотношение, описанное в пунктах 6 и 7 можно описать уравнением:
X/tx = Y/ty = Z/tz.
- Зная значение длительности фазы митоза (tx), равное 1 часу, находим значения t (продолжительность клеточного цикла), ty (длительность интерфазы) и tz (длительность фазы пролиферативного покоя).. Продолжительность интерфазы и фазы клеточного покоя рассчитываются соответственно, как
ty = (Y∙tx)/X и tz = (Z∙tx)/X.
Таким образом, суммируя длительность всех трех фаз вычисляем продолжительность клеточного цикла:
t = tx + ty + tz.
- Изменение количества клеток паренхимы опухоли в промежутке времени, равном длительности клеточного цикла, можно описать уравнением
N1 = N0·X·(1 - b)·2 + N0·Y·(1 - с) + N0·Z(1 - d).
В этой формуле b – доля патологических нежизнеспособных митозов. с и d – доли опухолевых клеток, гибнущих в процессе интерфазы и фазы пролиферативного покоя.
- На следующем шаге построения нашей модели, через промежуток времени, равный уже двум клеточным циклам (2t) от начала отсчета (времени забора биопсийного материала), количество клеток в паренхиме опухоли будет описываться уравнением
N2 = N1·X·(1 - b)·2 + N1·Y·(1 - с) + N1·Z(1 - d).
Таким же методом можно вычислить N3, N4 и так далее. Соединяя точки (N1, N2, N3 и т.д.) на графике зависимости размера опухоли от времени, можно получить кривую роста опухоли.
- Можно провести вычисления в обратном порядке (определить N–1, N–2). Например:
N-1 = N0/(X·(1 - b)·2 + Y·(1 - c) + Z·(1 - d)).
Определить в ретроспективе характер роста опухоли от 1 раковой клетки до момента времени, когда проводится обследование больного.
На базе описанной выше математической модели для удобства вычислений нами с помощью сотрудников кафедры математики Нижегородского университета им.Н.И. Лобачевского создана компьютерная программа (использован язык программирования С++). Интерфейс программы изображен на рис. 2.
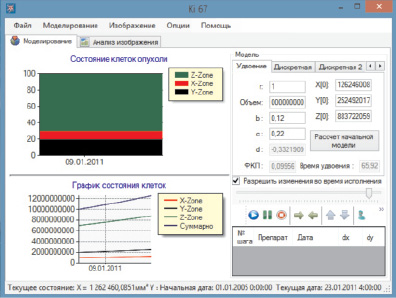
Рис. 2. Интерфейс программы моделирования опухолевого роста
Программа позволяет для каждого конкретного обследуемого по нашей методике пациента вычислить такие параметры, как скорость роста опухоли (учитывая экспоненциальный характер кривой роста, определяется время удвоения опухоли), ФКП, а также построить кривую роста опухоли. В левой половине интерактивного окна программы отображены график соотношения структурных элементов паренхимы (вверху) и кривая роста опухоли (внизу). В правой половине окна программы – форма, позволяющая задавать вводные параметры для расчета (вверху), а также панель управления программой (внизу).
Приведем следующие примеры, применения описанной программы в клинической практике.
Пациентка Е. 49 лет. В 2002 г. по поводу рака левой молочной железы 2А стадии в Нижегородском областном онкологическом диспансере прошла комбинированное лечение и 6 курсов химиотерапии. Через 8 лет в 2010 г. в области послеоперационного рубца заметила уплотнение 1 см диаметром. Других отдаленных метастазов не выявлено. Цитометрическое исследование удаленного рецидивного очага позволило определить структуру опухоли: строма составляла 37 % от объема опухолевого узла, доля клеток в состоянии митоза – 9,69 %, доля клеток в состоянии интерфазы – 9,18 %, доля клеток в состоянии пролиферативного покоя – 32 %, доля некрозов в объеме опухоли 12 %. Данные цитометрии, а также размер паренхимы опухоли были обработаны при помощи указанной выше компьютерной программы. Получены следующие параметры: время удвоения опухоли 110 суток, фактор клеточных потерь 99,85 %. Получен также график роста опухоли больной Е. Несмотря на высокую пролиферативную активность опухоли (доля клеток в состоянии митоза 9,69 %), скорость роста опухоли оценивается как медленная. Это явление обусловлено прежде всего высокими клеточными потерями (ФКП 99,85 %). Прослежена дальнейшая судьба этой больной. На конец 2014 г. она жива, перенесла еще две операции по иссечению рецидивных очагов из послеоперационного рубца, получает гормонотерапию.
Приведем пример более агрессивного течения опухолевого процесса. Больной П. 21 год. В июле 2009 г. перенес широкое иссечение меланомы кожи спины. В январе 2010 г. обратился в Нижегородский областной онкологический диспансер с метастатическим поражением паховых лимфатических узлов слева (размер очага 2 на 1 на 1 см). При цитометрии удаленного препарата выявлен следующий структурный состав опухоли: доля стромы 9 % от объема опухоли, доля клеток в состоянии митоза – 13,6 %, клеток в интерфазе – 51 %, клеток в состоянии пролиферативного покоя – 20 %, некрозы составляли 6 % от опухолевого узла. При обработке данных при помощи нашей программы получено: время удвоения опухоли – 6 суток, ФКП – 96,98 %. Высокая скорость роста в данном случае была обусловлена сочетанием высокой митотической активности опухоли (13,6 %) и умеренных клеточных потерь (ФКП 96,98 %). Прогноз оценивался как неблагоприятный. Больному еще дважды иссекались метастазы из подкожной клетчатки, проводилась химиотерапия. Продолжительность жизни больного П. составила 29 месяцев после нашего исследования.
Таким образом, разработанная модель опухолевого роста и компьютерная программа на основании данной модели позволяют определить такие важные прогностические параметры, как время удвоения опухоли и фактор клеточных потерь.
Рецензенты:
Базаев А.В., д.м.н., профессор, заведующий кафедрой общей хирургии, Нижегородская государственная медицинская академия, г. Нижний Новгород;
Меньков А.В. д.м.н., профессор, профессор кафедры общей хирургии, Нижегородская государственная медицинская академия, г. Нижний Новгород.
Работа поступила в редакцию 29.12.2014.
Библиографическая ссылка
Базанов К.В. МОДЕЛИРОВАНИЕ РОСТА РЕЦИДИВНЫХ И МЕТАСТАТИЧЕСКИХ ОПУХОЛЕЙ // Фундаментальные исследования. – 2014. – № 10-9. – С. 1685-1689;URL: https://fundamental-research.ru/ru/article/view?id=36492 (дата обращения: 23.04.2024).



