Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Алтухов В.И. 1 Касьяненко И.С. 1 Казаров Б.А. 2 Санкин А.В. 1 Филлипова С.В. 1

---

1 Филиал ФГАОУ ВПО «Северо-Кавказский федеральный университет»

2 Кавминводский институт (филиал) ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова»

Поскольку в одноосных совершенных «идеальных» кристаллах происходит подавление флуктуаций поляризации (кулоновскими дальнодействующими силами), то в них происходит расширение области применимости около Тк термодинамической теории Ландау-Гинзбурга. С другой стороны, в очень узком интервале температур вблизи Тк проявляются аномальное поведение и крайне резкие скачки тепловых характеристик кристаллов. В работе с единых позиций на основе микроскопической модели мягкой моды рассчитаны и дано объяснение аномальному около Тк поведению диэлектрической проницаемости теплоемкости и коэффициента теплового расширения совершенных кристаллов ТГС. Определены значения важных параметров теории: температурная зависимость мягкой моды, величина скачка теплоемкости около Тк, поведение теплоемкости в широком интервале температур и величина скачка коэффициента теплового расширения около Тк. Результаты расчетов согласуются с соответствующими экспериментами.

Статья в формате PDF

2253 KB

диэлектрическая проницаемость

теплоемкость вдоль оси 2

коэффициент теплового расширения

аномальное поведение

мягкая мода

фазовый переход

ТГС

1. Алтухов В.И. Основы теории кинетических свойств кристаллов с дефектами и фазовыми переходами: диэлектрики и сегнетоэлектрики. – Ставрополь: СевКавГТУ, 2003. – 190 с.

2. Алтухов В.И. Симметрия и структурные фазовые переходы в кристал­лах. – СевКавГТУ: Ставрополь, 2003. –96 с.

3. Алтухов В.И., Казаров Б.А., Касьяненко И.С., Санкин А.В., Филлипова С.В. Расчет аномального поведения коэффициентов теплопроводности и теплового расширения сегнетокерамики на основе твердых растворов цирконата-титаната свинца. Фундаментальные исследования. – ИД «Академия естествознания», 2014. – № 9, Ч. 5. – С. 1008–1013.

4. Алтухов В.И., Ростова А.Т., Казаров Б.А. Рассеяние фононов на точеч­ных дефектах структуры, комплексах-наночастицах и типичные осо­бенности теплового сопротивления реальных кристаллов и сегнетоэлектриков // Нано- и микросистемная техника. – 2006. – № 3. – С. 11–19.

5. Казаров Б.А., Алтухов В.И., Дядюк М.Н., Митюгова О.А. Модель температурного поведения теплового сопротивления сегнетоэлектрических кристаллов триглицинсульфата. Фундаментальные исследования. – ИД «Академия естествознания», 2014– № 9, Ч. 4. – С. 728–733.

6. Струков Б.А., Леванюк А.П. Физические основы сегнетоэлектрических явлений в кристаллах. – М.: Наука, 1995. – 304 с.

7. Струков Б.А., Якушин Е.Д. Влияние крупномасштабных неоднородностей на фазовый переход в сегнетоэлектрических монокристаллах триглицинсульфата // Письма в ЖЭТФ. – 1978. – Т. 28, Вып.1. – С. 16.

8. Altukhov V.I., Strukov B.A. The critical phonon scattering and peculiarities of the thermal conductivity in ferroelectrics // Cond. Matt. Phys. – 2002. – Vol. 5, № 4. –P. 769–776.

9. Gonsalo J.A. // Phys. Rev. – 1968. – Vol. 144. – P. 662.

10. Imai K. // J.Phys.Soc. Jap. – 1977. – Vol. 43. – P. 1320.

11. Strukov B.A., Belov A.A. Heat transport properties of ferroelectrics and related materials // Phase transition. – 1994. – Vol. 51. – P. 175.

12. Strukov B.A., Belov A.A. and Altukhov V.I. Study of phonon scattering processes in displacive ferroelectrics by means of heat conductivity measurement // Ferroelectrics. – 1994. – Vol. 9. – Р. 25–30.

13. Strukov B.A., Taraskin S.A., Fedorikhin V.A., Minaeva K.A. // J. Phys.Soc. Jap. – 1980. – Vol. 49. – P. 7.

Около температуры структурного фазового перехода Тk = 322,16 °К одноосные кристаллы триглицинсульфата (ТГС-(NH2CH2COOH)3)H2SO4) обладают уникальными свойствами. Они хорошо исследованы и являются классическими модельными объектами феноменологической теории фазовых переходов второго рода, в рамках которой удается получить качественное объяснение аномального поведения лямбда-типа около Тk диэлектрической проницаемости ε22(Т) [9], теплоемкости Ср(Т) [13], упругих модулей k(T) [6], коэффициента теплового расширения К22(Т) [10], коэффициенты теплопроводности λ(Т) [3, 5, 7–8, 11–12]. Аномальное поведение этих характеристик связывают с наличием флуктуационных эффектов в широкой области температур около Тk. С другой стороны, в одноосных сегнетоэлектриках имеет место относительное подавление флуктуаций поляризации дальнодействующими (кулоновскими) силами [6, 7], что приводит к расширению (по сравнению с многослойными сегнетоэлектриками и фазовыми переходами неэлектрической природы) области применимости термодинамической теории Ландау–Гинзбурга. В итоге сужается область температур (DTL ≤ 0,2÷0,3 °К) около Тk, в которой наблюдаются критические аномалии в поведении термодинамических характеристик этих кристаллов и расширяется область применимости термодинамической теории. При этом в совершенных кристаллах ТГС (температура Дебая q = 1900 °K) температурная зависимость диэлектрической проницаемости вдоль полярной оси ε22 изменяется от температуры по закону Кюри – Вейсса, теплоемкость испытывает скачок на величину αТ/(2β) (α и β – коэффициенты разложения термодинамического потенциала Φ(T, η) по параметру порядка η), компоненты тензера коэффициента теплового расширения К22(Т) испытывают скачок ΔК22(Т) = 17÷20(10–5К–1) вдоль оси симметрии. Несмотря на качественное объяснение этих эффектов в рамках феноменологической теории, численные расчеты аномалий этих характеристик в широкой области температур и около Тk в рамках модели мягкой моды до сих пор не проводились. Тогда как такие расчеты позволяют уточнить модель поведения аномалий и определить ряд важных параметров теории.

В настоящей работе с учетом представлений о роли мягкой моды ωМ(Т) [1, 2, 12, 4] в структурном фазовом переходе предложена микроскопическая модель, проведены расчеты и с единых позиций ωМ(Т) объясняется температурное поведение диэлектрической проницаемости ε22, теплоемкости и коэффициента теплового расширения К22(Т). Результаты расчётов сопоставляются с данными опытов.

Диэлектрическая проницаемость вдоль полярной оси кристалла ТГС

Как видно из рис. 1, изменение ε-122(Т) с температурой характерно для поведения типичной модели мягкой моды. В общем случае статическая восприимчивость обратно пропорциональна квадрату мягкой моды [2]:

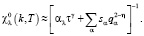(1)

Здесь t = (Т/Тс – 1); g = v(2 – h) – критический индекс восприимчивости; v – критический индекс корреляционной длины  x; h – малый критический индекс; al – коэффициент в разложении термодинамического потенциала по параметру порядка. Дисперсия мягкой моды при q = k – kc → 0 определяется коэффициентами sa через компоненты корреляционной длины xa в виде sa = (xa/x)2–h. Для анизотропного спектра sa могут значительно различаться для направлений a в пространстве обратной решетки. В области температур, где корреляционные эффекты значительны и изотропны, модель мягкой моды можно представить в более простом виде (g = 1, v =1/2, h = 0) [1, 2]:

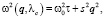(2)

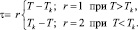(3)

Здесь 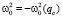– неустойчивая гармоническая частота, дисперсия s при q → 0 порядка 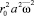, – характерная ширина фононной зоны, r0 – эффективный радиус взаимодействия, a – постоянная решетки. Таким образом, с учетом перенормировки частоты фононов D(w0) для обратной диэлектрической статической восприимчивости получаем

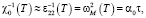
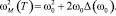(4)

Поведение обратной диэлектрической проницаемости при значениях α0 = 30 К–1 представлено на рис. 1. В низкосимметричной фазе при Т < Тk можно также добиться полного согласия с экспериментом, если использовать значения α0 = 35 К–1. Такое увеличение α0 возможно вследствие его перенормировки в низкосимметричной фазе.

,

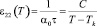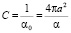, при T > Tk. (5)

Результаты вычислений обратной диэлектрической проницаемости ε–122(ΔТ) для ТГС по (3) – (4) хорошо согласуются с экспериментом [6, 9].

Теплоемкость ТГС в области 200–360 °К

Скачок теплоемкости DCp = aT/(2b) составляет 20÷22 кал/(моль К), при Тk = 322 К (рис. 2). Это превышение в точке Тk над стандартной теплоемкостью кристалла по теории Дебая:

Рис. 2. Температурная зависимость теплоемкости кристалла ТГС: точки – эксперимент [13]; сплошные линии – расчет по формулам (6), (7)

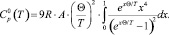(6)

При этом, согласно термодинамической теории, поведение DCp в области 200–322 °К (Т < Tk) имеет вид [6]:

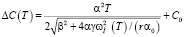, (7)

где С0 = 23 кал/(моль К) связано со значениями теплоемкости на границах расчетной области. Расчеты по формулам (5) и (6) с параметрами R = 1,988 кал/(моль К), А = 4,68, Θ = 190 K дают хорошее согласие с данными опытов (рис. 2). Расчетные значения теплоемкости несколько превышают (на 3–5 %) соответствующие экспериментальные значения. Этот разрыв увеличивается по мере уменьшения температуры вследствие более высокой скорости их изменения при Т → 0, и по-видимому, связан с использованными в феноменологическом подходе определениями DC(Т).

Коэффициент теплового расширения К22(Т) кристалла ТГС вдоль оси 2

Коэффициент К22(Т) вдоль оси 2 около Тk испытывает скачок в точке фазового перехода Тk подобно скачку теплоемкости (рис. 3). При T < Тk коэффициент теплового расширения кристалла ТГС имеет отрицательные значения К0. Кроме того, в непосредственной близости к точке фазового перехода Тk скачок К22(Т) испытывает дополнительное увеличение «сверх изменения», обусловленного теорией Ландау. Это изменение связано, по-видимому, с флуктуациями параметра порядка, и возможно, с особенностью термодинамического потенциала в точке T = Тk [6]. Коэффициент теплового расширения в кристалле без фазового перехода можно, согласно [3], представить в виде К22(Т) = В0∙Cp(Т), где В0 – величина, связанная с постоянной Гринайзена. Изменение коэффициента теплового расширения с температурой связано с частотой мягкой моды 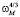, при T < Тk и 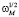, при T > Тk. Тогда К22(Т) можно представить в виде [3]:

,

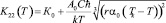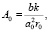при T < Тk, (8)

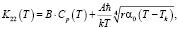
при T > Тk, (9)

где b – коэффициент аргамоничности, a0 – коэффициент упругой связи, k – постоянная Больцмана; a0 = 7,92 K–1, А0С = 0,33∙105, К0 = –13∙105 К–1, при T < Тk и a0 = 5,28 K–1, А = 105, В0 = 4,2 моль/кал, В = 1,9 моль/кал, при T > Тk – постоянные, определяемые граничными условиями модели. В области T > Тk коэффициент теплового расширения К22(Т) резко выходит на насыщение, достигая значения 5·(10–5 К–1). Результаты вычислений по формулам (8), (9) с учетом скачка ΔК22 при Т = Тk в целом согласуются с данными опытов (рис. 3).

Рис. 3. Температурная зависимость коэффициента теплового расширения вдоль оси 2: точки – эксперимент [10]; пунктир – К22(Т) – в кристалле без фазового перехода; сплошные линии – расчет по формулам (8), (9)

Выводы

В работе проведены численные расчеты, и с единых позиций мягкой моды дано объяснение аномальному температурному поведению диэлектрической проницаемости вдоль полярной оси, теплоемкости в широкой области температур и вблизи Тk, а также коэффициента теплового расширения кристалла ТГС вдоль оси 2. Результаты расчетов обратной диэлектрической проницаемости ε-122(Т) соответствуют температурному поведению мягкой моды около Тk и обеспечивают зависимость диэлектрической проницаемости от температуры по закону Кюри – Вейсса. Несмотря на использование при расчете теплоемкости приближения Дебая, с учетом ее скачка по теории Ландау около Тk, рассчитанные значения теплоемкости в широком интервале температур хорошо согласуются с данными опытов. Дополнительный скачок теплового расширения К22(Т) «сверх» предсказываемого феноменологической теорией объясняется флуктуациями параметра порядка и подобран исходя из наилучшего согласия теории с экспериментом [6, 10]. Таким образом, аномальное температурное поведение ε22(Т), Ср(Т) и К22(Т) в ТГС не только находят свое качественное объяснение в рамках феноменологической теории, но и согласуются с результатами численных расчетов с учетом микроскопической модели мягкой моды. В ходе расчетов получены значения ряда важнейших параметров теории. Данные численных расчетов аномального температурного поведения диэлектрической проницаемости вдоль полярной оси, теплоемкости в широком интервале температур и коэффициента теплового расширения хорошо согласуются с соответствующими экспериментами.

Янукян Э.Г., д.ф.-м.н., профессор, профессор кафедры физико-математических дисциплин, декан инженерного факультета филиала СКФУ в г. Пятигорске, г. Пятигорск;

Чернобабов А.И., д.ф.-м.н., профессор, профессор кафедры физико-математических дисциплин филиала СКФУ в г. Пятигорске, г. Пятигорск.

Работа поступила в редакцию 19.02.2015.

Библиографическая ссылка