В результате многолетних исследований по созданию прецизионных микромеханических датчиков ускорения было предложено множество конструктивных решений, среди которых наибольшее распространение получили акселерометры с емкостным преобразованием перемещения инерционной массы. Датчики такого типа преобразования имеют достаточно высокую точность и широкий диапазон измерения до 105 g [4]. Существует класс микромеханических акселерометров, принципиально отличающихся по принципу измерения ускорения от традиционных. Датчики такого класса, основанные на эффекте изменения резонансной частоты осциллятора в зависимости от действующего ускорения, называются резонаторными. В силу особенностей функционирования, акселерометры резонаторного типа могут применяться в высокочувствительных сейсмоприемниках и гравитационных градиентометрах, где необходима точность измерения виброускорений в пределах 10–6–10–9 g [2, 3].
Проблемы создания высокочувствительных микромеханических датчиков в первую очередь связывают с их сверхмалыми массогабаритными характеристиками, а также технологией изготовления. Несмотря на довольно большие перспективы развития акселерометров резонаторного типа, последние подвержены существенному влиянию внешних возмущающих воздействий. Основным параметром, определяющим рабочий режим прибора, является собственная частота его чувствительных элементов, которая зависит от множества факторов, влияющих на работу датчика. В качестве возмущающих воздействий исследовались деформации, возникающие в резонаторах вследствие действия линейных ускорений и моментов на инерционную массу. Целью исследования является определение степени влияния вида деформации на собственные частоты резонаторного микроакселерометра.
Принцип работы резонаторных микроакселерометров основан на измерении отклонения собственных частот чувствительных резонаторов, вызванных упругими деформациями, возникающими вследствие смещения инерционной массы под действием ускорения. В качестве объекта исследования был выбран одноосный резонаторный микроакселерометр, имеющий два чувствительных резонатора, оси чувствительности которых расположены вдоль оси Х (рис. 1).
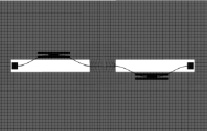
Микроакселерометр содержит инерционную массу 1, соединенную с опорами 2 через упругие перемычки 3. Элементы 4 представляют собой гребенчатые структуры электростатической системы возбуждения-съема информации. Упругие перемычки 3 вместе с гребенчатыми структурами 4 образуют чувствительные резонаторы. Рабочий режим микроакселерометра характеризуется наличием колебаний резонаторов в плоскости XY микроструктуры с частотой их собственных колебаний. Форма колебаний резонаторов в рабочем режиме соответствует шестой и седьмой модам, которые имеют следующий вид (рис. 2).
Датчик способен измерять составляющую линейного ускорения вдоль оси Х. Проекции абсолютного ускорения на две другие оси Y и Z являются паразитными и вносят определенную долю погрешности в выходной сигнал. Кроме того, погрешности возникают вследствие действия вредных моментов вокруг всех трех осей X, Y и Z.
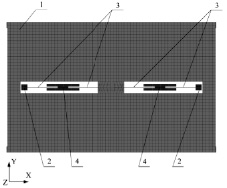
Рис. 1. Модель одноосного резонаторного микроакселерометра
Для определения степени влияния вредных боковых ускорений и моментов, действующих на инерционную массу, были использованы методы конечно-элементного анализа и теории колебаний.
Для удобства анализа акселерометра методами математического аппарата его структура представляется в виде системы с сосредоточенными параметрами, где упругие элементы обладают конечной жесткостью, а инерционная масса рассматривается как недеформируемое твердое тело, при этом движение инерционной массы осуществляется по шести степеням свободы, а опоры считаются неподвижными относительно корпуса датчика.
а 
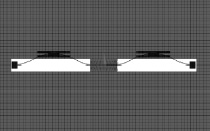б
Рис. 2. Рабочие формы колебаний резонаторов: а – шестая мода; б – седьмая мода
Для определения собственной частоты упруго-напряженного резонатора воспользуемся теорией тонких стержней. Колебания тонкого стержня можно описать одномерным волновым уравнением [5]
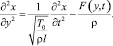(1)
Неоднородное уравнение описывает малые поперечные колебания тонкого стержня, на который действуют поперечные силы F(y, t), представляющие собой гармоническое воздействие. Для стержня конечной длины, закрепленного по концам, граничные условия определяются как
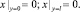
Решением уравнения (1) при данных граничных условиях является гармоническая функция
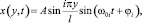
где i = 1, 2, 3…
Данная функция определяет положение каждого элементарного участка стержня, колеблющегося с амплитудой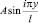 
по координате y в каждый момент времени t. Здесь ω0i – циклическая частота i-й моды свободных колебаний элементарного участка стержня.
Циклическая частота свободных колебаний стержня, жестко закрепленного по концам, определяется выражением [6]
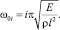
Отклонения инерционной массы от положения равновесия, вызванные силами инерции, вызывают деформации продольного растяжения, сжатия, кручения и изгиба резонаторов, что в свою очередь оказывает влияние на их собственные частоты.
Уравнение колебаний стержня в плоскости XY, нагруженного продольными силами, имеет вид [1]
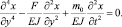
Решение данного уравнения, соответствующее колебаниям резонатора в плоскости XY имеет вид
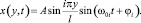
Подставляя полученное уравнение в предыдущее, получаем
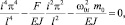
откуда
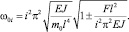(2)
Последнее уравнение соответствует i-й форме колебаний стержня в плоскости XY. Дополнительный множитель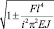 
отражает влияние продольной силы F, действующей со стороны инерционной массы, причем знак минус подкоренного выражения соответствует сжимающей нагрузке, а плюс – растягивающей. Критическая нагрузка, при которой стержень перестает оказывать сопротивление действующей поперечной нагрузки, определяется выражением
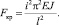
При достижении продольной силы критического значения собственная частота стержня обращается в нуль [1].
Численный расчет собственных частот резонаторов, соответствующих шестой и седьмой модам, в зависимости от вида деформаций, проводился в системе конечно-элементного анализа ANSYS. При анализе необходимо учитывать как поступательное, так и угловое смещение инерционной массы, поэтому в качестве эквивалентов сил инерции, оказывающих воздействие на инерционную массу при действии ускорений и моментов, прикладывались силы и моменты по шести степеням свободы.
Примеры деформированной микроструктуры акселерометра приведены на рис. 3, 4.
Зависимости собственных частот шестой и седьмой мод колебаний резонаторов от величины и типа нагрузки, действующей со стороны инерционной массы, приведены на рис. 5.
Исходя из особенностей конструкции микроакселерометра, полезной является продольная нагрузка Fx, которая оказывает наибольшее воздействие на собственные частоты обоих резонаторов. Вследствие этого чувствительность прибора непосредственно зависит от крутизны данной характеристики.
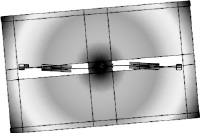
Рис. 4. Момент вокруг оси Z
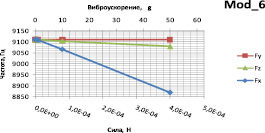
Рис. 5. Зависимость частоты шестой моды резонатора от усилия
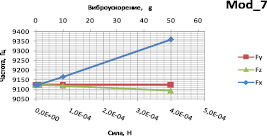
Рис. 6. Зависимость частоты седьмой моды резонатора от усилия
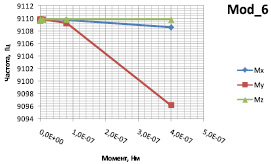
Рис. 7. Зависимость частоты шестой моды резонатора от момента
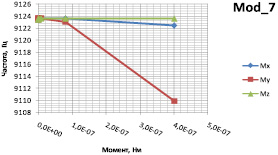
Рис. 8. Зависимость частоты седьмой моды резонатора от момента
При действии силы вдоль осей X, Y и Z наблюдается линейная зависимость собственной частоты от приложенного усилия, причем наибольшее влияние оказывает продольное усилие в резонаторах. Повышение чувствительности к продольным нагрузкам достигается путем варьирования геометрических размеров резонатора согласно выражению (2), при этом крутизна характеристики увеличивается. Боковые ускорения в меньшей степени влияют на собственные частоты, однако необходимо их максимальное снижение. Это достигается внедрением в конструкцию дополнительных упругих перемычек, повышающих жесткость в направлениях Y и Z. Влияние вредных моментов так же можно снизить при помощи внедрения дополнительных элементов жесткости и промежуточных рамок.
Работа выполнена в Томском политехническом университете при финансовой поддержке Минобрнауки, ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 годы», Соглашение № 14.575.21.0068, уникальный идентификатор RFMEFI57514X0068.
Рецензенты::
Бориков В.Н., д.т.н., профессор, директор «Институт неразрушающего контроля», заведующий кафедрой «Точное приборостроение», ФГОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск;
Дмитриев В.С., д.т.н., профессор кафедры «Точное приборостроение», ФГОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.
Работа поступила в редакцию 01.04.2015.
Библиографическая ссылка
Вторушин С.Е., Нестеренко Т.Г. МОДАЛЬНЫЙ АНАЛИЗ ДЕФОРМИРОВАННОЙ МИКРОСТРУКТУРЫ РЕЗОНАТОРНОГО МИКРОМЕХАНИЧЕСКОГО АКСЕЛЕРОМЕТРА // Фундаментальные исследования. – 2015. – № 2-12. – С. 2553-2557;URL: https://fundamental-research.ru/ru/article/view?id=37521 (дата обращения: 19.04.2024).