Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Нестеренко Т.Г. 1

---

1 ФГАОУ ВО «Национальный исследовательский Томский политехнический университет»

Проведён анализ влияния температуры на микроэлектромеханические системы. Микроакселерометры, микрогироскопы и микрорезонаторы могут быть представлены обобщённой схемой осциллятора с электростатическими и упругими силами. При изменении температуры изменяются линейные размеры конструкции, изменяется модуль упругости кремния, в конструкции возникают внутренние механические напряжения, нарушается геометрическая форма. Это приводит к изменению частотных свойств чувствительного элемента. Методом конечных элементов проведён модальный и температурный анализ нескольких конструкций осцилляторов, для которых определены формы колебаний, имеющие наименьшую и наибольшую чувствительность к изменению температуры. Осцилляторы с наибольшей температурной чувствительностью могут использоваться в качестве встроенных в микросистему датчиков температуры. Для микрогироскопов, микроакселерометров и микрорезонаторов выбраны формы колебаний, имеющие наименьшую температурную чувствительность.

Статья в формате PDF

1416 KB

микрогироскоп

микроакселерометр

микрорезонатор

осциллятор

модальный и температурный анализы

формы колебаний

1. Евстигнеев М.И., Смирнова М.Ф., Унтилов А.А. Анализ механических, электрических и тепловых характеристик при проектировании микромеханического гироскопа // Навигация и управление движением: сб. докладов III научно-технической конференции молодых ученых 12–14 марта 2002 г.). – СПб.: ЦНИИ «Электроприбор», 2002. – С. 142–148.

2. Нестеренко Т.Г., Пересветов М.В., Коледа А.Н., Колчужин В.А. Электродная структура микромеханического гироскопа // Промышленные АСУ и контроллеры. – 2012. – № 7. – C. 62–66.

3. Попова И.В., Лестев А.М., Семенов А.А., Пятышев Е.Н., Лурье М.С., Иванов В.А., Шабров А.А. Микромеханические датчики и системы, практические результаты и перспективы развития // ХII Международная конференция по интегрированным навигационным системам.  – СПб., 2005. – С. 262–267.

4. Fang J.C., Li J.L., Sheng W.J. Improved temperature error model of silicon MEMS gyroscope with inside frame driving // Beijing Univ. Aeronaut. Astronaut. – 2006. – P. 1277–1280.

5. Dunzhu Xia. Microgyroscope Temperature Effects and Compensation-Control Methods / Shuling Chen, Shourong Wang and Hongsheng Li // Sensors Journal. – 2009. – № 9. – Р. 8349–8376.

6. Sheng-Ren Chiu. An Integrated Thermal Compensation System for MEMS Inertial Sensors / Li-Tao Teng, Jen-Wei Chao, Chung-Yang Sue, Chih-Hsiou Lin, Hong-Ren Chen and Yan-Kuin Su. – Sensors Journal. – 2014. – № 14. – Р. 4290–4311.

Микроэлектромеханические системы (МЭМС) – одно из наиболее перспективных направлений в современной электронике. Технология МЭМС позволяет методами, близкими к технологии производства микросхем, получать в интегральном процессе системы с электрическими, электронными, механическими, оптическими и электрохимическими свойствами и размерами, сравнимыми с обычными интегральными схемами. МЭМС-устройства находят широчайшее применение в потребительской и специальной электронике, системах безопасности автомобилей, навигации, медицине, средствах мониторинга и неразрушающего контроля и многих других областях.

Проникновение датчиков во все сферы жизни во многом произошло благодаря технологии МЭМС, которая наконец стала массовой и недорогой. Применение решений с одновременной обработкой показаний датчиков различного типа позволяет улучшать устройства потребительской электроники.

Бурное развитие МЭМС-датчиков обусловлено их существенными достоинствами [1, 2], такими как малый разброс параметров в пределах изделия; высокая технологичность и повторяемость; микроминиатюрность; высокая функциональность; высокая надежность и стойкость к внешним воздействиям из-за их малых габаритов; низкая стоимость.

Наиболее распространёнными микроэлектромеханическими системами являются микроакселерометры, микрогироскопы и микрорезонаторы. Для производства микроакселерометров и микрогироскопов используют идентичные кремниевые структуры, разница заключается в управлении. Микрорезонаторы могут применяться в качестве задающего элемента в генераторах схемотехники для формирования колебаний со стабильной частотой.

Температурный анализ

Микроэлектромеханические датчики должны работать в широком температурном диапазоне. Под влиянием температуры возникают изменения линейных размеров конструкции, изменяется модуль упругости кремния, в конструкции возникают внутренние механические напряжения, нарушается геометрическая форма. Всё это повлечет за собой изменение частотных свойств МЭМС.

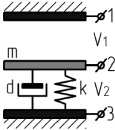
Микроакселерометры, микрогироскопы и микрорезонаторы представляют собой колебательные системы (осцилляторы) [4] с электростатическими силами, эквивалентная обобщённая схема которых изображена на рис. 1.

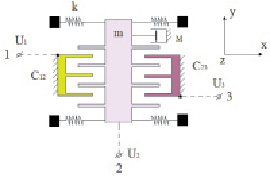 а б

Рис. 1. Эквивалентные схемы сенсоров микросистемы: а – осциллятор с планарными электродами; б – осциллятор с гребенчатыми электродами

Динамическое уравнение, описывающее осциллятор, возбуждаемый электростатическими силами, в модальных координатах для i-й моды, имеет вид

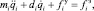(1)

где mi – модальная масса; di – модальный коэффициент демпфирования; qi – модальные амплитуды (смещение i-моды).

При приложении между электродами электрического напряжения возникают электростатическая сила притяжения 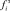и компенсирующая её сила упругости 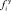. Сила упругости определяется как

,

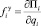где Пi – энергия деформации упругого элемента системы. Электростатическая сила вычисляется как производная от функции ёмкости

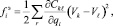
где Vk, Vℓ – соответственно электрические потенциалы на обкладках k и ℓ; r = n(n – 1)/2 – число емкостей n-электродной системы.

При использовании осциллятора в качестве датчика температуры его характеристики должны максимально изменяться при изменении температуры. При использовании же осциллятора в качестве сенсора гироскопа, акселерометра, задающего элемента генератора его характеристики должны минимально реагировать на изменение температуры [4, 5, 6].

Поэтому температурный анализ является важным типом анализа с целью выявления собственных частот, на которые оказывает наибольшее влияние данный тип нагрузки.

Разработка и исследование осцилляторов связаны с решением задач математической физики, к которым относятся задачи теплопроводности, задачи о деформациях твердых тел и взаимосвязанные задачи. Нахождение точного аналитического решения возможно лишь для весьма ограниченного круга одномерных задач и при использовании целого ряда допущений.

С большей точностью анализ систем с распределёнными параметрами, к которым относятся микромеханические конструкции, осуществляется методами конечных элементов с применением компьютерных методов расчёта.

На первом этапе для оценки динамического поведения осциллятора применяется модальный анализ. Рассмотрим МЭМС-осцилляторы различных форм, которые могут быть использованы для моделирования сенсоров датчиков (микрогироскопов, микроакселерометров, микрорезонаторов, датчиков температуры).

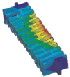
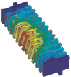
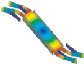
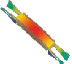
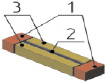
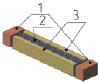
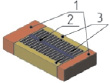
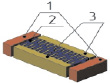
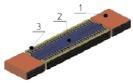
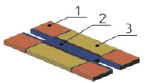
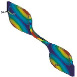
Разработка конструкций и модальный анализ микроосцилляторов производились в Аnsys/Multiphysics. Геометрические размеры микроосцилляторов подбирались таким образом, чтобы частоты первых форм их колебаний были близки друг к другу. В таблице 1 представлены различные типы микроосцилляторов, каждый из которых состоит из подвижной массы 2, закрепленной в неподвижном основании 1. Возбуждение колебаний подвижной массы производится за счет электростатического привода 3, который может быть гребенчатым (резонаторы 2, 3, 4 и 5 типа) или планарным (первый тип осциллятора).

Построение сетки конечных элементов производится на основе 2D профиля, затем вытягивается в объеме на нужную высоту 50 мкм методом протягивания (sweep), материал осцилляторов – монокристаллический кремний. Решение производилось для первых десяти собственных частот колебаний. В табл. 2–7 представлены результаты расчетов для шести типов микроосцилляторов.

Таблица 1

Типы конструкций микроосцилляторов

Таблица 2

Формы колебаний первого осциллятора

Таблица 3

Формы колебаний второго осциллятора

Таблица 4

Формы колебаний третьего осциллятора

Таблица 5

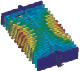
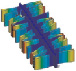
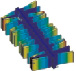
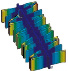
Формы колебаний четвертого осциллятора

Таблица 6

Формы колебаний пятого осциллятора

Таблица 7

Формы колебаний шестого осциллятора

В осцилляторе микроакселерометра и микрогироскопа рабочей является первая форма колебаний [3], частоты всех остальных форм должны быть больше, что и было выполнено при создании их геометрии. Результаты температурного анализа передаются в частотный анализ и определяются частоты десяти форм колебаний осцилляторов при заданных температурах окружающей среды.

На рис. 2–7 представлены результаты температурного анализа осцилляторов – относительные изменения частоты для каждой моды колебаний.

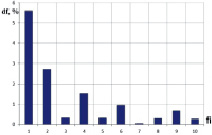
Рис. 2. Относительные изменения частот первого осциллятора

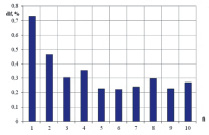
Рис. 3. Относительные изменения частот второго осциллятора

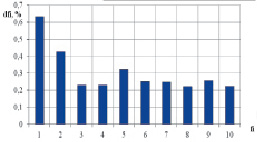
Рис. 4. Относительные изменения частот третьего осциллятора

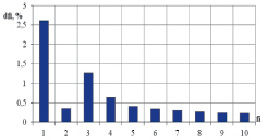
Рис. 5. Относительные изменения частот четвертого осциллятора

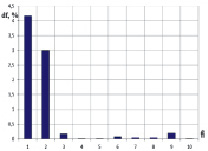
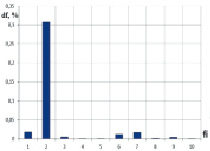
Рис. 7. Относительные изменения частот шестого осциллятора

Заключение и выводы

Для первого осциллятора наибольшей температурной чувствительностью обладает первая форма его колебаний, которая является рабочей в режиме датчика температуры. Седьмая форма колебаний осциллятора имеет минимальную чувствительность к изменению температуры и является рабочей при использовании осциллятора в генераторах.

Наименее чувствительны к изменению температуры 2, 3 и 6-й осцилляторы, которые могут использоваться в качестве сенсоров микрогироскопов, микроакселерометров и микрогироскопов. Наибольшую чувствительность к изменению температуры имеют осцилляторы первого и пятого типов, которые будут использоваться в качестве датчика температуры в многокомпонентной системе (рис. 8, 9).

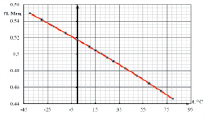
Рис. 8. Температурная зависимость частоты f1 осциллятора первого типа

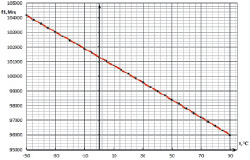
Рис. 9. Температурная зависимость частоты f1 осциллятора пятого типа

Зависимость изменения частоты первой формы колебаний осцилляторов датчиков температуры имеет линейный характер.

Работа выполнена в Томском политехническом университете при финансовой поддержке Минобрнауки России, ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 годы», Соглашение № 14.575.21.0068, уникальный идентификатор соглашения RFMEFI57514X0068.

Рецензенты::

Дмитриев В.С., д.т.н., профессор, Национальный исследовательский Томский политехнический университет, г. Томск;

Бориков В.Н., д.т.н., директор Института неразрушающего контроля, Национальный исследовательский Томский политехнический университет, г. Томск.

Работа поступила в редакцию 01.04.2015.

Библиографическая ссылка